はじめに

統計的因果推論における1つの達成目標として「介入を行った場合には行わなかった場合と比較してどの程度結果（アウトカム）が変わったのか」という因果的な疑問に対し、定量的に答えることが挙げられるかと思います。以前のコラムでは、こういった因果効果を数学的・統計学的に議論していくために潜在アウトカムという考え方を導入し、その値を推定していくために重要ないくつかの仮定について紹介を行いました。この因果効果の推定の手法には様々なものがありますが、次回以降のコラムで紹介をする交絡調整に基づく因果効果の推定手法 (e.g., 回帰、層別化、傾向スコアを用いた手法）では、興味のある因果効果の推定値をバイアスなく得るためには、交絡や選択バイアスの調整に必要な全ての変数が完全に特定・測定されているという仮定が成立している必要があります。この仮定はデータからその成立を検証することはできず、もしもいずれかが成立しない場合には得られる推定値にはバイアスが含まれ、いわゆる残差交絡 (redidual confounding) が存在する状況となります。現実的に仮定が全て厳密に成立するケースというのは比較的稀ですので、そのような意味では大部分の研究結果（特に観察研究）・解析結果には一定のバイアスが含まれているとみることもできるかと思います。ただし交絡調整に基づく手法がダメだと言っているわけではなく、調整が不完全ながらもバイアスを軽減することは十分に意義があり、また最終的に結果に含まれるであろうバイアスの大きさとその方向（過大評価 or 過小評価）を議論することが重要かと思います。

今回のコラムでは、操作変数法（instrumental variable methods, IV methods）という因果効果の推定手法について紹介と解説を行っていきます。この推定手法は、操作変数 (instrumental variable, instrument) と呼ばれるいくつかの条件を満たす特殊な変数を利用することで因果効果の推定を行う手法になります。医学分野では、先行研究の結果（e.g., 医学的な知見）から交絡因子となりうる変数の特定・測定が比較的容易であることから先ほど言及した交絡調整に基づく推定手法が用いられるケースが比較的多いですが、経済学や社会科学といった分野ではそもそもの特定が出来なかったり、仮に交絡因子であろうと見込んだ場合であってもそれを測定することができないケースが非常に多く存在します。そのため交絡調整に基づかない手法である操作変数法というのは経済学や社会科学において、特にその理論が発展してきたという歴史的な背景があります。なお詳細については後述しますが、操作変数法は交絡因子の測定を必要としないというメリットもある一方、いくつかの検証不可能な仮定に基づく手法です。したがって、解析を行う研究・データにおいて因果効果の推定のために要求される仮定の成立を認めることがどの程度妥当であるかの議論が他の手法と同様に必要であることにご注意ください。

 

操作変数の3条件

操作変数法では、ある介入AのアウトカムYに対する因果効果を推定するために以下の3つの条件を満たす変数Zを利用します。この変数Zは操作変数 (instrumental variable, instrument) と呼ばれます。

• 操作変数の3条件 (Theree instrumental conditions) 

1. 1. Z is associated with A
      • ZはAと関連する
   2. Z does not affect Y except through its potential effect on Y
      • ZはYに対してAを介した以外の効果を持たない
   3. Z and Y do not share cause
      • ZとYは共通原因を持たない

次に、これらの条件より詳細に考えていくために変数間の関係が以下のDAGで表現される二重盲検ランダム化実験 (randomized experiment)^※1 を考えます。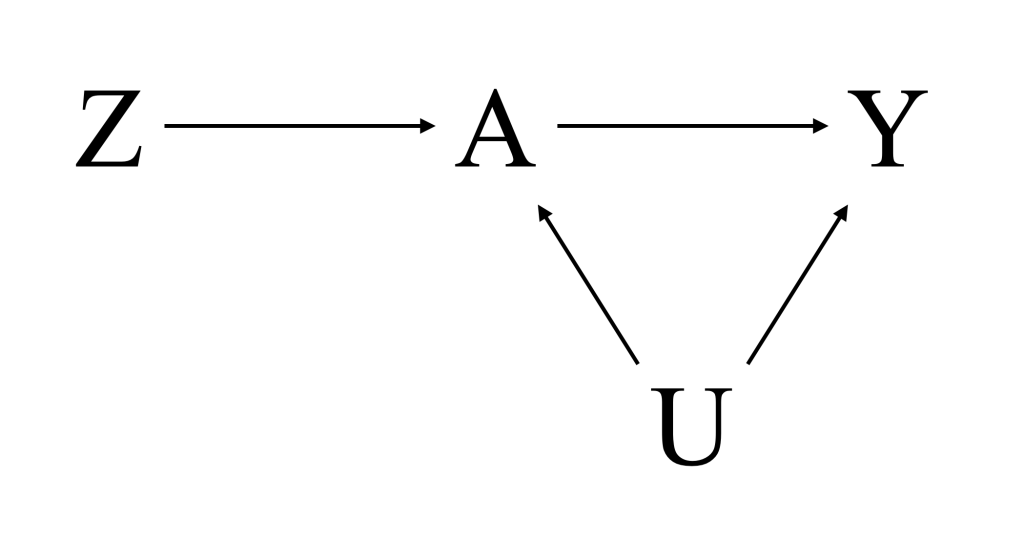

• Z: ランダム割付変数（1：介入群、0：対照群）
• A: 実際に受けた介入（1：介入あり、0：介入なし）
• Y: アウトカム
• U: AとYに影響を及ぼす全ての共変量、AとYのcommon cause（未測定の共変量を含む）

操作変数の3条件はこのDAGにおいては以下のことを意味しています。

ここで、なぜ変数Z（介入群 / 対照群のいずれに割り振りされるか）と変数A（実際の介入）を区別しているかについてですが、これはノンコンプライアンス（不遵守）^※2と呼ばれる問題が発生している状況を想定しているためです。これは研究実施者による各被験者への介入の割付と実際に行われる介入がなんらかの理由によって異なるというものです。例えば上記の介入Aがワクチン接種であった場合、仮にワクチン接種を受ける群（介入群）に割付られてもその接種を拒否する個人が存在したり（Z=1かつA=0）、反対にワクチン接種を受けない群（対照群）に割付られても研究外で個人的に接種を行う被験者（Z=0かつA=1）が存在したりする可能性があります。このようなノンコンプライアンスは、たいていの介入に対して考えることができ、今回の状況設定はそのような一般的な状況を反映した結果となっています。

※1　どの被験者が介入群 / 対照群に割付られているかをわからなくさせることを盲検化といい、割付側（医師など）と被験者の両者に対して盲検化を行うことを二重盲検化という
※2　コンプライアンスではなくアドヒアランスという言葉が用いられる場合もある

 

1. Z is associated with A

1つ目の条件はZとAが関連していること（相関が0ではない） 、もしくはZとAの非独立性です。この条件はしばしばrelevance conditionと呼ばれ、操作変数の3条件の中で唯一検証することが可能な仮定です。なおこの条件については、関連が存在しているかしていないかという二分的な議論だけではなく、関連が認められる場合にはどの程度ZとAが関連しているのかということ定量的な評価が、操作変数法による因果効果の推定のために重要なポイントとなります。その程度が弱い（介入Aとの相関が弱い）操作変数Zは、弱操作変数 (weak istrument) と呼ばれ、弱操作変数を因果効果の推定のために利用した場合には得られる因果効果の推定値の分散および信頼区間がかなり大きくなってしまうという問題が発生します。弱操作変数は、Hernan and Robins, 2022 では以下がその定義として挙げられており、操作変数法において分散が小さい推定値を得るためには基準に当てはまらない強い操作変数を探す必要があります。

• 弱操作変数の定義
  1. ZとAの関連 (E[A|Z=1]-E[A|A=0]) の真値が小さい
  2. 観察されたZとAの関連性に関連するF統計量が10未満

また操作変数は、ZがAに直接的に効果を与えているのか、それとも直接効果を与えている変数を介して関連しているかによって次の2つに分類することが可能です。

• causal instruments
  • 介入Aに対し直接的に因果効果を持つ
  • 一般には操作変数Zは介入Aと関連していれば良いため比較的特殊な例として扱われることが多い
  • 変数Zがcausal instrumentであるDAGの例

• surrogate (proxy) instrument
  • 介入Aに対し直接的に因果効果を持つ変数Uzを介して介入Aと関連する
  • 変数Zがsurrogate instrumentであるDAGの例
    左）ZとAの間に未測定であるcausal instrument Uzがcommon causeとして存在しており、関連が発生
    右）ZとAのcommon effectとしてcausal instrument Uzが存在しており、通常ZからAへのパスは閉じているがUzで条件付けを行うことによってパスが開き関連が発生^※1

操作変数をcausal instrumentとsurrogate instrumentに区別する理由についてですが、これは推定結果の解釈や追加の仮定を議論する際に必要となるためです。詳細は次回のコラムで扱います。

※1　交絡に関するコラムを参照

 

2. Z does not affect Y except through its potential effect on A

2つ目の条件はZはYに対しAを介した潜在的な効果以外の効果を持たないこと、すなわちZの直接効果は存在せずAを介した間接効果のみ存在することです。特に経済学の分野ではexclusion restriction（除外制約）として知られており、DAG上ではZからYへの直接的な矢印が存在しないことを意味します。また、正確にはこの条件には次の個人レベルと集団レベルの2つのバージョンが存在します。

• 個人レベルでの除外制約
  • Y_i^{z, a}=Y_i^{z', a}=Y_i^a for all z, z', all a, all individuals i
• 集団レベル
  • E[Y^{z, a}]=E[Y^{z', a}]

このいずれのバージョンも、二重盲検が行われるランダム化実験においてはその成立が期待されます。これは全ての被験者や被験者と関わりのある割付側全員が割付の結果を知らないのであれば、行動変容等による副次効果が存在しないことが期待されるためです。なお本コラム・シリーズで紹介する解析例に関しては、比較的弱い仮定である集団レベルでの除外制約が成立していれば因果効果の推定を行うことが可能です。

この条件は先ほどのZとAの関連に関する条件とは異なりその成立が検証することができない仮定です。すなわち、因果効果の推定に操作変数法を用いる場合 (i.e., ある変数を操作変数として提案する場合) には、あくまでこの仮定が成立するという想定の下で議論を行っていくこととなり、その妥当性についての議論が必要となります。検証が不可能かということを先ほどのcausal instrumentであるに対して考えてみます。

まず、DAGで表現されるように真には条件が成立している (i.e., Z→Yが存在していない) とします。ここで条件の成立はAを介した間接効果のみ存在するということを意味していますので、一見するとZとYの中間因子であるAで条件付けを行った場合には、ZとYは無相関となることが予想されるかと思います。しかしこの論理は、未測定交絡因子Uの存在によって破綻します。Aは当然ながらZとYの中間因子ですのでAで条件付けを行うとZ←Uz→A→Yというパスは閉じます（条件付けによってこのパス上でのZとYの関連が消える）。ですがAは同時にUzとYのcommon causeでもありるため、条件付けを行わない場合にはZ←Uz→A←U→Yというパスは閉じているのですが、Aで条件付けをおこなってしまうとこのパスが開いてしまうことになり、ZとYの間に関連が生まれてしまいます。よって仮定の成立を検証することはできず、介入とアウトカムの間には常に未測定の交絡因子の存在の可能性を議論していく必要があります。なお、この議論はsurrogate instrumentsに対しても同様です。

 

3. Z and Y do not share cause

3つ目の条件はZとYのcommon causeが存在しないこと、DAG上での表現としてはZとYの両方に矢印が向かう変数が存在しないことになります^※1。この条件は、ZとAとの全てのレベルに対応する潜在アウトカムY^{a, z}が変数Zと独立であるというmarginal exchangeabilityとして表記されることもあり、先ほどの個人レベルでの2つ目の条件と併せて考えると、潜在アウトカムY^aと治療割付変数Zの独立性を意味しています。また共に二値である操作変数と介入に対しては、marginal exchangeabilityよりも強い仮定として以下のjoint exchangeabilityが用いられることもあります。

• marginal exchangeability^※2
  • Y^{a, z} ⊥ Z for all a, z
• joint exchangeability^※2
  • {Y^{a, z};a∈[0, 1], z∈[0, 1]} ⊥ Z for all a, z

marginal exchangeability, joint exchangeabilityの紹介・議論については、以前の交換可能性に関するコラム（補足資料）をご参照ください。また変数Zがcausal instrumentであるための第3の条件はZとYのcommon causeが存在しないことですが、surrogate instrumentに対してはZとYのcommon causeがUzを除いて存在しないと修正される点にご注意ください。なおこの3つ目の条件は、2つ目の条件と同様にその成立が検証することができない仮定です。これは交絡に関する議論と同様にZとYの間に常に未測定の共変量が存在する可能性が常に存在するためです。

※1　仮にcommon causeが存在したとしても測定できていれば、それを調整することによって操作変数法を適用できることがある
※2　⊥は統計学上の独立を意味するものとする

 

 

ランダム化実験における割付変数と操作変数の関係

本コラムの冒頭で紹介したようなランダム化実験における諸変数と操作変数との関係性を考えてみると、二重盲検が行われるランダム化実験においてはランダム割付変数が操作変数の最も有力な候補として挙げられます。これは操作変数の3条件について、それぞれ以下の事項が期待されることからその成立が妥当であると考えることができるためです。

1. Z is associated with A
   • 介入群に割付けられた被験者は実際に介入を受けやすく、かつ対照群に割付けられた被験者は実際に介入を受けない（Z=1であればA=1, Z=0であればA=1となる）傾向が期待される
   • 一部の臨床試験や施策のように、必ず介入群に割付られた場合には対照となる介入が実施されない（or 対照群に割付られた場合には介入が実施されない）ことがデザイン上成立する研究においては特に成立がしやすい
2. Z does not affect Y except through its potential effect on Y
   • 二重盲検が行われる場合には、プラセボ効果やホーソン効果といった行動変容によるアウトカムへの副次効果 (side effect) が取り除かれることが期待されるため、介入による効果（間接効果）のみが存在すると期待される
3. Z and Y do not share cause
   • Zはランダム割付変数である (i.e, 割付は他の変数とは無関係に実施される) ため、無条件でのZとY^aの独立性の成立が期待される

ランダム割付変数は治療割付の意図による効果 (Intention-to-treat effects, ITT effects) を計算する際にしばしば用いられますが、このITT effectsに関する議論は理論的には操作変数法とほぼ同様です。この辺りについてもまた別のコラムでいつか紹介を行います。

 

実際に操作変数として提案された変数の例

さて、ここまで操作変数となるための条件について紹介を行ってきましたが、おそらくここまで読まれた方の大部分は「一体そのような都合のいい変数が存在するのか」という疑問を抱いたかと思います。現実問題として操作変数法の使用が難しいポイントはまさにそこであり、ランダム割付変数が存在するランダム化実験はまだ良いものの、ランダム化が行われない実験研究や観察研究) の場合にはランダム割付変数が存在しないので適切な操作変数を選択することが大変難しくなります。そのため操作変数法が適用できないケースや、得られた結果に対する批評が寄せられることも珍しくありません。ただ操作変数法の概要を知っておくことにデメリットはありませんし、より現実的な発展的内容にもつながるため、いくつかの研究で実際に操作変数ではないかと提案された変数を紹介をします。

• Genetic factor（遺伝要因）
  • 一部のgenetic variant（遺伝的変異）
  • アルコールの接種が冠状動脈性心疾患（CHD）リスクに対して与える効果の推定時の、アルコール代謝に関連する多型（polymorphism） (e.g., アジア人の集団におけるALDH2)
  • 遺伝的変異を用いた操作変数法による推定を介した大規模な観察データからの因果推論は、メンデルランダム化（Mendelian randomization）の枠組みの一部として知られている
  • 参考文献（Katan 1986, Davey Smith and Ebrahim 2004, Didelez and Sheehan 2007, VanderWeele et al. 2014）
• Preference（嗜好）
  • 医師（介入の実施者）のある介入を他の介入（対照）よりも優先するという嗜好の指標
  • 参考文献（Korn and Baumrind 1998 , Earle et al. 2001, Brookhart and Schneeweiss 2007）
• Access（アクセス）
  • 施設までの物理的な距離や移動時間 (McClellan et al. 1994, Card 1995, Baiocchi et al. 2010)
  • 介入へのアクセスの程度が時間経過とともに変化する場合のcalendar period (Hoover et al. 1994, Dentels et al. 1998)
  • 介入や治療法の価格（リーチのしやすさ）

※4　次回のコラムにおけるmonotonicityの議論で言及するが、操作変数としてsurrogate instrumentや複数の基準・勧奨に基づく変数を用いる場合には注意が必要

 

操作変数の3条件の下での平均因果効果

操作変数の3条件を満たす変数が存在したとき興味のある平均因果効果を求めることはできるのでしょうか。結論から述べるとこの答えは部分的にNoです。あくまで操作変数の3条件が成立した際に求める（識別する）ことができるのはboundsと呼ばれる平均因果効果E[Y^a=1-Y^a=0]が含まれる幅であり、点推定を行いたい場合には次回のコラムで紹介を行う追加の仮定が成立する必要があります。次回の操作変数に関するコラムで詳細を説明します。