さて、今回ご紹介する例は、最近議論が活発な、「機械(コンピューター)が人間の作業を奪う(?)」お話です。
機械は人間から仕事(今回の例では、仕事ではなく娯楽と言ったほうが近いかもしれません)を奪ったことになるのでしょうか?それとも、真の楽しみを味わえるように、単に単純労働から開放してくれただけなのでしょうか?
昨今、人工知能がもたらす変化という文脈で行われている議論ですが、今回は、昔からある最適化アルゴリズムで、人間の仕事を奪います。皆さんでその意味を考えてみてください。
イギリスの諜報機関GCHQがクリスマスメッセージとして送った難解なパズルが公開されており、優秀な人たちを楽しませています。その第一問が、以下の「お絵かきロジック」です。日本でも一時期流行しました。イラストロジックなどとも言われ、私自身もトライした記憶があります。
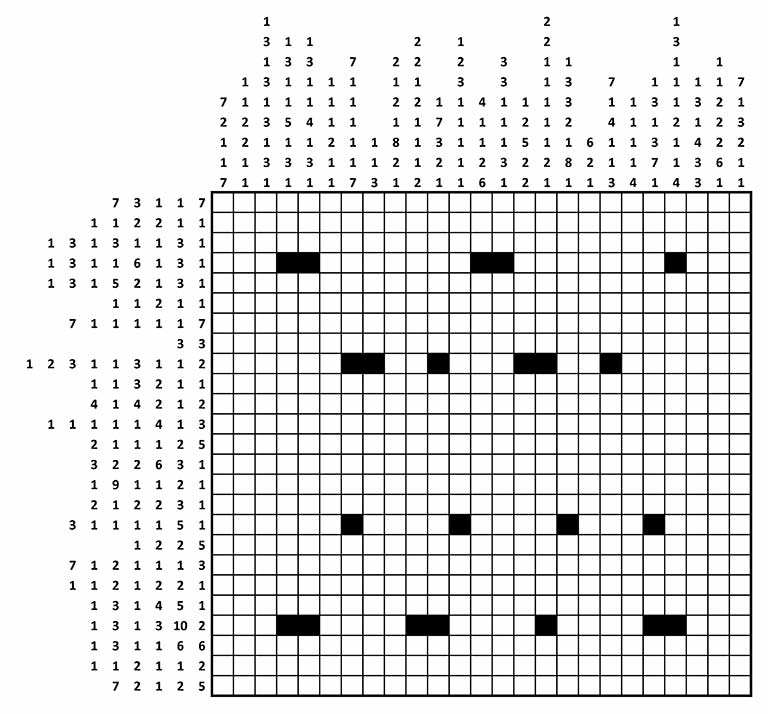
このパズルそのものについては、他の情報源に頼って欲しいのですが、簡単に説明すると、それぞれのセルを黒か白で塗りつぶすパズルで、行と列に書かれている数字は、黒マスが連続している数を順番どおりに示している「手がかり」です。いくつかのセルはすでに黒く塗りつぶされていますが、それらはこのパズルの答えを一つに確定するために必要です。
一部の箇所は、それぞれの行や列の情報だけを見て解くことが可能です。例えば、7番目の行を見てみましょう。手がかりは、(7 1 1 1 1 1 7)です。すなわち、全部で 7 + 1 + 1 + 1 + 1 + 1 + 7 = 19 個の黒いセルが必要となり、最低ひとマスは間隔が空いていないといけないので、7個の固まりの間の個数を考慮すると、7-1=6 個の白マスが必要となります。この二つの数字を足すと、19 + 6 = 25 となり一行の列数とおなじ数にちょうどなります。したがって、この結果から直ちにこの行の全てがあきらかになります。 黒7, 白1, 黒1, 白1, ・・・ ついてきていますよね。
しかし、そうは簡単にいかない箇所のほうが多いでしょう。その場合には、手がかりから部分的にしか黒く塗りつぶせないことになります。例えば、一行目を見てください。ヒントから(7 + 3 + 1 + 1 + 7) + (5 -1) = 23 個のセルを使うところまではわかります。浮いているのは、25 - 23 = 2 個です。実はこのことから、左から3列目のマスは、最初の 7 個の黒マスの一部でなければならないことが確定します。そうすると、3列目から7列目までは黒マスに塗りつぶされることが確定します。同様に、次の3つの黒マスの固まり情報から、11列目が黒セルになることが確定し、二回目の7黒マス情報から、19列目から23列目まで黒く塗りつぶせることが確定します。
このようなことを繰り返しながら、行を変え列を変えながらこのパズルを解いていくことができます。もちろん、これがこのパズルの一般的な楽しみ方です。しかし、このパズルは、実は機械に解かせることが可能です。
数理計画と最適化
混合整数線形計画法(MILP: Mixed Integer Linear Programming)という最適化の手法を使用します。今回は、2000年のRobert Boschの公式を使用します。ご興味がある方はその論文を読んでください。
今回は、その公式をつかって、SAS/ORという最適化のための機能を使用してパズルを解き、皆さんがご自身で結果を得ることを目的とします。SAS/ORを利用可能な環境にある方は、今すぐSASを起動し以下のプログラムを実行してみましょう。すぐに答えが得られてしまいます。SASをお持ちでない方、あるいはSAS/ORをお持ちでない方でも、無償で利用可能な環境を下でご紹介していますので、是非是非、答えの図をSASで描画してみてください!この答えをここに掲載することも可能なのですが、これはGCHQの一連のパズルの第一問目なので、掲載はしないでおきます。自分の手で、というより今回はできれば機械を使って、結果を手に入れてください。
SASプログラムの説明は省略します。プログラムエディタにコピペしてそのまま実行して行ってください。
まずは、手がかりとなる行と列の数字列をSASデータセット化します。
/* 手がかりとなる数字の個数の最大値をパラメータに設定 */ %let rmax = 9; %let cmax = 9; data row_data; infile datalines missover; input sr1-sr&rmax; i = _N_; datalines; 7 3 1 1 7 1 1 2 2 1 1 1 3 1 3 1 1 3 1 1 3 1 1 6 1 3 1 1 3 1 5 2 1 3 1 1 1 2 1 1 7 1 1 1 1 1 7 3 3 1 2 3 1 1 3 1 1 2 1 1 3 2 1 1 4 1 4 2 1 2 1 1 1 1 1 4 1 3 2 1 1 1 2 5 3 2 2 6 3 1 1 9 1 1 2 1 2 1 2 2 3 1 3 1 1 1 1 5 1 1 2 2 5 7 1 2 1 1 1 3 1 1 2 1 2 2 1 1 3 1 4 5 1 1 3 1 3 10 2 1 3 1 1 6 6 1 1 2 1 1 2 7 2 1 2 5 ; data column_data; infile datalines missover; input sc1-sc&cmax; j = _N_; datalines; 7 2 1 1 7 1 1 2 2 1 1 1 3 1 3 1 3 1 3 1 1 3 1 1 5 1 3 1 1 3 1 1 4 1 3 1 1 1 1 2 1 1 7 1 1 1 1 1 7 1 1 3 2 1 2 1 8 2 1 2 2 1 2 1 1 1 2 1 7 3 2 1 1 2 3 1 1 1 1 1 4 1 1 2 6 3 3 1 1 1 3 1 1 2 5 2 2 2 2 1 1 1 1 1 2 1 1 3 3 2 1 8 1 6 2 1 7 1 4 1 1 3 1 1 1 1 4 1 3 1 3 7 1 1 3 1 1 1 2 1 1 4 1 3 1 4 3 3 1 1 2 2 2 6 1 7 1 3 2 1 1 ; data hint_data; input i j; datalines; 4 4 4 5 4 13 4 14 4 22 9 7 9 8 9 11 9 15 9 16 9 19 17 7 17 12 17 17 17 21 22 4 22 5 22 10 22 11 22 16 22 21 22 22 ; run; |
次のPROC OPTMODELが心臓部分です。SAS/ORが提供している機能です。必要なパラメータや制約条件などを定義してMILPソルバを呼び出し、答えをSASデータセットに出力してくれます。
proc optmodel; /* 集合(set)とパラメータ(num)宣言 */ set ROWS; set COLUMNS; set CELLS = ROWS cross COLUMNS; num m = card(ROWS); num n = card(COLUMNS); num rmax = &rmax; num cmax = &cmax; set <num,num> HINTS; /* cluster-size sequence for row i */ num sr {i in ROWS, t in 1..rmax}; /* cluster-size sequence for column j */ num sc {j in COLUMNS, t in 1..cmax}; /* number of clusters in row i */ num kr {i in ROWS} = card({t in 1..rmax: sr[i,t] ne .}); /* number of clusters in column j */ num kc {j in COLUMNS} = card({t in 1..cmax: sc[j,t] ne .}); /* read clues from data sets */ read data row_data into ROWS=[i] {t in 1..rmax} <sr[i,t] = col(compress('sr'||put(t,best.)))>; read data column_data into COLUMNS=[j] {t in 1..cmax} <sc[j,t] = col(compress('sc'||put(t,best.)))>; read data hint_data into HINTS=[i j]; /* sanity check that sums of cluster sizes agree */ print (sum {i in ROWS, t in 1..kr[i]} sr[i,t]); print (sum {j in COLUMNS, t in 1..kc[j]} sc[j,t]); /* early and late starts for row i, cluster t */ num er {i in ROWS, t in 1..kr[i]} = if (t = 1) then 1 else (er[i,t-1] + sr[i,t-1] + 1); num lr {i in ROWS, t in 1..kr[i]} = if (t = kr[i]) then (n + 1 - sr[i,kr[i]]) else (lr[i,t+1] - sr[i,t] - 1); /* early and late starts for column j, cluster t */ num ec {j in COLUMNS, t in 1..kc[j]} = if (t = 1) then 1 else (ec[j,t-1] + sc[j,t-1] + 1); num lc {j in COLUMNS, t in 1..kc[j]} = if (t = kc[j]) then (m + 1 - sc[j,kc[j]]) else (lc[j,t+1] - sc[j,t] - 1); /* IsBlack[i,j] = 1 if cell (i,j) is black, 0 otherwise */ var IsBlack {CELLS} binary; /* IsRowClusterStart[i,t,j] = 1 if row i, cluster t starts in column j, 0 otherwise */ var IsRowClusterStart {i in ROWS, t in 1..kr[i], j in er[i,t]..lr[i,t]} binary; /* IsColumnClusterStart[j,t,i] = 1 if column j, cluster t starts in column i, 0 otherwise */ var IsColumnClusterStart {j in COLUMNS, t in 1..kc[j], i in ec[j,t]..lc[j,t]} binary; /* declare dummy objective */ min Zero = 0; /* 制約条件宣言 */ con RowSum {i in ROWS}: sum {j in COLUMNS} IsBlack[i,j] = sum {t in 1..kr[i]} sr[i,t]; con ColumnSum {j in COLUMNS}: sum {i in ROWS} IsBlack[i,j] = sum {t in 1..kc[j]} sc[j,t]; con Cluster1Row {i in ROWS, t in 1..kr[i]}: sum {j in er[i,t]..lr[i,t]} IsRowClusterStart[i,t,j] = 1; con Cluster2Row {i in ROWS, t in 1..(kr[i]-1), j in (er[i,t]+1)..lr[i,t]}: IsRowClusterStart[i,t,j] <= sum {jp in (j+sr[i,t]+1)..lr[i,t+1]} IsRowClusterStart[i,t+1,jp]; con Cluster1Column {j in COLUMNS, t in 1..kc[j]}: sum {i in ec[j,t]..lc[j,t]} IsColumnClusterStart[j,t,i] = 1; con Cluster2Column {j in COLUMNS, t in 1..(kc[j]-1), i in (ec[j,t]+1)..lc[j,t]}: IsColumnClusterStart[j,t,i] <= sum {ip in (i+sc[j,t]+1)..lc[j,t+1]} IsColumnClusterStart[j,t+1,ip]; con DoubleCoverage1 {<i,j> in CELLS}: IsBlack[i,j] <= sum {t in 1..kr[i], jp in max(er[i,t],j-sr[i,t]+1)..min(lr[i,t],j)} IsRowClusterStart[i,t,jp]; con DoubleCoverage2 {<i,j> in CELLS}: IsBlack[i,j] <= sum {t in 1..kc[j], ip in max(ec[j,t],i-sc[j,t]+1)..min(lc[j,t],i)} IsColumnClusterStart[j,t,ip]; con DoubleCoverage3 {<i,j> in CELLS, t in 1..kr[i], jp in max(er[i,t],j-sr[i,t]+1)..min(lr[i,t],j)}: IsBlack[i,j] >= IsRowClusterStart[i,t,jp]; con DoubleCoverage4 {<i,j> in CELLS, t in 1..kc[j], ip in max(ec[j,t],i-sc[j,t]+1)..min(lc[j,t],i)}: IsBlack[i,j] >= IsColumnClusterStart[j,t,ip]; /* fix variables based on slack in each row or column */ for {i in ROWS, t in 1..kr[i], j in lr[i,t]..(er[i,t]+sr[i,t]-1)} fix IsBlack[i,j] = 1; for {j in COLUMNS, t in 1..kc[j], i in lc[j,t]..(ec[j,t]+sc[j,t]-1)} fix IsBlack[i,j] = 1; /* fix variables based on hints */ for {<i,j> in HINTS} fix IsBlack[i,j] = 1; /* MILPソルバの呼び出し(自動選択) */ solve; /* 後続の処理のためのSASデータセットを作成 */ create data solution from [i j] IsBlack; quit; |
実行して、SASログに以下のように出力されていれば成功です。
NOTE: Problem generation will use 4 threads. NOTE: The problem has 2635 variables (0 free, 165 fixed). NOTE: The problem has 2635 binary and 0 integer variables. NOTE: The problem has 6933 linear constraints (2638 LE, 367 EQ, 3928 GE, 0 range). NOTE: The problem has 24252 linear constraint coefficients. NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). NOTE: The OPTMODEL presolver is disabled for linear problems. NOTE: The MILP presolver value AUTOMATIC is applied. NOTE: The MILP presolver removed all variables and constraints. NOTE: Optimal. NOTE: Objective = 339. |
最後に、PROC SGPLOT(BASE SASの機能です)を使用して答えとなる図を描画しましょう。
proc sgplot data=solution noautolegend noborder aspect=1; heatmapparm x=j y=i colorresponse=IsBlack / colormodel=(white black); xaxis display=none; yaxis display=none reverse; run; |

私は機械(SAS)のおかげで、数分でこの先のクイズに進みましたが、難しくてすぐにあきらめてしまいました。人によってはこの先の課題の方が価値がある/楽しめるため、このお絵かきロジックという単純作業から開放された喜びの方が大きいでしょう。一方、私にとっては、その先が続かなかったので結果的には唯一の楽しむ機会としてのお絵かきロジックという娯楽もSASに奪われただけという結果になってしまいました。どのような単純作業が苦痛で、どのような単純作業が娯楽なのか、皆さんはいかがお感じになったでしょうか。
無償版のSASを使って試してください!
さて、SASでは2014年から、全ての教育者、学習者、学術研究者向けに、SAS Analytics Uという取り組みのもと、無償版のSASソフトウェアの提供を開始しています。こちらでもSAS Analytics Uの解説をコンパクトにまとめているのでご活用ください。
無償版SASソフトウェアには提供形態に応じて大きくは以下の二種類があります。
- SAS University Edition
- SAS OnDemand for Academics
今回ご紹介したプログラムを動かすためには、SAS/ORというコンポーネントが必要なのですが、それにはSAS OnDemand for Academicsの方を使用する必要があります。SASを起動するまでの簡単な手順は、こちらのスライドも参考にしてください。SAS OnDemand for Academicsにログインできると、SAS Studioが起動しています。SAS Studioのプログラムエディタに、上記のプログラム3種類をそれぞれ順に貼り付けて実行していってください。
では、ハッピークリスマス!
proc iml; L = {0.03 0 0 0.1, 0.85 0.00 0.00 0.85, 0.8 0.00 0.00 0.8, 0.2 -0.08 0.15 0.22, -0.2 0.08 0.15 0.22, 0.25 -0.1 0.12 0.25, -0.2 0.1 0.12 0.2}; B = {0 0, 0 1.5, 0 1.5, 0 0.85, 0 0.85, 0 0.3, 0 0.4 }; prob = { 0.02 0.6 0.1 0.07 0.07 0.07 0.07}; L = L`; B = B`; N = 1e5; x = j(2,N); k = j(N,1); x[,1] = {0, 2}; call randseed(1); call randgen(k, "Table", prob); do i = 2 to N; x[,i] = shape(L[,k[i]], 2)*x[,i-1] + B[,k[i]]; end; y = x`; create IFS from y[c={"x" "y"}]; append from y; close IFS; idx = ceil(N*ranuni(j(500,1))); x1 = x[1,idx]`; jdx = loc(abs(x1)>0.04); idx = idx[jdx]; x1 = x[1,idx]`; y1 = x[2,idx]` - 0.1; group = ceil(5*ranuni(j(nrow(idx),1))); create Ornaments var {x1 y1 group}; append; close Ornaments; quit; data Star; x2=0; y2=10; output; run; data All; merge IFS Ornaments Star; if group=. then group=1; run; data Attrs; length Value MarkerColor $20; ID = "Ornaments"; Value = 1; MarkerColor = "Red "; output; Value = 2; MarkerColor = "Blue "; output; Value = 3; MarkerColor = "Purple "; output; Value = 4; MarkerColor = "Gold "; output; Value = 5; MarkerColor = "Chartreuse"; output; run; ods graphics / width=400px height=800px; proc sgplot data=All noautolegend dattrmap=Attrs; scatter x=x y=y / markerattrs=(size=1 color=ForestGreen); scatter x=x1 y=y1 / transparency=0.33 attrid=Ornaments markerattrs=(size=8 symbol=CircleFilled) group=group; scatter x=x2 y=y2 / markerattrs=(color=Gold size=15 symbol=StarFilled); yaxis display=none; xaxis display=none; run; |
