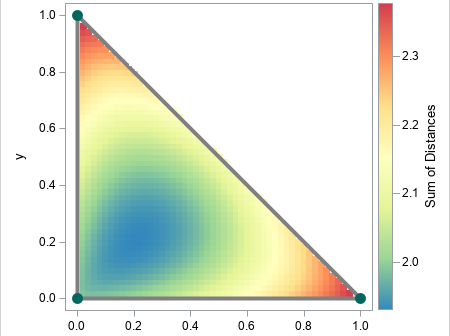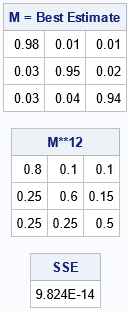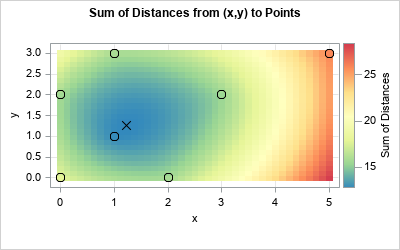
Given a set of N points in k-dimensional space, can you find the location that minimizes the sum of the distances to the points? The location that minimizes the distances is called the geometric median of the points. For univariate data, the "points" are merely a set of numbers \(\{p_1,
While writing an article about labeling a polygon by using the centroid, I almost made a false claim about the centroid. I almost claimed that that the centroid is the point in a polygon that minimizes the sum of the distances to the vertices. It is not. The point that
A colleague asked how to compute the barycentric coordinates of a point inside a triangle. Given a triangle in the plane with vertices p1, p2, and p3, every point in the triangle can be represented as a convex combination of the vertices: c1*p1 + c2*p2 + c3*p3, where c1,c2,c3 ≥
While writing an article about Toeplitz matrices, I saw an interesting fact about the eigenvalues of tridiagonal Toeplitz matrices on Nick Higham's blog. Recall that a Toeplitz matrix is a banded matrix that is constant along each diagonal. A tridiagonal Toeplitz matrix is zero except for the main diagonal, the
A Toeplitz matrix is a banded matrix. You can construct it by specifying the parameters that are constant along each diagonal, including sub- and super-diagonals. For a square N x N matrix, there is one main diagonal, N-1 sub-diagonals, and N-1 super-diagonals, for a total of 2N-1 parameters. In statistics and applied
Assigning observations into clusters can be challenging. One challenge is deciding how many clusters are in the data. Another is identifying which observations are potentially misclassified because they are on the boundary between two different clusters. Ralph Abbey's 2019 paper ("How to Evaluate Different Clustering Results") is a good way
In SAS, you can approximate the exponential of a matrix by using the EXPMATRIX function in SAS IML software. This article discusses the exponential of a matrix: what it is, how to compute it, why it is useful, and why you should think of it as a linear map that
You can use a Markov transition matrix to model the transition of an entity between a set of discrete states. A transition matrix is also called a stochastic matrix. A previous article describes how to use transition matrices for stochastic modeling. You can estimate a Markov transition matrix by using
Recently, I needed to write a program that can provide a solution to a regression-type problem, even when the data are degenerate. Mathematically, the problem is an overdetermined linear system of equations X*b = y, where X is an n x p design matrix and y is an n x 1 vector. For most
Did you know that there is a mathematical formula that simplifies finding the derivative of a determinant? You can compute the derivative of a determinant of an n x n matrix by using the sum of n other determinants. The n determinants are for matrices that are equal to the original matrix
