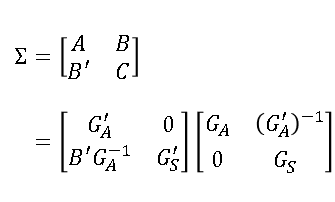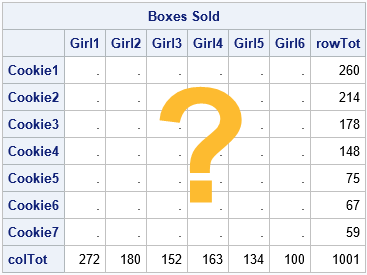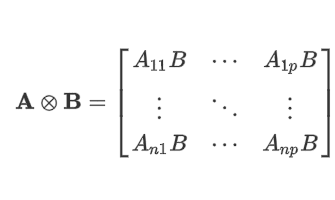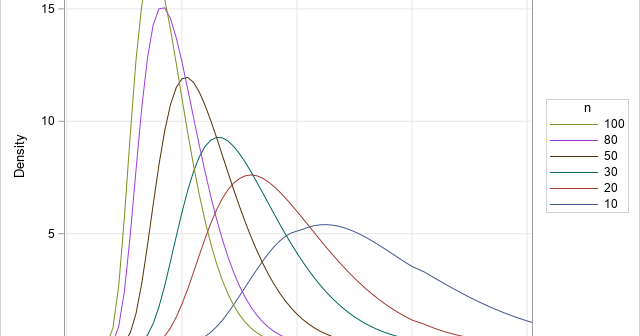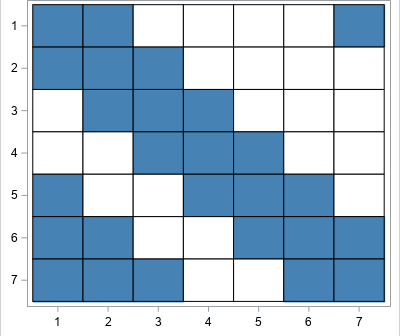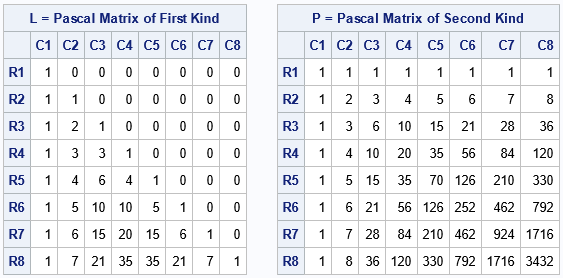
Some matrices are so special that they have names. The identity matrix is the most famous, but many are named after a researcher who studied them such as the Hadamard, Hilbert, Sylvester, Toeplitz, and Vandermonde matrices. This article is about the Pascal matrix, which is formed by using elements from