Eigenvalues of a tridiagonal Toeplitz matrix

While writing an article about Toeplitz matrices, I saw an interesting fact about the eigenvalues of tridiagonal Toeplitz matrices on Nick Higham's blog. Recall that a Toeplitz matrix is a banded matrix that is constant along each diagonal. A tridiagonal Toeplitz matrix is zero except for the main diagonal, the super-diagonal, and the sub-diagonal. Clearly, this is a very restrictive class of matrices! So restrictive, in fact, that you can write a formula that gives the N eigenvalues of an N x N tridiagonal Toeplitz matrix.

Suppose U is a square, tridiagonal, Toeplitz matrix with parameters d, a, and b, where d is the value on the diagonal, a is the value above the diagonal, and b is the value below the diagonal. Then the N eigenvalues of U are given by
$d + 2 \sqrt{ab} \cos\left( \frac{k \pi}{n+1} \right)$ for k = 1, 2, ..., N.

It is not common to be able to find an explicit formula for eigenvalues because they are the roots of a high-order polynomial. In fact, Galois theory proves that there is no general formula for high-order polynomials in terms of radicals (square roots, cube roots, etc). However, the characteristic polynomial for a tridiagonal Toeplitz matrix has so much structure that its roots can be found by using the previous formula.

This article shows two examples that illustrate the formula. The first example is a symmetric tridiagonal Toeplitz matrix. The second example is unsymmetric.

Eigenvalue of a symmetric tridiagonal Toeplitz matrix

The first example will be a symmetric tridiagonal Toeplitz matrix. For a symmetric matrix, a=b and the square root reduces to an absolute value. The following SAS IML program creates a special tridiagonal matrix (called the second-difference matrix) and computes the eigenvalues in two ways: by using the formula and by using the built-in EIGVAL function in SAS IML:

proc iml;
/* The eigenvalues of a tridiagonal Toeplitz matrix are explicit. See 
   https://nhigham.com/2022/01/10/what-is-a-tridiagonal-matrix/
*/
pi = constant('pi');
N = 5;                        /* examples are 5 x 5 (/
 
/* symmetric tridiagonal Toeplitz example */
d =  2;
b = -1;
c = j(N, 1, 0); 
c[1:2] = d // b;             /* c = {2, -1, 0, 0, 0} */
S = toeplitz(c);             /* a symmetric Toeplitz matrix */
print S;
 
/* apply the formula for exact eigenvalues */
Exact = d + 2*abs(b)*cos( pi/(N+1) * (1:N)` );
Numerical = eigval(S);
print Exact Numerical (Exact-Numerical)[L="Diff"];

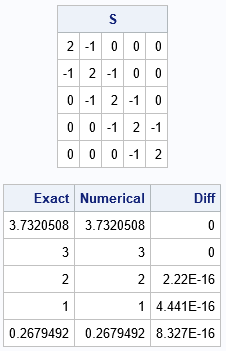
For this 5 x 5 symmetric tridiagonal Toeplitz matrix, the eigenvalues computed by the EIGVAL function are equal to their exact values to 15 decimal digits.

Eigenvalue of an unsymmetric tridiagonal Toeplitz matrix

In a previous article, I showed how to construct an unsymmetric Toeplitz matrix. The following SAS IML statements define the function and call it to create an unsymmetric tridiagonal Toeplitz matrix. Then, the eigenvalues are computed by using the EIGVAL function. Because the matrix is not symmetric, the EIGVAL function returns a two-column result, where the first column contains the real part of each eigenvalue, and the second column contains the imaginary part. For the example, the eigenvalues are real, so only the first column is needed.

/* construct a square unsymmetric Toeplitz matrix
   https://blogs.sas.com/content/iml/2023/06/12/unsymmetric-toeplitz.html
*/
start UnsymToeplitz(c, r);
   if c[1]^=r[1] then do;
      msg = "WARNING: Diagonal value is not consistent. Using " + strip(char(c[1]));
      print msg;
   end; 
   T = toeplitz(c);                   /* symmetric Toeplitz(c)  */
   TUpper = toeplitz(r);              /* symmetric Toeplitz(r)  */
   upperIdx = loc(row(T) < col(T));   /* upper triangular values */
   T[upperIdx] = TUpper[upperIdx];    /* copy upper triangular values from r */ 
   return T;
finish;
 
d = 6; a = 4; b = 1;
c = j(N, 1, 0);
c[1:2] = d // b;    /* c = {6,1,0,0,0} */
r = j(1, N, 0);
r[1:2] = d || a;    /* r = {6,4,0,0,0} */
U = UnsymToeplitz(c, r);
print U;
 
/* apply the formula for exact eigenvalues */
Exact = d + 2*sqrt(a*b)*cos( pi/(N+1) * (1:N)` );
Numerical = eigval(U)[,1];    /* real eigenvalues, so extract 1st col */
print Exact Numerical (Exact-Numerical)[L="Diff"];

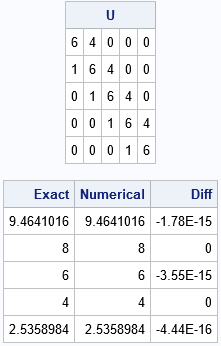
As before, the numerical eigenvalues agree with the exact value to many decimal places.

Complex eigenvalue of an unsymmetric tridiagonal Toeplitz matrix

Notice from the formula that the eigenvalues will be complex if the super-diagonal and sub-diagonal elements have different signs. In that case, the real part of each eigenvalue is d, and the imaginary part is the term that involves the square root and the cosine. For example, the following example modifies the previous matrix by setting b = -1. This produces complex eigenvalues. Because N=5 and because complex eigenvalues come in complex-conjugate pairs, one eigenvalue is real.

/* if a and b have different signs, then the eigenvalues are complex */
c[2] = -1;          /* c = {6,-1,0,0,0} */
U = UnsymToeplitz(c, r);
ExactIm = 2*sqrt(abs(a*b))*cos( pi/(N+1) * (1:N)` );    /* imaginary part */
ExactRe = d + 0*ExactIm;                                /* real part */
print ExactRe ExactIm;

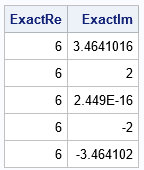
Summary

A tridiagonal Toeplitz matrix is a banded matrix with only three parameters. As such, it has a lot of structure, and you can write down an explicit formula for the eigenvalues. This article provides the formula and gives three examples. The first is a real symmetric matrix, which results in real eigenvalues. The remaining examples are unsymmetric. If the super- and sub-diagonal elements are the same sign, the eigenvalues are real. Otherwise, the eigenvalues are complex.

Blogs