A Toeplitz matrix is a banded matrix. You can construct it by specifying the parameters that are constant along each diagonal, including sub- and super-diagonals. For a square N x N matrix, there is one main diagonal, N-1 sub-diagonals, and N-1 super-diagonals, for a total of 2N-1 parameters.

In statistics and applied math, most examples of a Toeplitz matrix are symmetric. For example, the AR(1) covariance matrix is a symmetric Toeplitz matrix. A symmetric N x N Toeplitz matrix requires only N parameters. The TOEPLITZ function in SAS IML software enables you to generate a symmetric Toeplitz matrix.

Recently a SAS IML programmer asked how to construct an unsymmetric Toeplitz matrix in SAS. He mentioned that the toeplitz() function in MATLAB supports creating unsymmetric and symmetric matrices, and he wished to have something similar in SAS. This article shows how to construct a function in SAS IML that creates an unsymmetric Toeplitz matrix. An unsymmetric Toeplitz matrix is shown to the right. Note that the matrix is constant along each diagonal.

The symmetric Toeplitz matrix

Before we write a function that can create an unsymmetric Toeplitz matrix, let's recall the behavior of the built-in TOEPLITZ function in SAS IML. You specify an N-element vector, c, and the function returns a symmetric banded N x N, where c[1] is placed along the main diagonal, c[2] is placed along the first sub- and super-diagonals, c[3] is placed along the second sub- and super-diagonals, and so forth, as follows:

proc iml;
c = {10,4,3,2,1};
S = toeplitz(c);
print S;

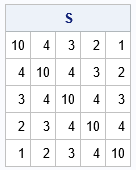
The output shows the symmetric Toeplitz matrix. Note that that the values (10,4,3,2,1) appear along the various diagonals of the matrix. The value 10 is along the main diagonal, 4 is along the first sub- and super-diagonals, and so forth.

The unsymmetric Toeplitz matrix

You can use the TOEPLITZ function to create an unsymmetric Toeplitz matrix. There are several ways to specify the syntax, but since the SAS programmer mentioned the MATLAB toeplitz() function, I will adopt the same syntax. The MATLAB function takes two N-element vectors as arguments. The first argument specifies the values for the main diagonal and the sub-diagonals. The second argument specifies the values for the main diagonal and the super-diagonals. To properly specify the matrix, the first element of each vector must be the same, but MATLAB does not enforce that requirement.

The following SAS IML function constructs two Toeplitz matrices, one from the first argument and one from the second argument. It then overwrites the super-diagonal values of the first matrix with the values from the second matrix. You can use the ROW and COL functions to locate the indices for the upper-triangular elements.

/* construct a square unsymmetric Toeplitz matrix, which is 
   constant along each diagonal band. Assume arguments c and r are the same size. */
start UnsymToeplitz(c, r);
   if c[1]^=r[1] then do;
      msg = "WARNING: Diagonal value is not consistent. Using " + strip(char(c[1]));
      print msg;
   end; 
   T = toeplitz(c);                   /* symmetric Toeplitz(c)  */
   TUpper = toeplitz(r);              /* symmetric Toeplitz(r)  */
   upperIdx = loc(row(T) < col(T));   /* indices for the upper-triangular values */
   T[upperIdx] = TUpper[upperIdx];    /* copy upper-triangular values from r */ 
   return T;
finish;
 
/* TEST */
c = {10,4,3,2,1};
r = {10,8,7,6,5};
U = UnsymToeplitz(c, r);
print U;

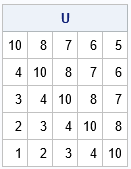
The new function returns an unsymmetric Toeplitz matrix. The values in the first argument appear on the diagonals in the lower half of the matrix. The values in the second argument appear in the upper half of the matrix.

Summary

This article discusses the symmetric and unsymmetric Toeplitz matrix. Many applications in statistics and applied math use a symmetric Toeplitz matrix, which is why the TOEPLITZ function in SAS IML returns a symmetric matrix. However, if you ever need to use an unsymmetric Toeplitz matrix, you can use the user-defined function in this article to construct it.