Platforma SAS® Viya® oferuje wiele algorytmów klasy uczenia maszynowego (machine learning, ML) czy sztucznej inteligencji (artificial intelligence, AI) do trenowania modeli predykcyjnych (klasyfikacyjnych itp.), takich jak lasy losowe (random forest) czy wzmocnienia gradientowe (gradient boosting), jak również modele uczenia głębokiego (deep learning). Choć wielokrotnie potwierdziły one swoją przydatność w praktyce, wewnętrzna architektura tych modeli i sposób odzwierciedlania modelowanych zależności są zbyt złożone, by można było w prosty sposób zinterpretować ich wskazania, na podobnej zasadzie jak ma to miejsce chociażby w przypadku modelu regresji. Charakter „czarnej skrzynki” (black box) istotnie ogranicza możliwości zastosowania tych modeli w ściśle regulowanych branżach, takich jak ubezpieczenia czy bankowość, gdzie w wielu przypadkach niezbędna jest prawidłowa interpretacja wskazań modelu (chociażby w celu upewnienia się, że model nie dokonuje prawnie niedopuszczalnej dyskryminacji).

Dlaczego należy interpretować „czarne skrzynki”

W tym kontekście kluczowego znaczenia nabiera możliwość udzielenia odpowiedzi na dwa podstawowe pytania: jak rozumieć samo pojęcie interpretowalności modelu i czy na pewno właściwie rozumiemy to, dlaczego powinniśmy zadbać o prawidłową interpretację wskazań modeli klasy AI/ML. Niniejszy artykuł stanowi pierwszy z serii dwóch artykułów poświęconych kwestii interpretowalności modeli. W części pierwszej zarysujemy problem interpretowalności modeli, zaś w części drugiej (o bardziej technicznym charakterze) omówimy w szczegółach metody interpretowalności modeli dostępne na platformie SAS® Viya®.

Zasadność tego typu rozważań starali się wykazać autorzy, pionierskiego w pewnym sensie, artykułu z 2016 roku (Marco Tulio Ribeiro, Sameer Singh, Carlos Guestrin, "Why Should I Trust You?": Explaining the Predictions of Any Classifier), którzy sformułowali – być może w nieco prowokacyjnym stylu – pytanie postawione w tytule ich pracy: dlaczego właściwie powinienem tobie ufać – gdzie zaimek „ty” wskazuje na pewien model, który w artykule pełni rolę klasyfikatora.

Autorzy zauważają m.in.: „Pomimo szerokiej akceptacji, modele uczenia maszynowego pozostają w większości czarnymi skrzynkami. Gdy tymczasem zrozumienie przesłanek kryjących się za takimi a nie innymi prognozami jest jednak bardzo ważne dla oceny tego, na ile możemy ufać naszemu modelowi. To zaufanie ma bowiem fundamentalne znaczenie, jeśli prognoza uzyskana z modelu ma służyć podejmowaniu decyzji”. (Lekarstwem, które miało przyczynić się do zwiększenia zaufania do wskazań modelu, miał stać się algorytm LIME (Local Interpretable Model-agnostic Explanations), który zaprezentujemy w drugim artykule z serii.)

Przykładowy problem

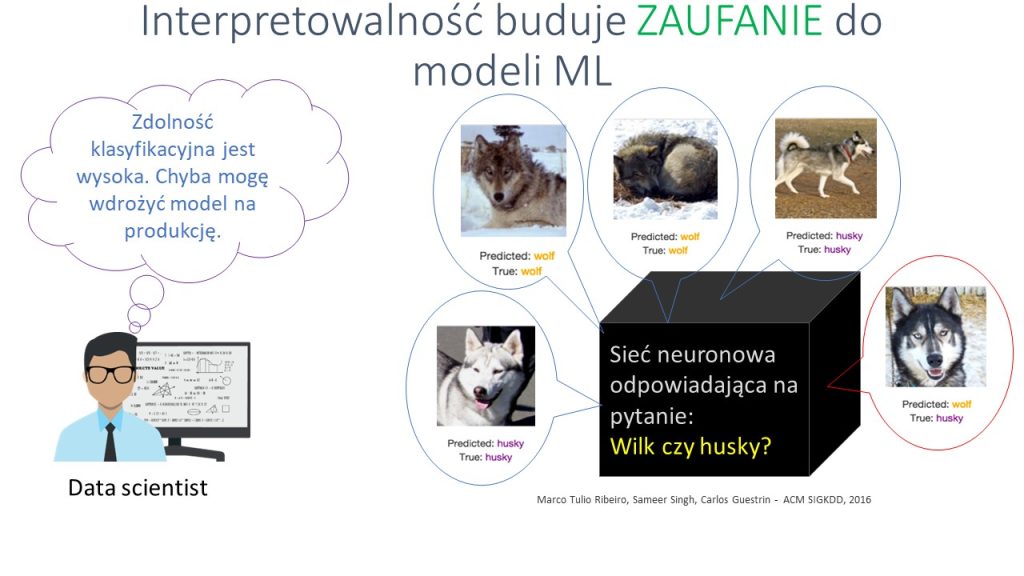
W jakim sensie interpretowalność buduje zaufanie do modeli? Posłużmy się przykładem zbliżonym do omówionego we wspomnianym artykule. Załóżmy, że jestem analitykiem danych i stworzyłem model o dość dobrych zdolnościach rozpoznawania obrazów – dobrych w rozumieniu pewnych miar jakości modelu (miar zdolności klasyfikacyjnej czy dyskryminacyjnej). Wydaje mi się więc, że jestem gotów rozpocząć wykorzystywać model w docelowym zastosowaniu. Ściśle rzecz biorąc, stworzyłem sieć neuronową, która ma za zadanie dokonywać klasyfikacji zwierząt, uwidocznionych na przedstawianych jej zdjęciach, do dwóch klas: wilka bądź – o podobnego do niego – psa husky.

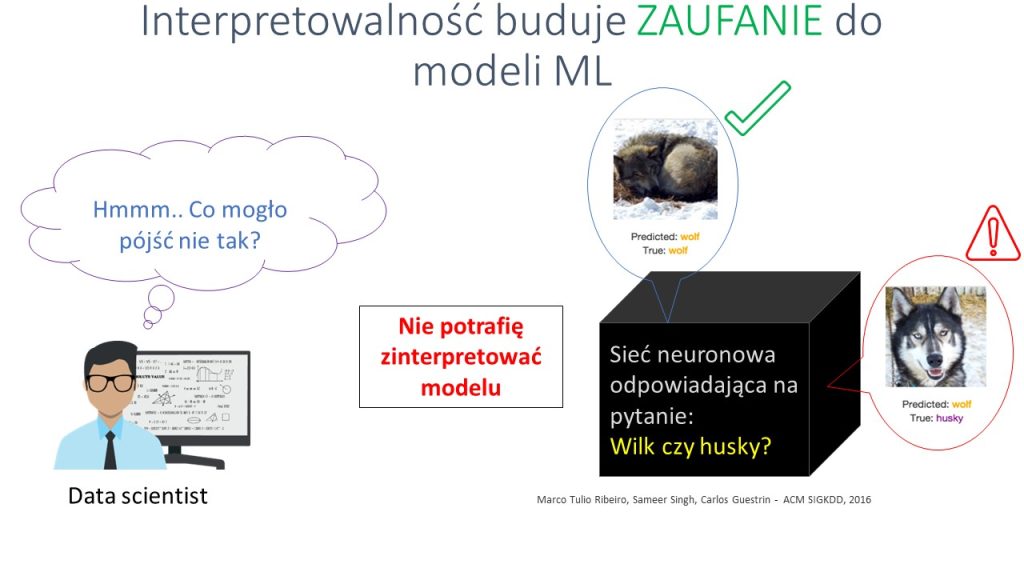
Niestety okazuje się, że model dokonuje częściowo błędnych klasyfikacji, choć przyczyny tego stanu rzeczy nie są mi znane. Nie dysponując narzędziami, które pozwoliłyby mi model zinterpretować, nie będzie mi łatwo te przyczyny znaleźć, a tym bardziej je usunąć – sieć neuronowa to model, w którym trudno powiązać wektor danych wejściowych z odpowiedzią modelu.

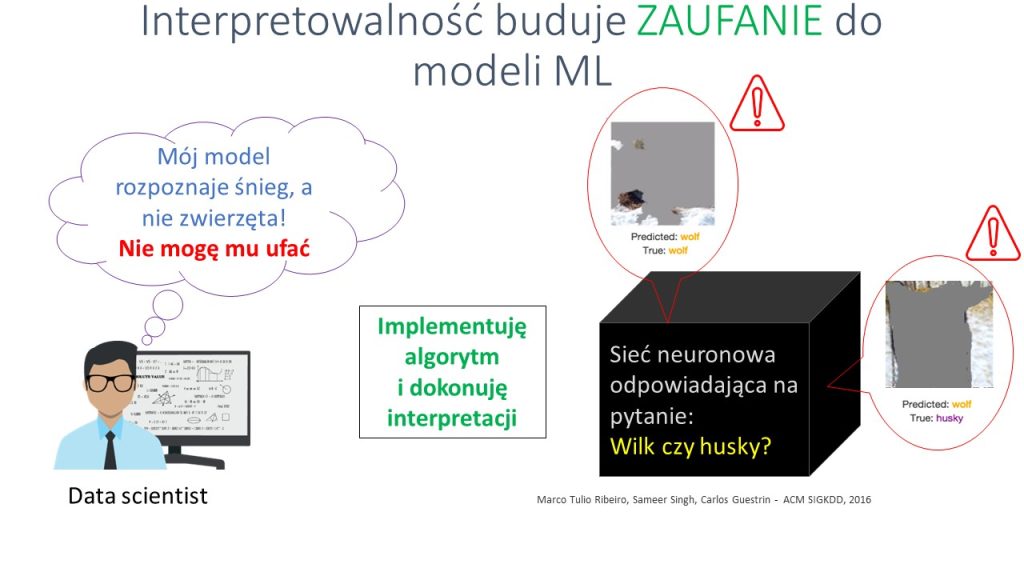
Jednakże po zaimplementowaniu algorytmu pozwalającego zinterpretować mój model dowiedziałem się, że brał on pod uwagę fragmenty zdjęcia, na których znajdował się śnieg, a nie obiekty pierwszoplanowe, czyli wizerunki zwierząt poddawanych klasyfikacji. Można by w zasadzie powiedzieć, że model był bardzo skuteczny w rozpoznawaniu śniegu, a nie wilka czy psa rasy husky. W pewnym sensie mieliśmy więc do czynienia z przypadkiem korelacji pozornej (spurious correlation) – przy czym bez możliwości sięgnięcia głębiej w strukturę modelu trudno byłoby nam ten fakt odkryć.

Jak więc możemy zadbać o to, by nasz model nie był uznany w pełni za „czarną skrzynkę”?

„Białe skrzynki”

Zacznijmy od najbardziej oczywistych przypadków, czyli modeli, które co do zasady nie wymagają pogłębionej interpretacji, bo zapewniają warunki „dobrego objaśnienia” modelu same z siebie (choć jak dotąd nie zaproponowano chyba formalnej definicji pojęcia interpretowalności modelu, opublikowano szereg artykułów poświęconych temu zagadnieniu, w tym pracę stanowiącą przekrojowe studium semantyczne, która zawiera wyliczenie cech, jakimi powinien odznaczać się dobry algorytm interpretujący model: Tim Miller, Explanation in Artificial Intelligence: Insights from the Social Sciences).

Mamy tu na myśli modele zwane niekiedy, dla kontrastu, „białymi skrzynkami” (white box), do których możemy zaliczyć regresję logistyczną czy np. niezbyt rozbudowany przypadek drzewa decyzyjnego. Modele tej klasy charakteryzują się tym, że – mówiąc umownie – ścieżka dochodzenia do odpowiedzi modelu jest na tyle prosta, że jej powiązanie ze zmiennymi wejściowymi jest niemalże bezpośrednie. W przypadku regresji liniowej mamy prostą postać funkcyjną oraz wagi (współczynniki modelu), które są wprost powiązane z wartością prognozowanej zmiennej celu (zmiennej objaśnianej). Interpretacja takiej wagi odbywa się jednak z reguły na zasadzie ceteris paribus, czyli przy założeniu, że wartości pozostałych zmiennych pozostają niezmienione.

Z kolei samą istotność danej zmiennej możemy ocenić (w klasycznym modelu regresji liniowej, gdzie zakładamy, iż składnik losowy ma rozkład normalny i jest IID, a więc np. nie występuje autokorelacja czy heteroskedastyczność) przy pomocy statystyki t o rozkładzie Studenta. Model w postaci drzewa można uznać za nieco bardziej skomplikowany, ponieważ przez drzewo decyzyjne rozumiemy – w dużym uproszczeniu – listę cech, wartości progowych oraz przepis na rozrost drzewa (np. metoda CART), a ogólną istotność zmiennej możemy analizować np. poprzez monitoring spadku wartości indeksu Giniego dla każdej zmiennej użytej do budowy drzewa. Jednak dopóki drzewo nie jest nadmiernie rozbudowane, nadal jesteśmy w stanie stosunkowo łatwo je zinterpretować.

Interpretowalność ex ante

Sytuacja komplikuje się jednak wtedy, kiedy chcemy wykorzystać bardziej zaawansowane modele klasy AI/ML, takie jak sieci neuronowe, wspomniane lasy losowe czy wzmocnienia gradientowe. „Droga” jaką pokonuje obserwacja od wejścia do modelu sieci poprzez wszystkie możliwe warstwy ukryte zbudowane z potencjalnie bardzo dużej liczby neuronów, z uwzględnieniem takich cech, jak wagi czy funkcje aktywacji, jest na tyle skomplikowana, że nie daje się wytłumaczyć w postaci prostych zależności. Sieć neuronowa to typowy przypadek „czarnej skrzynki”, czyli modelu, w którym jesteśmy w stanie wyestymować (czy skalibrować) poszczególne komponenty modelu (takie jak wagi), jednak nie rozumiemy wewnętrznych mechanizmów, które prowadzą do określonej odpowiedzi modelu. Nie jesteśmy w stanie w prosty sposób stwierdzić, dlaczego model dał taką a nie inną odpowiedź na konkretny sygnał wejściowy. W szczególności przypisanie istotności poszczególnym zmiennym wejściowym w ogólnym przypadku nie jest możliwe bez dodatkowych zabiegów.

O jakich zabiegach mowa, tzn. jakie podejścia możemy zastosować, aby być w stanie objaśnić działanie „czarnej skrzynki”? Możemy zdecydować się np. na zastosowanie metod zastępczych (proxy), czyli metod, których myślą przewodnią jest doprowadzenie do zastąpienia właściwego modelu AI/ML innym modelem, który byłby łatwiejszy w interpretacji. Nie są to więc metody interpretacji modeli w ścisłym rozumieniu tego pojęcia (co sugeruje samo użycie słowa proxy). Do metod tej klasy zaliczamy m.in.:

• Metodę modelu zastępczego (surrogate model approach) – w pierwszym rzędzie trenujemy czarną skrzynkę na zbiorze uczącym, a następnie podstawiamy wyjście z tego modelu w charakterze zmiennej celu w modelu, który czarną skrzynką nie jest.
• Druga metoda to specyficzny przypadek podejścia champion-challenger, w którym czarna skrzynka służy za benchmark dla modelu, który czarną skrzynką nie jest. W tym podejściu wykorzystujemy model klasy AI/ML na potrzeby „ustawienia odpowiednio wysoko poprzeczki” dla możliwych do uzyskania w danych warunkach (np. na konkretnym zbiorze testowym) miar jakości modelu, które służą za punkt odniesienia dla modeli typu „biała skrzynka”. Domyślnie są one challengerami, które mają dorównać championowi w postaci modelu AI/ML.
• Wreszcie podejście trzecie, które zakłada, że modele klasy AI/ML wykorzystujemy jedynie do wstępnej selekcji zmiennych, by następnie te właśnie zmienne wykorzystać w modelach poddających się bezpośredniej interpretacji („białych skrzynkach”).

Wszystkie trzy omówione podejścia można łatwo zrealizować na platformie SAS® Viya®, która natywnie wspiera m.in. podejście champion-challenger, umożliwiając budowę konkurujących modeli i wybór najlepszego według zadanych kryteriów.

Interpretowalność ex post

Najczęściej nie chodzi nam jednak o to, by budować pełne modele proxy dla modelu klasy AI/ML, ponieważ wiąże się to z dodatkowymi kosztami i potencjalną utratą zalet modeli tej klasy. Jeżeli zależy nam na wszystkich zaletach złożonych modeli klasy AI/ML, pozostaje nam wykorzystanie dedykowanych algorytmów służących interpretacji odpowiedzi modelu, który już zbudowaliśmy i uznaliśmy wstępnie za „optymalny” (w rozumieniu zadanych kryteriów oceny jakości modelu). Na platformie SAS® Viya® zaimplementowano natywnie kilka metod służących diagnostyce ex post (a więc bez stosowania metod zastępczych, bezpośrednio na docelowym modelu „czarnej skrzynki”):

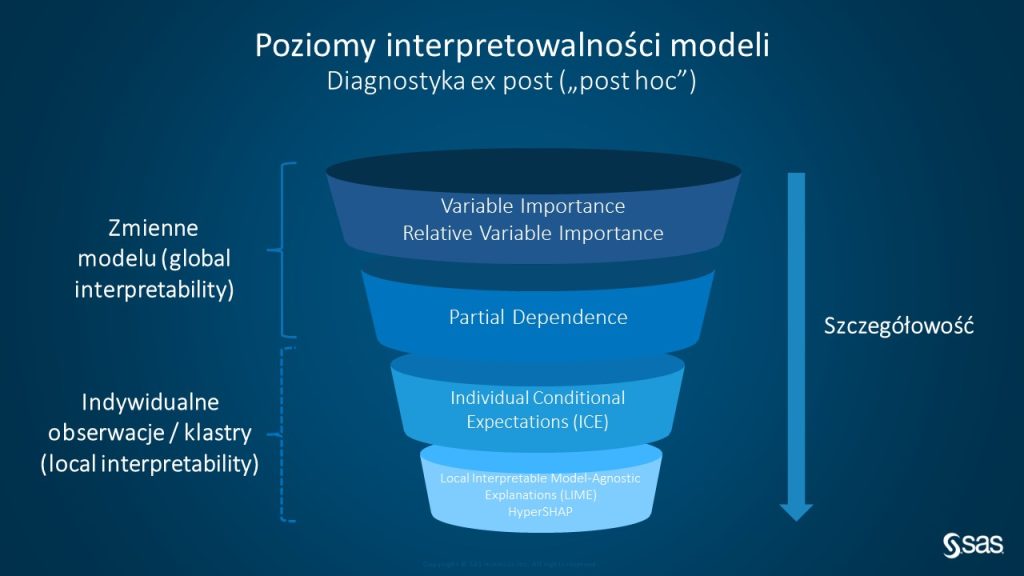
• Variable Importance (VI) oraz Relative Variable Importance, które przede wszystkim pozwalają nam uszeregować zmienne pod względem istotności.
• Partial Dependence (PD) oraz Individual Conditional Expectation (ICE), które, podobnie, pomagają nam odpowiedzieć na pytanie o to, z jaką siłą (w jaki sposób) konkretne zmienne wpływają na odpowiedź modelu.
• A także wspomniany już wcześniej algorytm LIME czy HyperSHAP, które przede wszystkim pomagają nam wyjaśnić odpowiedź modelu dla konkretnych obserwacji.

Wymienione algorytmy możemy podzielić na dwie grupy pod względem tego, czy dany algorytm pozwala nam na ogólną interpretację działania modelu jako całości, czy też raczej pozwala przyjrzeć się bliżej wyłącznie odpowiedzi modelu dla konkretnego sygnału podanego na wejściu. Według tego kryterium dzielimy algorytmy na interpretujące model globalnie lub lokalnie.

Globalna interpretacja modelu jest pewnym ideałem, do którego dążymy, ale nie zawsze łatwo osiągalnym. Dlatego w praktyce duże znaczenie mają algorytmy pozwalające objaśnić model lokalnie. Na poziomie pojedynczej obserwacji, zależność pomiędzy wejściem a wyjściem może być znacznie prostsza w opisie. Np. może zależeć liniowo od pewnego zestawu cech, a nie – jak ogólnie w modelu – kształtować się wg znacznie bardziej skomplikowanego przepisu.

Szczegóły wymienionych wyżej metod przedstawimy w kolejnym artykule z serii.