I ran across an interesting conundrum the other day. The intent was to compare the value of X to a list of desired values, and if X matched one of the values in the list, set Flag to 1, otherwise set Flag to 0.  I wrote and executed this test program, then reviewed the results. Oddly, only observations 1 and 9 had Flag set to 1. However, I could clearly see that the values of X in observations 3,5,and 7 should also have had Flag set to 1, because those values of X were definitely on my list!

data test;
   do id=-0.2 to 0.2 by .05;
      x=id;
      if x in (-0.2 -0.1 0 0.1 0.2) then flag=1;
      else flag=0;
      output;
   end;
run;
proc print data=test;
run;

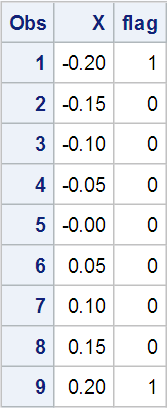
What dark force could be thwarting my fairly straightforward computation? Master Yoda once said "In a dark place we find ourselves, and a little more knowledge lights our way." So off to the SAS Online Docs I went to find enlightenment. In the end, it was just that age-old computer problem of representing base ten numeric values exactly when working with double-precision (8 byte) floating point numbers. Most computer systems use floating point numeric representation because numbers of widely varying magnitude can be represented - numbers from ≈ 1.7976931348623157x10³⁰⁸ to ≈ 2.2250738585072014x10⁻³⁰⁸. But computers actually store and process binary or hexadecimal values, not base ten. And the scheme for representing floating point numbers with only 8 bytes means that many base ten numbers can't be represented exactly in binary or hex. So a floating point number is actually a signed approximation of the value specified which can store large magnitude numbers with limited precision. There's a lot of great background information in the online docs Numerical Accuracy in SAS Software article. The section on Numeric Comparison Considerations gets right to the heart of our problem. The docs suggest using rounding during comparison, and a quick test of that technique produced the correct results:

data test2;
   do X=-0.2 to 0.2 by .05;
      if round(x,0.01) in (-0.20 -0.10 0.00 0.10 0.20) then flag=1;
      else Flag=0;
      output;
   end;
run;
proc print data=test2;
run;

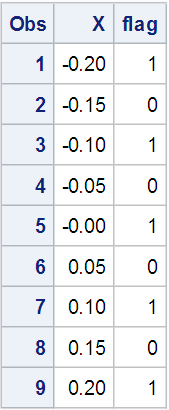
But wouldn't it be awesome if we could process exactly the value specified in our programs? Most databases support storing numeric values as exact, fixed-decimal instead of floating point without limiting size to 8 bytes in a data type named DECIMAL. In Chapter 3 of my book "Mastering the SAS^® DS2 Procedure”, we discuss the fact that, while you can't store DECIMAL data in a SAS data set, you can process DECIMAL data in base SAS using DS2. Of course, because DECIMAL values store exact numbers and allows a maximum of 52 digits of precision, eventually we'll hit a magnitude limit. But in this case, 52 digits of precision is more than sufficient to meet our needs our needs. So this DS2 program provides yet another solution to our dilemma, and one that does not require rounding:

proc ds2;
data test3/overwrite=yes;
   dcl decimal (5,2) X;
   dcl int Flag;
   method run();
   	do X=-0.2 to 0.2 by .05;
   	   if x in (-0.20 -0.10 0.00 0.10 0.20) then flag=1;
         else Flag=0;
   	   output;
   	end;
	end;
enddata;
run;
quit;
proc print data=test3;
run;

So there you have it, the DOUBLE vs. DECIMAL dilemma deciphered. You can download the code from this post here.
Until the next time, may the SAS be with you!
Mark