“Los seguros no se piensan… se toman, porque los siniestros no se planean... llegan”

Hoy nos sumergiremos en la actividad aseguradora, pero no sin antes mencionar que en el mundo de los sommelier se comenta, con humor, que los seguros son como el vino… si usted no nota la diferencia ¡¡Elija el más barato!! (pero no se queje del dolor de cabeza al día siguiente…).

Volviendo al tema de este artículo, todos sabemos que el entorno que nos rodea está lleno de situaciones que pueden depararnos algún que otro susto y más de un quebranto económico. Nada ni nadie está libre de sufrir un accidente, un impago, un robo, etc. Al margen de los aspectos humanos o emotivos, la ocurrencia de estos sucesos puede provocar pérdidas que pueden hacernos la vida más difícil. La existencia y contratación de seguros permite aliviar el impacto material de estas contingencias.

De hecho, es comúnmente reconocido que el negocio asegurador contribuye al crecimiento económico y a la prosperidad de muy diversas formas. Desde un punto de vista macroeconómico, permite un mayor grado de eficiencia facilitando la transferencia de riesgos de unos agentes a otros. Por otro lado, desde el punto de vista microeconómico, ayuda a que los individuos minimicen el impacto de acontecimientos ni esperados ni deseados, lo cual les permite organizar sus asuntos con mayores dosis de certidumbre.

La actividad aseguradora consiste entonces en ponerle precio a un riesgo: el riesgo de que se incendie tu casa, o de que tengas un siniestro con tu automóvil, etc.

El riesgo, en sí, no es malo. De hecho, como mencionamos anteriormente, aceptar los riesgos a los que otros están expuestos es el oficio de las aseguradoras, empresas consideradas entre las más sólidas y longevas del tejido empresarial de cualquier país desarrollado.

En la actividad aseguradora el precio a definir será equivalente a la suma de los costos más los beneficios, en donde el desafío central es establecer el costo de futuros reclamos para cada asegurado, constituyendo esto un compromiso para la compañía aseguradora puesto que es el dinero que algún día la aseguradora deberá pagarle al cliente.

Estos compromisos tienen un elevado grado de incertidumbre tanto en su cuantía como en el instante de tiempo en que se producirán. Esto origina que, para establecer el valor esperado de la pérdidas siniestrales, las compañías aseguradoras deben estimar con qué frecuencia ocurrirán los reclamos y cuánto costará cada reclamo. Ajustar por separado la frecuencia y la severidad de los siniestros puede proporcionar una mejor comprensión de la forma en que los factores pueden afectar la cuantía total de siniestros. Matemáticamente, suele expresarse, como la multiplicación entre (donde el valor esperado se simboliza como E):

                                       E[Pérdida] = E [Número de reclamos] x E [Costo por reclamo]

Es decir,

                                       E[Pérdida] = E [Frecuencia] x E[Severidad]

La idoneidad del asegurador debe basarse en ser capaz de sentirse satisfecho en que puede establecer tarifas adecuadas en relación con el riesgo asumido.

Un enfoque para predecir el comportamiento de la frecuencia es utilizar las técnicas de modelización denominadas GLM (Modelos Lineales Generalizados).

Modelos Lineales Generalizados (GLM)

Los modelos lineales generalizados nacieron como algoritmos que permiten la estimación de una serie de distintos modelos de regresión estadística dentro de un mismo marco teórico. El uso de GLM ha demostrado ser de un valor sustancial gracias a la amplitud de modelos que contiene, y por la cantidad de medidas de bondad de ajuste posibles de usar.

Al igual que en los modelos tradicionales, los modelos lineales generalizados son utilizados para valorar y explicar la relación entre una variable respuesta y variables explicativas, cuyo objetivo a contemplar será conseguir aquel modelo que sea capaz de predecir la experiencia futura sin ajustarse en exceso a determinados momentos pasados que resulten o puedan ser atípicos.

En el contexto del mercado asegurador, estos modelos son importantes para explicar la frecuencia o magnitud de los siniestros de las distintas coberturas, tomando datos del asegurado como variables predictivas. El efecto de las variables predictivas será estimado con información histórica de las bases de datos de la compañía y la mano experta de quien, conociendo el negocio, puede evitar interpretaciones erróneas.

Una de las grandes ventajas de usar modelos GLM es la posibilidad de usar la función de enlace, que nos permite acotar resultados. Por ejemplo, en el caso de predicción de variables de conteo, donde carece de sentido la existencia de números negativos, con el uso de una función logarítmica solucionamos el problema.

Por otro lado, usar modelos lineales generalizados permite trabajar con variables respuestas que no se distribuyen normalmente en torno a su media.

Podemos mencionar que el modelo de Poisson, perteneciente a los modelos lineales generalizados, es el más habitualmente utilizado como punto de partida en los modelos de frecuencia. Otra de las distribuciones de probabilidad que se usan para modelar la frecuencia es la Binomial Negativa. Ahora bien, cuando los datos observados muestran una proporción de valores ceros mayor de la que puede ser explicada por un modelo estándar como ser el de Poisson y Binomial Negativa, existe una vía para resolver el problema que es el denominado “Zero Inflated Model”. Este tipo de modelo además de solventar el problema de exceso de ceros también permite solventar el problema de la sobre dispersión (ocurre cuando la varianza empírica es mayor que la varianza teórica para una distribución en particular).

PROC GENMOD

SAS cuenta con un procedimiento denominado “PROC GENMOD” que permite ajustar a modelos lineales generalizados con varias funciones de enlace incorporadas y distribuciones de probabilidad. Algunas de las funciones de enlace disponibles son identity, log, logit, probit, power, cumulative complementary log-log, cumulative logit, cumulative probit y complementary log-log. Proc Genmod también permite funciones de enlace definidas por el usuario.

Las distribuciones de probabilidad disponibles son Binomial, Gamma, Gaussiana Inversa, Geométrica, Multinomial, Binomial Negativa, Normal, Poisson, Zero-Inflated Poisson y Zero-Inflated Binomial Negativo. Información sobre modelos lineales generalizados aquí.

Un ejemplo del PROC GENMOD se encuentra en el siguiente link.

También se puede utilizar el PROC COUNTREG, que analiza los modelos de regresión en los que la variable dependiente toma valores enteros o de conteo no negativos. La variable dependiente suele ser un recuento de eventos, que se refiere a la cantidad de veces que ocurre un evento.

PROC SEVERITY

 

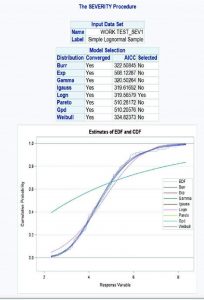
Por otra parte, el modelo habitual para modelar la severidad es el Gamma. En SAS, el procedimiento PROC SEVERITY permite estimar los parámetros de cualquier distribución de probabilidad continua arbitraria que se utiliza para modelar, entre otros, la magnitud de los montos de primas pagados por una compañía de seguros, es decir la severidad o intensidad del costo medio.

PROC SEVERITY proporciona un conjunto predeterminado de modelos de distribución de probabilidad que incluye las distribuciones Burr, Exponencial, Gamma, Pareto Generalizado, Gaussiano Inverso (Wald), Lognormal, Pareto, Tweedie y Weibull. Este procedimiento de SAS permite calcular las estimaciones de los parámetros del modelo, sus errores estándar y su estructura de covarianza utilizando la metodología de máxima verosimilitud, además de elegir la mejor distribución de acuerdo con un criterio de selección que se especifique.

Adicionalmente, permite utilizar siete estadísticos diferentes de ajuste como criterios de selección como ser: la log likelihood, el criterio de información Akaike (AIC), el criterio de información Akaike corregido (AICC), el criterio de información bayesiano de Schwarz (BIC), el criterio de Kolmogórov-Smirnov (KS), el estadístico de Anderson-Darling (AD) y el estadístico de Cramér von Mises (CvM). Cabe aclarar, que toda modelización debe tener en cuenta el principio de parsimonia, es decir, obtener el mejor modelo con el menor número de parámetros.

Un ejemplo del procedimiento “PROC SEVERITY” es posible encontrarlo en este link.

 

PROC HPCDM

Aunque los modelos de distribución de pérdidas para frecuencia y severidad son útiles por sí solos, como acabamos de mencionar, a menudo son un medio para el objetivo final: estimar las medidas de riesgo que requiere el cálculo de la probabilidad de distribución de la pérdida agregada/total en la que una empresa aseguradora espera incurrir en un período de tiempo determinado.

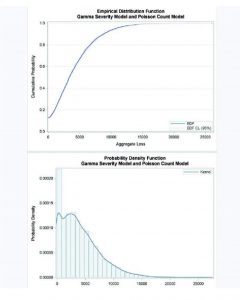
Recuérdese, que una compañía de seguros por la naturaleza misma de su negocio necesita lidiar con las pérdidas sufridas por sus asegurados. Es importante no sólo identificar los factores que causan las pérdidas sino también cuantificar lo esperado en pérdidas para gestionar mejor el riesgo y estimar los requisitos de capital basados ​​en el riesgo que se exigen por las regulaciones.

Por consiguiente, un objetivo central de toda compañía aseguradora será entonces estimar no solo la pérdida promedio sino también la peor pérdida que espera observar en un período de tiempo particular. Alguna de las medidas de riesgo se define en términos de un percentil de la distribución de pérdidas agregadas (VaR) o la media de un extremo región de la cola de la distribución de pérdidas (TVaR).

SAS cuenta con un procedimiento denominado PROC HPCDM, que toma como entrada los modelos de frecuencia y severidad estimados, simulando una muestra de pérdida agregada de acuerdo con un tamaño que se especifique, permitiendo obtener un conjunto de datos de salida (estadísticos como media, desvío, etc. y percentiles) que permita obtener una medida de riesgo a elección. Estas estadísticas resumidas y estimaciones de percentiles proporcionan medidas cuantitativas muy valiosas para evaluar el riesgo. Un ejemplo de estas medidas puede ser el valor a riesgo obtenido en el percentil 99.5.

Un ejemplo del PROC HPCDM puede ser visualizado aquí.

PROC COPULA

Por último, como un plus de este blog, es importante mencionar el concepto de cópulas, en donde la teoría de cópulas encuentra múltiples aplicaciones en el campo actuarial. La dependencia entre riesgos es allí objeto de una atención creciente. Por esta razón, donde exista una diversidad de riesgos que puedan presentar dependencia entre sí, habrá campo para intentar la aplicación de las cópulas. Las normativas de las entidades aseguradoras tienden a incluir en los sistemas de solvencia una pluralidad de riesgos que les afectan.

De estos riesgos no interesa sólo cómo se distribuyen aislada o separadamente (distribución marginal) sino también de qué manera dependen los unos de los otros. Puede ocurrir que en condiciones normales no exista dependencia entre ellos, pero cuando haya crisis las cosas empeoren en todos ellos. Ésta es una situación en que el coeficiente de correlación no es instrumento adecuado, mientras que la aplicación de la teoría de cópulas puede ofrecer respuesta satisfactoria.

El planteamiento intuitivo de este concepto consistiría en decir que las cópulas son funciones de distribución de varias variables que contienen la norma reguladora de la dependencia entre dichas variables. Es decir, que en la cópula reside la forma en que dependen unas variables de otras. Si cambiamos la cópula, alteraremos la dependencia de estas variables entre sí; ello nos sugiere que la utilidad de estas funciones está en servir de modelos de la dependencia entre variables aleatorias, entre riesgos que afecten a cierta actividad.

En otras palabras, las cópulas son expresiones matemáticas de la dependencia entre dos o más variables aleatorias y contienen toda la información relativa a la dependencia entre esas variables.

Los diferentes tipos de cópulas se centran en diferentes medidas de dependencia, incluyendo correlación lineal, correlación de rango y dependencia de cola. Para aplicaciones financieras, la dependencia de la cola es de especial importancia, porque mide la dependencia cuando todas las variables aleatorias tienen valores extremos. En los seguros distintos al de vida, es clara la posible aplicación de las cópulas; pensemos, por ejemplo, en contratos que cubran riesgos dependientes entre sí, o en la posibilidad de acontecimientos que afecten simultáneamente a varias pólizas.

SAS cuenta con un procedimiento denominado “PROC COPULA”, que permite aplicar el enfoque de cópulas. De las cópulas que PROC COPULA admite, la cópula t captura la dependencia tanto en la cola izquierda (inferior) como en la derecha (superior) cola, la cópula Gumbel captura la dependencia en la cola derecha, y la cópula Clayton captura la dependencia en la izquierda. Información sobre este procedimiento, se puede encontrar en https://support.sas.com/documentation/onlinedoc/ets/132/copula.pdf.

Si tenés dudas, consulta o querés conocer más información, te invitamos a unirte a nuestra comunidad de actuarios en Slack! 

¡Los espero en la próxima entrega! ¡Muy feliz año nuevo!