注) 本コラムは『経時的に変化する治療(Time-varying treatments)に対する因果推論』と題した以前のコラムを、時間依存性治療に関する部分と周辺構造モデルにおけるIPTW法に関する部分に分割し、内容の追加と修正を行い再構成したものの一部となります。
はじめに
以前のコラムでは、「時間依存性治療とはなにか」、「時間依存性治療の因果効果はどのように定義されるのか」、「定義した因果効果はどう推定すれば良いか」について紹介しました。時間依存性治療の因果効果の推定にあたっては、一般に条件付けに基づく手法(e.g., 回帰、層別化、マッチング)は不適であり、g-methods※1と総称される推定手法が広く用いられています。本コラムでは、それらの中でも直感的な理解や実装が最も容易である「周辺構造モデルにおけるIPTW法(inverse probability of treatment weighting (IPTW) of marginal structural models (MSMs)」の理論とSASでの実装方法について簡単に紹介します。コラム全体の流れは以下の通りです。
- 時間固定性治療(time-fixed treatments)※2に対する周辺構造モデルとIPTW法の紹介
- IPTW法の概要
- 周辺構造モデルの設定がなぜ必要か
- 時間依存性治療(time-varying treatments)に対する周辺構造モデルとIPTW法の紹介
- SASでの実装
- まとめ
なお、本コラムは統計的因果推論に関する基本的な理解があることを前提としております。また、文献や書籍によっては、IPTW(Inverse probability of treatment weighting)は、単にIPW(Inverse probability weighting)と記載される場合もあります。しかし、IPW(逆確率重み付け)は治療効果の直接的な推定を目的とした治療変数に関する重み付け以外にも、打ち切りに対する補正(i.e., 打ち切り変数に関する重み付け)等でも用いられることがあり、本コラムでは前者であることを強調するためにIPTWと記載します。加えて、本コラムでは連続もしくは二値であるアウトカム(結果変数)が、研究最終測定時点でのみ測定される状況を想定します。アウトカムが生存時間(time-to-event)である場合や各時点の治療実施後に繰り返し測定される場合など※3、異なる状況における議論についてはreferenceにある文献等をご参照いただくか、著者宛に別途ご連絡いただけると幸いです。
※1 (i) Inverse probability of treatment weighting of marginal structural models(周辺構造モデルにおけるIPTW法)、(ii) g-computation algorithm formula("g-formula")、(iii) g-estimation of stractural nested model(構造ネストモデルにおけるg-estimation)のという3手法の総称
※2 執筆時点で対応する定訳が存在しないという筆者の認識であるが、本コラムにおいては時間固定性治療という訳をあてる
※3 打ち切りや脱落、変数の測定誤差など、交絡以外のバイアスの原因となる要素は本コラムにおいて存在しないものとしている
時間固定性治療に対する周辺構造モデルとIPTW法
・IPTW法の概要
本セクションでは、ベースライン時点で行われる二値治療の平均因果効果を推定対象とし、IPTW法と周辺構造モデルについて紹介します。ただし、以前のコラムで紹介したように、ある単一時点(ベースライン)で行われる治療は、因果関係を議論していく上では時間固定性治療の一種として分類されます。よって、本セクションの内容は時間固定である治療全体に適用可能であることにご注意ください。
さて、はじめに記法を以下のように置きます。
- n:サンプルサイズ
- A:治療(1:treat, 0:untreated)
- L:共変量ベクトル
- Y:アウトカム(連続 or 二値)
- Ya=1, Ya=0:潜在アウトカム
そして、我々が興味がある効果は「集団全員に対してある治療Aを行った場合には、治療を行わなかった場合と比較してどの程度平均的に効果があったか」、すなわち、差分のスケールでの平均因果効果E[Ya=1]-E[Ya=0]であるとします。
次に、上記の平均因果効果の推定(識別)のためにいくつかの仮定(identifiable conditions)を置きます。各仮定が意図することについては別コラムで紹介していますので、適宜リンク先もご参照ください。なお、現実的にはこれらの仮定の成立を認めることが妥当であるかの議論が必要ですが、本コラムではすべて成立するものとします。
- 一致性(consistency):If Ai = a, then Yia = Yi for all a
- 条件付き交換可能性(conditional exchangeability):Ya⫫A|L for all a
- 正値性(positivity):If f[L=l]≠0, 0 < f[Ai=a|L=l] < 1, for all l, i, a
ここで、潜在アウトカムの期待値E[Ya]は、仮定の下で下式のように展開することが可能です。式中のは個人に与えられる重みであり、Iは()内の条件に合致する場合には1を、そうでない場合には0をとる指示関数(indicator function)です。
\(
E[Y^{a}]=E[Y|A=a, L]=\frac{1}{n}\sum_{i=1}^{n}YI(A=a)\frac{1}{f(A|L)}\\
\)
すなわち、
\(
E[Y^{a=1}]=E[Y|A=1, L]=\frac{1}{n}\sum_{i=1}^{n}YI(A=1)\frac{1}{Pr(A=1|L)}\\
E[Y^{a=0}]=E[Y|A=0, L]=\frac{1}{n}\sum_{i=1}^{n}YI(A=0)\frac{1}{Pr(A=0|L)}=\frac{1}{n}\sum_{i=1}^{n}YI(A=1)\frac{1}{1-Pr(A=1|L)}\\
\)
つまり、識別可能条件の下では、関心のある因果効果を定義する潜在アウトカムの期待値E[Ya=1]、E[Ya=0]は「実際に治療を受けた(受けなかった)人の観測されたアウトカムの値」と「共変量で条件付けた場合に実際に受けた治療を受ける確率の逆数(重み)」の積を平均した値(重み付け平均)となります。これは言い換えると、治療を受けた場合、受けなかった場合の潜在アウトカムの期待値であるE[Ya=1]、およびE[Ya=0]は、それぞれ治療群(A=1)と対照群(A=0)の情報のみを用いて表現されることを意味しており、後ほど登場する周辺構造モデルとも関連しているポイントの1つです。
上記の内容は数式展開のみから言及できることでしたが、因果効果に興味のあるケースのほとんどで我々が行いたいことは、得られたデータを用いて平均因果効果を推定することです。そこで、推定という観点で改めて上式を見てみると、前者のアウトカムの値はデータとして群ごとに得ることが可能です。一方で、個人に与えられる重みの分母にあたり、傾向スコア(propensity score)※4と呼ばれる共変量Lでの条件付きの治療確率Pr[A=1|L]の値については問題が発生することがあります。Pr[A=1|L]は、共変量Lで集団を層別化することが可能であるならば、各層内のAに関する単純な算術平均を用いて特定のモデルを置くことなく(ノンパラメトリックに)推定することが可能です。また、ランダム化が行われる実験では、その値は群割付の確率に相当します(e.g., 割付比が1:1である単純ランダム化実験では0.5)。しかし一般に、共変量ベクトルLは高次元かつ連続変数を含むことから層に分けることは現実的ではなく、特定のモデル(e.g., ロジスティック回帰モデル)を用いてPr[A=1|L]を推定(近似)することとなります。つまり、モデルの誤特定は、誤った近似を行っているということを意味しており、関心のある因果効果の推定結果にバイアスを生じさせます。よって、因果効果の不偏な推定のためには識別可能条件の成立に加えて、傾向スコアモデルが正しく特定されていることも必要です。
※4 Rosenbaum&Rubin (1983) 参照
・周辺構造モデルの指定がなぜ必要か
ここまで読まれた方の中には、「周辺構造モデルがどこにも登場していないじゃないか」と思われた方もいらっしゃるかと思います。これは前のセクションで想定した治療が二値変数であったため、わざわざ周辺構造モデルを指定する必要が生じなかったためです。そこで周辺構造モデルの導入のために、E[Y|A=a]をその一致推定量で層内での標本平均を用いて推定するという状況を、治療Aが(i)離散である場合、(ii)連続である場合、に分けて考えてみます。なお、識別可能条件はすべて成立しているものとします。
(i) 治療Aが離散
まず、これまで議論を行ってきたように治療Aが二値である場合、推定対象はE[Y|A=1]とE[Y|A=0]の2つです。ここで、被験者が治療群(A=1)・対照群(A=0)に偏っていないとすれば、E[Y|A=1]とE[Y|A=0]は、それぞれの群内でのアウトカムYの平均値(標本平均)によって一致推定されます。では、治療Aが二値ではなく3値以上の離散値をとる場合はどうでしょうか。まず、推定対象であるE[Y|A=a]は治療値の数だけ存在します。つまり、層内での算術平均だけを用いて単純に推定する場合、極端な話にはなりますが各層に被験者が1人でもいれば推定対象であるE[Y|A=a]の個数がサンプルサイズを超えない限り推定が可能です(e.g., サンプルサイズ nを10とすると最大で10つの治療値を取りうる治療までE[Y|A=a]を推定可能)。しかし、治療がとりうる値が増えれば増えるほど実際にその値を取る人数(カテゴリー内の総数)は減少し、統計学的には推定値の分散および信頼区間は大きくなりますので、正確な推定という観点では各層内の人数が1人である場合はいうまでもなく、数人程度では土俵に立っていないことは明らかかと思います。
(ii) 治療Aが連続
薬剤の投薬量といったようにある治療Aが連続である場合はどうでしょうか。当然ながら取りうる治療レベル、およびE[Y|A=a]は無限に存在し、明らかに研究対象集団のサイズを超えることとなります。つまり、E[Y|A=a]はそもそも単純な算術平均では推定できません。
周辺構造モデル
上記の2つの状況をまとめると、治療変数が離散多値、もしくは連続である場合には、E[Y|A=a]の推定が不可であったり推定精度が難しくなります。ここで例えば、連続である治療Aに対するYの平均E[Y|A]が、A=0のある値α0から、Aの1単位あたりβ0だけ増加することが何かしらの方法で分かるとします。つまり、E[Y|A]=α0+β0a という周辺期待値に関する等式(E[Y|A]が線形に増加するという制約)が真であり、かつそれが既知であるものとします。すると、その数が無限に想定されたE[Y|A=a]は、α0とβ0という2つのパラメータによって表現されるため、それらを推定することが出来れば任意のE[Y|A=a]を推定することが可能です(e.g., E^[Y|A=100]=α^0+100×β^0)。このパラメータの推定は因果的な理論とは別であり、線形代数の枠組みの中で扱われます(e.g., 最小二乗法)。また、一般的な最小二乗推定のような推定手法では、すべてのデータを用いて最もフィッティングの良い直線を求めるため、ある治療レベルA=aにおけるYの平均E[Y|A=a]はA≠aである被験者のアウトカムの情報も用いて推定されること、つまり、データがE[Y |A=a]の推定のために十分でないことを数学的な制約(パラメトリックモデル)を置くことで解決していることも重要なポイントです。ただし、モデルは無数に考えることが可能であり、それぞれのモデルがデータに対して課す制約もまた様々であるため、指定したモデルが真のモデル(ここではE[Y|A]=α0+β0a)と一致している(モデルの誤特定が存在しない)ことが、モデルを用いた因果効果推論を行っていくうえでは必要になります。なお、やや発展的な内容になりますが、二値である治療変数Aに対してE[Y|A]=α0+β0aというモデルを課すことはE[Y|A=1]とE[Y|A=0]の差が単にβ0であるということを示しているにすぎず、データの構造に対してなんら制約をおいていません。このように推定対象の個数がモデルにおける未知パラメータの個数と一致している場合、モデルは飽和している(saturatedである)といい、そのモデルを飽和モデル(saturated model)と言います。一方、同じE[Y|A]=α0+β0aというモデルであっても、推定対象の個数よりも未知パラメータの個数が少なくなる状況(e.g., 10つのカテゴリーを持つ治療A)ではデータの構造に数学的な制約がおかれず、モデルは飽和しません(unsaturated)。
さて、上記で例示したモデルは、あくまでE[Y|A=a]という現実世界で観測されるデータに対する数学的な制約でした。これに対し、周辺構造モデル(marginal structural models)というのは一般には観測されない潜在的な世界におけるアウトカム、潜在アウトカムYaの周辺期待値に対するモデルです。つまり、同じくA=0のある値α0から、Aの1単位あたりβ0だけ増加するという制約を与える、E[Ya]=α0+β0aとE[Y|A]=α0+β0aというモデルは、考えている世界が異なるという点に注意が必要です。この潜在的な世界と観測される世界をつなぐ役割を果たすのが、識別可能条件の1つである一致性(consistency)になります。
時間依存性治療に対する周辺構造モデルにおけるIPTW法
このセクションでは、時間依存性治療に対する周辺構造モデルにおけるIPTW法を解説します。議論を行うに当たり、次のように追加の記法を置きます。
- k:時点を表す添字(k = 0, 1, ..., K)
- Ak:時点kにおける二値である時間依存性治療(1: あり, 0: なし)
- A0:k = 0での治療(ベースライン治療)
- Ak = (A0, A1, ..., Ak):時点0から時点kまでの治療履歴
- AK = A:時点0から最終時点までの治療履歴
- Lk:時点kにおける時間依存性共変量(一般にはベクトル)
- L0:k = 0での共変量(ベースライン共変量)
- Lk = (L0, L1, ..., Lk):時点0から時点kまでの共変量履歴
- LK = L:時点0から最終時点までの共変量履歴
- Hk= (Ak-1, Lk) :時点kまでの治療歴、共変量歴
- Y:フォローアップ終了時点(K+1時点)で観測されるアウトカム(連続 or 二値)
そして、今回関心のある治療レジメンg = (g0(a-1,l0), ..., g0(aK-1,lK)) は静的であるとし、このとき治療レジメンg = (g0(a-1), g1(a0), ..., gK(aK-1)) = (a0, a1, ..., aK) とaのみの列となるため、単にaとして静的治療レジメンの表記を行います※5。また、時間依存性治療に関しては一意に平均因果効果は定まらず、特定のレジメンを2つ選択する必要があることから、任意の静的レジメンに対する潜在アウトカムの期待値E[Ya]を推定対象とします。
このE[Ya]の推定のために、前述の識別可能条件を以下のように複数時点に対応するように拡張します※7。各仮定が意図することは、治療が時間固定である場合と大きくは変わりません。また、時間固定である治療に対する識別可能条件の成立は、理想的なランダム化実験においてはそのデザイン上認められますが、下記の識別可能条件の成立は、各時点のランダム化を伴う逐次ランダム化実験(sequential randomized experiments)においてはそのデザインによって認められます※6。
- Consistency(一致性):If A = a for a given subject, Ya = Y for that subject for all a
- ある治療レジメンaを受けた場合の潜在アウトカムの値は、実際にその治療レジメンを受けた場合に観測されるアウトカムの値と一致する
- Sequential conditional exchangeability(逐次条件付き交換可能性):Ya ∐ Ak | hk for all regime a and all Lk
- 全ての時点において、未測定交絡が存在しないことと同義
- Positivity(正値性):P(0<P(Ak=1|Hk=hk)<1) = 1 for all a
- 各時点において特定の治療レベルを受ける確率が0 or 1になるような被験者は存在しない。
この静的レジメンに対する識別可能条件の下で、E[Ya]は以下のように展開が可能です。
\(
E[Y^{\overline{a}}]=E[YI(\overline{A}=\overline{a})W]=\frac{1}{n}\sum_{i=1}^{n}YI(\overline{A}=\overline{a})\prod_{k=0}^{K}\frac{1}{Pr(A_k|\overline{A}_{k-1}, \overline{L}_k)}\\
\)
つまり、任意の静的レジメンに対する潜在アウトカムの期待値E[Ya]は「実際にその治療レジメンを受けた人の観測されたアウトカムの値」と「共変量で条件付けた場合に実際に受けた治療レジメンを受ける確率の逆数(重み)」との積を平均した値(重み付け平均)となります。ここで、前者の「実際に治療レジメンaを受けた人の観測されたアウトカム」はデータとして得ることが出来ますが、後者の「共変量で条件付けた場合に実際に受けた治療レジメンを受ける確率」は、前のセクションにおける議論と同様に一般にはモデル(e.g., ロジスティック回帰モデル)を用いて推定する必要があります。具体的には、各時点の傾向スコアとでもいうような各時点で実際に受けた治療を受ける確率Pr(Ak=1|Ak, Lk)を推定し、それらをすべての時点にわたって掛け合わせることで実際に受けた治療レジメンを受ける確率を算出します。当然ながら、各時点でモデルを用いるという都合上、すべての時点のモデルが正しく特定されていることがE[Ya]をバイアスなく推定することの条件の1つとなります。
また、静的治療レジメンに対しては、上記の単純な重みWではなく、無条件での各時点の治療確率を分子に組み込んだ重みSW(安定化重み; Stabilized Weight)を用いることも可能です(下式参照)。Wではなく、このSWを用いることのメリットは、E[Ya]の推定にバイアスを生じさせることなく推定量の分散を抑えることが可能である点です。静的治療レジメンに対するIPTW法は、0~1の値を取る確率を時点数分だけ掛け合わせることから、単時点で治療が行われる場合よりも圧倒的に重みが発散しやすくなりますが、SWではそれが軽減されます。数学的な証明は参考文献をご参照ください。なお、本コラムでは扱わない動的治療レジメンに対してはSWは不適ですのでご注意ください。
\(
SW=\prod_{k=0}^{K}\frac{Pr(A_k|\overline{A}_{k-1})}{Pr(A_k|\overline{A}_{k-1}, \overline{L}_k)}\\
\)1つ前のセクションでは、時間固定である治療が(i)離散多値、(ii)連続、である場合には想定されるE[Ya]は膨大になり、治療の各値に存在する個人がごく少数になる、もしくはサンプルサイズを大きく上回るため、周辺構造モデルの指定が必要であることを紹介しました。これと同様の問題が時間依存性治療に対しても発生します。ただし、異なる点は治療が二値であったとしても問題が発生する点です。以前のコラムで紹介したように、静的である二値治療の治療レジメンaでは、各時点で治療を受けるか受けないかの2択になりますので、その総数は2K+1存在します。すなわち、各レジメンに被験者が均等に分岐するとしても各レジメンを実際にとる人数はn/2K+1であり、実際の観察研究等では特定のレジメンに人数が偏ることがほとんどであるためE[Ya]の推定精度はかなり厳しくなります((i)の状況に酷似)。よって、治療が二値であっても時間依存である場合には周辺構造モデルの設定が必要になります。
余談ですが、時間依存性治療に関する真の周辺構造モデルを得るのことは、変数の生成メカニズムが既知であるシミュレーションにおいても時間固定である場合よりも圧倒的に厳しくなります。これは、時間依存性治療ではある時点の治療や共変量はその前の時点の治療や共変量の影響を受ける(i.e., 変数が入れ子構造になっている)ことから、計算しなければならない条件付き分布が時点数が増えれば増えるほど膨大になるためです。特に、時間依存性共変量が時点間で因果効果を持つ場合(e.g., DAGにおいてLk-1からLkへの矢線が存在するとき)には、計算は現実的にほぼ困難です。治療時点数と離散である共変量がごく少数である場合には計算は可能かとは思いますが、現実的にはそういった状況は僅かかと思います。ただし、共変量が少数かつ離散であれば、サンプルサイズを巨大にすることで、共変量の層内平均を用いて経験的にE[Ya]の真値を求めることが可能です。
※5 gk(ak-1,lk)は時点kでの治療akを、それ以前の情報 (ak-1,lk) を用いて定める指示関数であり、治療レジメンは決定論的であることも暗黙的に仮定している
※6 正確にはサンプルサイズが無限(n→∞)であるときに成立
SASでの実装
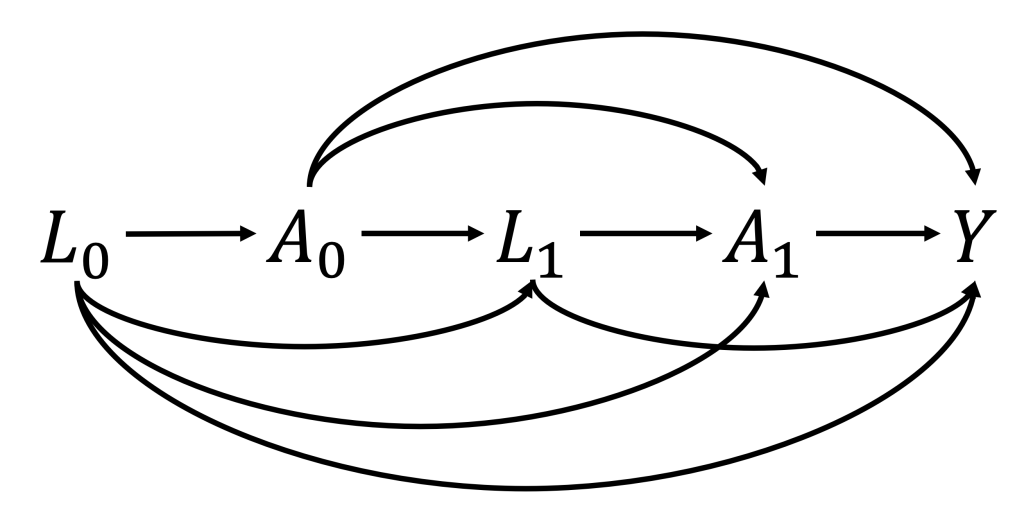
ここからはSASでの実装に移ります。まず、治療は2時点で行われるものとし、変数の真の構造は以下のDAGで表されるとします。つまり、ある時点の治療はそれ以前の共変量と治療の影響を受けており、かつアウトカムに対しても因果効果を持つとします(共変量ベクトルに関しても同様)。
データの生成は以下のプログラム・コードによって行います。
/* データのシミュレーション */ data df; call streaminit(12345); /* シード値の指定 */ keep ID Gender Age Press TG; N=5000; /* サンプルサイズの指定 */ do i=1 to N; /* 変数の生成 */ ID = i; Gender = rand('BINORMINAL',0.5,1); Age = round(20+45*rand('UNIFORM'),1); if Gender=0 then Press = round(rand('NORMAL',100,20)+0.6*Age,1); if Gender=1 then Press = round(rand('NORMAL',110,20)+0.6*Age,1); TG = round(rand('NORMAL',90,15) +0.6*Age + 10*Gender,1); output; end; run; /* t=0での治療変数の追加 */ data df; set df; call streaminit(12345); /* シード値の指定 */ keep ID Trt0 Gender Age Press TG; PS0_True=logistic(0.5+0.8*Gender-0.03*Age);/* t=0での真の傾向スコアモデル */ Trt0 = rand('BINOMINAL',PS0_True,1); run; /* t=1での治療変数、アウトカムの追加 */ data df; set df; call streaminit(12345); /* シード値の指定 */ keep ID Trt0 Trt1 Outcome Gender Age Press TG; PS1_True=logistic(0.6-0.4*Gender-0.01*Age+0.5*Trt0+0.01*Press-0.015*TG);/* t=0での真の傾向スコアモデル */ Trt1 = rand('BINOMINAL',PS1_True,1); epsilon = rand('NORMAL',0,10); Outcome = round(130 - 10*Trt0 - 4*Trt1 +Gender +Age +Press+ TG+ epsilon,1); run; /* 変数の順序変更 */ data df; format ID Trt0 Trt1 Outcome Gender Age Press TG; set df; run; |
そして、今回は周辺構造モデルをE[Ya0, a1] = β0 + ψ0a0 + ψ1a1として考えます。つまり、各時点での治療効果は加法的に潜在アウトカムの期待値に因果効果を与えており、治療間や治療と共変量との交互作用はないものと仮定します。上記の周辺構造モデルを想定すると、k=0,1でともに治療を受けた場合にともに治療を受けなかった場合と比べてどの程度平均的に因果効果があるかは、下記のようにψ0, ψ1という2つの因果パラメータに分解されます。この因果パラメータをIPTW法によって推定します。
- E[Ya0=1, a1=1] - E[Ya0=0, a1=0] = (β0 + ψ0 + ψ1) - β0 = ψ0 + ψ1
- ψ0: k=0(ベースライン)での治療による因果効果
- ψ1: k=1での治療による因果効果
次に、上記のデータを用いて周辺構造モデル、およびIPTW法の適用しますが、我々が行うステップは大きく2つ、細かく見ると3つあります。なお、想定する治療レジメンは静的であるため、通常のweightではなくstabilized weightを重みとして用います。
- 各個人への重みの推定
- 分子
- 各時点の治療変数の単純な割合によって推定
- 分母の推定
- 各時点で個人が実際に受けた治療を受ける確率をロジスティック回帰モデルによって推定(LOGISTIC procedure)
- 分子
- 指定した周辺構造モデルにおけるパラメータ推定
- 想定する周辺構造モデルに対して、2で計算した重みを用いて重み付き回帰を実施(GENMOD procedure)
上記を行うプログラミング・コードが以下になります。
/*各時点の傾向スコアの算出*/ /*t=0*/ proc logistic data=df descending; class Gender(ref="0") /param=ref ref=first; model Trt0=Gender Age; output out=df predicted=PS0; run; /*t=1*/ proc logistic data=df descending; class Gender(ref="0")/param=ref ref=first; model Trt1=Gender Age Trt0 Press TG; output out=df predicted=PS1; run; /*SWの分子の計算*/ proc logistic data=df descending; model Trt0=; output out=df predicted=Pr0; run; proc logistic data=df descending; class Trt0/param=ref ref=first; model Trt1=Trt0; output out=df predicted=Pr1; run; /*各個人のweightの計算*/ data df_wt; set df; if Trt0=1 then wt0=Pr0/PS0; else wt0=(1-Pr0)/(1-PS0); if Trt1=1 then wt1=Pr1/PS1; else wt1=(1-Pr1)/(1-PS1); wt=wt0*wt1; run; /*因果パラメータの推定*/ proc genmod data=df_wt; class ID Trt0 Trt1/param=ref ref=first; model Outcome = Trt0 Trt1/ error=normal link=id; weight wt; repeated subject=ID/ type=ind; run; |
上記を実行結果が以下です。ψ0, ψ1の推定結果が赤枠の部分です。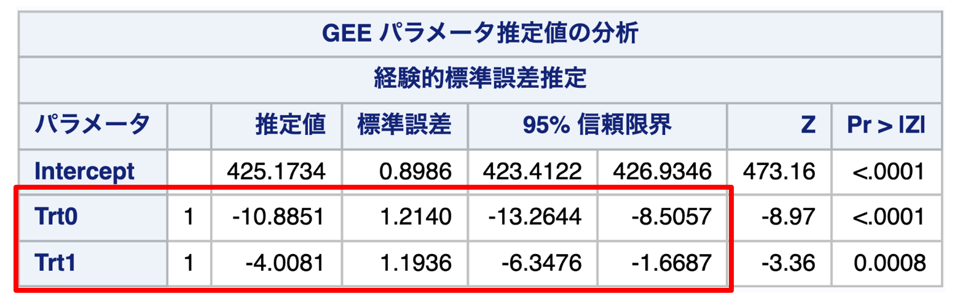
なお、治療変数の生成過程で設定したモデルをパラメータの推定においても用いているため、重みの推定に関するモデル(各時点の治療確率モデル)の誤特定は存在しません。ただし、周辺構造モデルの指定に関しては真の周辺構造モデルの特定を行っていないため、その部分の誤特定によるバイアスは含まれている可能性があります。
まとめ
本コラムでは、時間依存性治療(特に静的治療レジメン)に対する周辺構造モデルとIPTW法について簡単に紹介を行いました。二値治療に対する静的治療レジメンは、2の時点数乗通り存在し、各レジメンを実際にとる被験者はごく少数になるため、周辺構造モデルという数学的な制約を潜在アウトカムの周辺分布(期待値)に対して設定する必要があります。周辺構造モデルのパラメータ推定を行うのがIPTW法であり、この方法では一般に各時点での治療確率モデルを特定する必要があります。すなわち、時間依存性治療に関する因果効果を周辺構造モデルにおけるIPTW法によってバイアスなく推定するためには、以下の仮定がすべて成立する必要があります。
- 識別可能条件(一致性、逐次条件付き交換可能性、正値性)
- 周辺構造モデルが正しく特定されている
- 各時点の治療確率モデルがすべて正しく特定されている
時間固定である治療と比較すると、時間依存性治療に対して必要となる仮定は大きく増えます。また、IPTW法において重みが発散することが治療が単時点で行われる場合よりも明らかに多くなることや、シミュレーション研究であっても真の周辺構造モデルを得ることが難しいなど、仮定の妥当性とは別の様々な問題が存在します。そのため、理解や統計ソフトでの実装は比較的容易であるものの、ベーシックな周辺構造モデルにおけるIPTW法を解析方法として採用する場合には、手法の性質を含めた十分な議論が必要かと思います。
Reference
- Rosenbaum, Paul R., and Donald B. Rubin. "The central role of the propensity score in observational studies for causal effects." Biometrika 70.1 (1983): 41-55.
- Hernán MA, Robins JM (2020). Causal Inference:What If. Boca Raton: Chapman & Hall/CRC.
- Hernán MA & Robins JM (2009). Estimation of the causal effects. In: Fitzmaurice G, Davidian M, Verbeke G, & Molenberghs G, eds. Longitudinal Data Analysis. Boca Raton: Chapman & Hall/CRC.
- Robins, James M., Miguel Angel Hernan, and Babette Brumback. "Marginal structural models and causal inference in epidemiology." Epidemiology 11.5 (2000): 550-560.
- Shinozaki, Tomohiro, and Etsuji Suzuki. "Understanding marginal structural models for time-varying exposures: pitfalls and tips." Journal of epidemiology 30.9 (2020): 377-389.