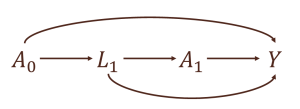注）　本コラムは『経時的に変化する治療（Time-varying treatments）に対する因果推論』と題した以前のコラムを、時間依存性治療に関する部分と周辺構造モデルにおけるIPTW法に関する部分に分割し、内容の追加と修正を行い再構成したものの一部となります。

 

はじめに

多くの統計的因果推論に関する書籍や文献では、ある治療^※1が単時点で行われる場合の因果効果の推定手法について紹介がされています。しかし、治療が複数の時点にわたって実施され、その一連の治療による効果に興味があるという状況も存在するかと思います。例えば、新型コロナワクチンの接種が我々に身近な例として挙げられ、これ以外にも顧客に対する商品のレコメンデーションなど医学分野に限らず様々な例が挙げられます。

正確な定義は後述しますが、上記で挙げたような複数の時点において実施され、かつ各時点での値が異なりうる（時間経過とともにとる値が変化しうる）治療は、時間依存性治療（time-varying treatments）と呼ばれます。時間依存性治療に対する因果推論へのニーズは、近年の統計的因果推論という言葉自体の認知の広まりや個別化医療への関心の高まりに相まって増加しています。一方で、その統計学的理論の理解は点治療の状況と比較すると内容が高度になることや日本語での文献が少ないことからそれほど進んでいません。そこで、本コラムでは時間依存性治療に対する効果をどのように定義するか、問題となることは何か、どのように効果の推定を行えばよいかについて簡単に解説を行います。また、いくつかの代表的な推定手法についてはSASでの実装方法も併せて紹介を行います。なお、本コラムは潜在アウトカムモデルの枠組みの下での因果推論について基本的な理解があることを前提としています。適宜関連する書籍や文献、因果推論に関する連載コラムをご参照していただければ幸いです。

※1　本コラムにおいては、介入（intervention）や曝露（exposure）など他の原因となる変数を治療（treatment）と同義的に用いて構わないものとする

 

 

因果推論を行う上での治療分類（"time-fixed" or "time-varying"）

ある治療とアウトカムとの因果関係を議論する場合、治療はtime-fixed treatments（時間固定性治療）^※2、もしくはtime-varying treatments（時間依存性治療）のいずれかに分類がされます。そして、このどちらに属するかによって扱いは大きく異なります。まず、治療が時間固定（time-fixed）であるとは、対象集団におけるすべての被験者に関して、初回の治療レベルが以降のすべての時点における各々の治療レベルを決定することを指します。この状況としては大きく3つあります。

• 治療が研究開始時点でのみ行われる

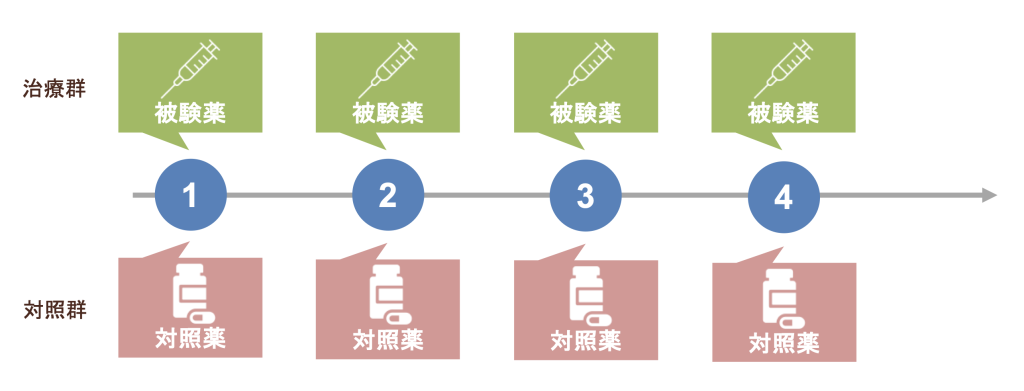
1つ目は、治療がベースラインやtime zeroとも呼ばれる研究やプロジェクトの開始時点でのみ行われる場合です。一般的な臨床試験で投与される被験薬・対照薬や、一回の投与で完全な免疫を与えるone-dose vaccine（e.g., 黄熱病ワクチン）などが実例として挙げられます。

• 初回の治療レベルが時間経過によって不変

2つ目は、初回の治療が2回目以降の治療時点においても変わらず継続的に行われる場合です。この状況の例としては、被験薬と対照薬の複数回投与が予定される臨床試験や近年いくつかの国で導入されているベーシックインカムといったものが挙げられるかと思います。

• 決定論的に各時点の治療レベルが定まる

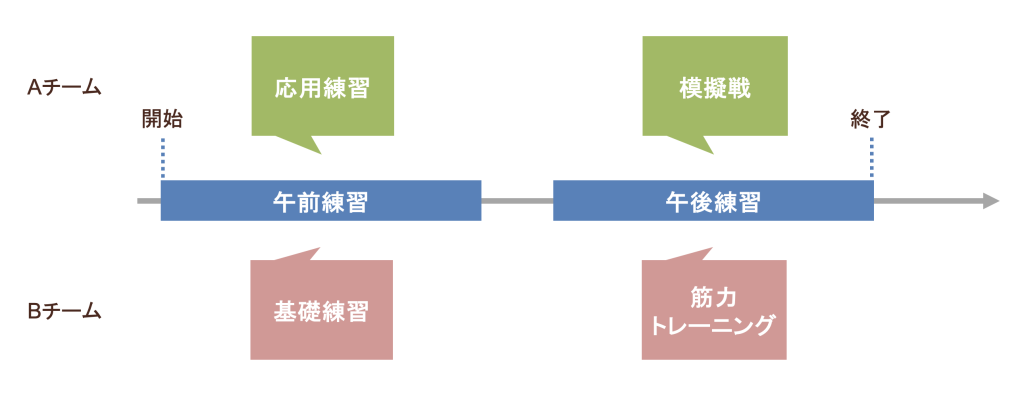
3つ目は、初回の治療レベルが決定論的にその後の治療レベルを定める場合です。すなわち、初回治療での分岐以降はそれぞれ1つの治療パターンとなる場合です。例えば、A群に割り付けられた被験者は隔週で被験薬を、B群に割り付けられた被験者は毎週対照薬を投与（初回治療が被験薬なら毎週投与、対照薬なら隔週投与）されるといった実験が1つの例として考えられます。また、Aチームに配属された選手は実践練習と模擬戦を、Bチームに配属された選手は基礎練習と筋力トレーニング（初回練習が応用練習ならその後は模擬戦、基礎練習なら筋力トレーニング）をそれぞれ1日の練習メニューとして行うといったものもスポーツの領域における例として考えられます。

上記の分類からも類推されるように、治療が複数時点で行われるとしても2, 3の状況に該当する場合には、因果推論を行う上での扱いは治療が単時点で行われる場合と変わらず、ベースライン共変量の調整に基づく手法が適用可能です。これはすべての個人に関して初回治療によって2回目以降の治療が決定されるため、後述する時間依存性交絡（time-dependent confounding）という問題が生じ得ないためです。

 

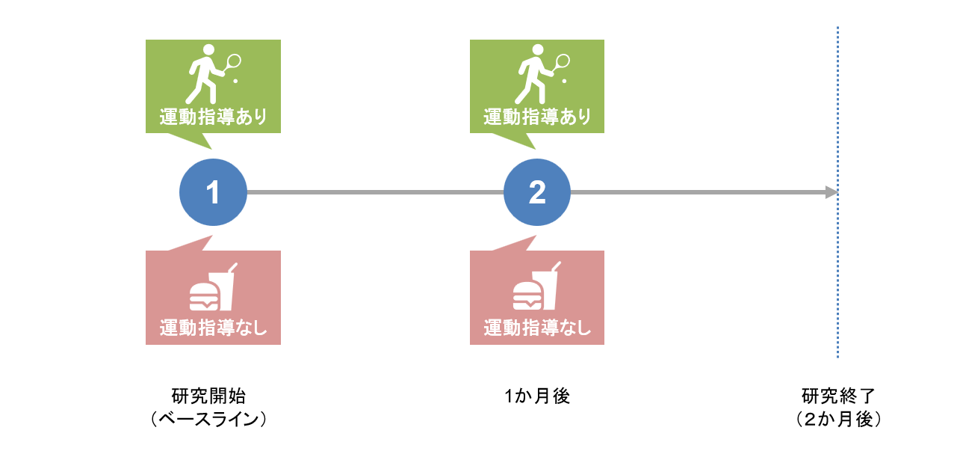
次に、時間依存性治療（time-varying treatments）とは時間固定でない治療すべてを指します。すなわち、複数時点で行われる治療であり、かつ各時点でとる値が初回の治療によって決定論的に定まらない治療が時間依存性治療にあたります。例えば、月に1回のペースで運動指導プログラムをある市において行うというプロジェクトを考えてみます。ここで、「初回指導に参加した場合は何があっても絶対に毎回参加しなければならない」や「初回指導に参加しなかった場合には絶対に以降参加できない」などといった特殊な制約がない限りは、各指導日でプログラムという2つの選択肢を市民は取ることができます。そのため、この運動指導というのは時間依存性治療にあたります。

この他にも疫学研究における喫煙や投薬量が被験者の状態によって変更される処方、検索履歴に応じて表示される広告（レコメンド）など様々な曝露、治療、介入が時間依存の例として挙げられます。ただし、特に疫学・医学分野においては本質的には時間依存であるものの、測定の実現可能性から時間固定とされる場合もあります。また、対照的に研究・プロジェクトの計画時点では時間固定であるものの、研究実施後には時間依存であるとみなされる場合もあります。それが割付の不遵守（コンプライアンス違反）が存在する場合の治療です。例えば、上記の時間固定である治療の2番目のシナリオで紹介した継続的に被験薬と対照薬（実薬）を投与するという臨床試験においては、試験に参加する被験者が何らかの理由（e.g., 副作用の発現）で治療法を切り替える場合があります。このような状況においては、本来は時間固定であった治療を時間依存性治療とみなして解析（補正）を行うことが可能です。

※2　執筆時点で対応する定訳が存在しないという筆者の認識であるが、本コラムにおいては時間固定性治療という訳をあてる

 

 

治療レジメン（treatment regime）

ここまでは因果推論を行う上での治療分類について紹介を行いましたが、以降では治療レジメンとその分類について紹介と解説を行います。これらは、因果効果の定義やデータを用いて効果を推定する（識別のために必要な仮定を検討する）場合に非常に重要になります。ここから先は数学的な内容も入りますので、以下のように記法をおきます。基本的にはアルファベットの大文字は確率変数を、小文字はその実現値を指しています。

• k：時点を表す添字（k = 0, 1, ..., K）
• A_k：時点kにおける二値である時間依存性治療（1: あり, 0: なし）
  • A₀：k = 0での治療（ベースライン治療）
  • A_k = (A₀, A₁, ..., A_k)：時点0から時点kまでの治療履歴
  • A_K = A：時点0から最終時点までの治療履歴
•  L_k：時点kにおける時間依存性共変量（一般にはベクトル）
  • L₀：k = 0での共変量（ベースライン共変量）
  • L_k = (L₀, L₁, ..., L_k)：時点0から時点kまでの共変量履歴
  • L_K = L：時点0から最終時点までの共変量履歴
• Y：フォローアップ終了時点（K+1時点）で観測されるアウトカム（連続 or 二値）

上記の記法をおくと、例えば、研究を通じてずっと治療を受けた続けた被験者の治療履歴はA = (1, 1, ..., 1) であり、治療をずっと受けなかった被験者の治療履歴はA = (0, 0, ..., 0) と表されます。このような被験者は極端な例になりますが、他の被験者に関しても1と0の列として治療履歴を表すことが可能です。

さて、時間固定である治療では効果をどのようなスケール（e.g., 加法的, 乗法的）で見るかを定めれば、ある1つの時点（初回治療）での潜在アウトカムの比較（e.g., E[Y^a=1] - E[Y^a=0]）によって明らかに”因果効果”というものを定義できました。しかし、ここで時間固定性治療と時間依存性治療の違いとして重要なことは、ある時点kでの潜在アウトカムの対比ではもはや時間依存性治療の効果は定義できないことです。例えば、平均因果効果を加法的なスケールでの潜在アウトカムの対比E[Y^a_k=1] - E[Y^a_k=0]とすると、これはあくまである1つの時点kでの治療A_kの効果を定量化しているに過ぎず、時点0から時点Kまでのすべて時点における時間依存性治療の効果を表しているわけではありません。

そこで、時間依存性治療の因果効果の定義をしていくためには治療レジメン（treatment regimes）^※3というものをまず議論する必要があります。定義から述べると、治療レジメンとは治療が行われる各時点kにおけるの治療の割付ルールです。そして、この治療レジメンはその割付ルール（治療レベルの定まり方）によって、静的（static）もしくは動的（dynamic）、決定論的（deterministic）もしくは確率的（random）であるかの2×2の計4つの区分に分類され、いずれに属するかによって議論や効果の推定のために必要となる仮定（識別可能条件）が異なります。ただし、我々が因果効果を検討するたいていの状況においては治療レジメンは決定論的であるため、次のセクションではまず決定論的なレジメンに限定をして静的 / 動的な治療レジメンの紹介を行います。なお、治療レジメンとは仮想的な割付ルールであり、実際に受けた一連の治療を表す治療履歴とは概念としてそもそも異なります。この点に注意して以降の内容に進んでいただければ幸いです。

※3　分野や状況によってはregime以外にもstrategy, plan, protocol, policyなどと呼ばれる

 

 

静的 / 動的治療レジメン

静的、もしくは動的な治療レジメンの紹介を行うために、まず治療レジメンをg = (g₀(a_-1,l₀), ..., g₀(a_K-1,l_K)) とおきます。ここで、g_k(a_k-1,l_k)は時点kでの治療a_kを、それ以前の情報 (a_k-1,l_k) を用いて定める指示関数です。静的（static）、もしくは非動的（non-dynamic）な治療レジメンとは、各時点の治療a_kを定めるg_k(a_k-1,l_k) がそれまでの共変量歴 l_k に依存しない治療レジメンを指します。すなわち、g = (g₀(a_-1), g₁(a₀), ..., g_K(a_K-1)) = (a₀, a₁, ..., a_K) となります。静的治療レジメンでは、単純に各時点で治療を実施するかしないかという2択になるため、その数（パターン）は2^K+1通り存在します。例えば、二値である時間依存性治療が毎月実施されうるという状況を考えてみると、以下のようなものが静的治療レジメンとして挙げられます。

• 常に治療を実施する（always treat）：g = (1, 1, ..., 1) = 1
• 常に治療を実施しない（never treat）：g = (0, 0, ..., 0) = 0
• 月毎に治療実施の有無を切り替える：g = (1, 0, 1, 0, ..., 1) or g = (0, 1, 0, 1, ..., 0)
• 途中で治療を取りやめる：g = (1, 1, 1, 0, 0, ..., 0) など

治療レジメンに関しては、単時点で治療が行われる場合と同様に各レジメンgごとに潜在アウトカムY^gを考えることが可能です。しかし、静的治療レジメンに対する潜在アウトカムは2^K+1通り存在するため、因果効果の定義は一意に定まらず、その効果に興味があるレジメンを選択する必要があります。例えば、「常に治療を実施した場合には、常に治療を実施しなかった場合と比べてどの程度平均的に効果があるのか」に興味がある場合には、E[Y^g=1] - E[Y^g=0] が加法的なスケールでの平均因果効果として定義されます。また、多数存在する治療レジメンのうち少なくとも2つのレジメンg, g’ に関してE[Y^g] ≠ E[Y^g’] となれば、時間依存性治療A_kはアウトカムYに対して平均的に因果効果を持つとされます。なお、静的治療レジメンは上記で示したように単にaの列として表記することが可能です。そこで多くの文献に習い、以降では広く治療レジメン全体を言及する場合にはgとして、静的・動的レジメンに関して言及する場合にはそれぞれa, gとして表記を行います。

次に、動的（dynamic）な治療レジメンとは、各時点の治療a_kがそれまでの共変量歴 l_k にも依存して定まる治療レジメンを指します。この動的治療レジメンの例としては様々なものが考えられますが、各月で測定されるある検査値（e.g., HbA1c）の値が閾値x（e.g., 8%）を上回った場合に限り治療を実施し、治療を実施したのであればそれ以降も継続的に治療を実施し続けるといった治療の決定ルールが1つの例として挙げられます。各被験者に与えられる一連の治療割付は、治療レジメンが静的である場合には研究開始時点で明示できるものの、動的である場合には研究開始時点では明示できません^※4。これは、共変量歴を参照して各時点の治療が適応的に定まるためです。また、上記の例におけるxに様々な値が入りうることや治療の決定に複数の条件を用いてもよいことからも分かるように、動的治療レジメンの数は静的治療レジメンで与えられる2^K+1より一般には多くなります。

なお、上記では暗黙的に治療レジメンは決定論的であることを仮定しましたが、確率的な治療レジメンというものもあります。一言でいえば、この2つの治療レジメンの違いは個人に割り付けられるものの違いです。決定論的な治療レジメンでは治療変数の実数値（e.g., 0 or 1）が、確率的な治療レジメンでは治療を受ける確率（e.g., 0.7 or 0.3）がそれぞれ与えられます。

※4　数学的な表記は可能であり、ここでの例はg_k(a_k-1,l_k) = I(a_k-1=1 or l_k>x)として表現される（Iは条件に合致する場合には1を、合致しない場合には0をとる指示関数）

 

 

時間依存性交絡の問題

以前のセクションでは治療レジメンというものについて紹介をしました。そして、この治療レジメンの比較によって時間依存性治療の因果効果が定義されましたが、この効果を推定するためには一部の研究デザイン^※5を除き、時間依存性交絡（time-dependent / time-varying confounding）と呼ばれる問題に適切に対応する必要があります。この問題を直感的に理解するために、まず単時点で治療が行われる場合の因果推論でのいくつかの変数の扱いを簡単に振り返ります。

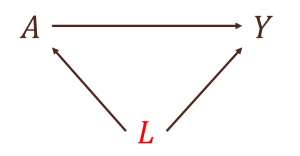
• 交絡因子（confounders）L

あるtime-fixedである治療Aが興味のあるアウトカムYに及ぼす平均因果効果E[Y^a=1] - E[Y^a=0]を推定する場合、交絡^※6を十分に制御する必要があります。この交絡を制御するに足る変数が交絡因子Lであり、交絡因子は典型的には下図のように治療AとアウトカムYの共通原因として表されます。ここで、この交絡因子Lを調整（条件付け）しない場合には因果効果の推定結果にバイアスが生じてしまいます。

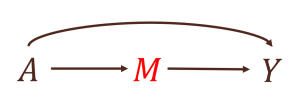
• 中間変数（mediators）M

同様の状況において、治療Aから影響を受け、かつアウトカムYに影響を与える中間変数Mが存在するとします。ここで、治療AがアウトカムYに及ぼす総合効果に興味がある場合には、この中間因子Mは解析に含むべきではありません。これは、この中間因子Mで調整（条件付け）を行ってしまうと間接効果（A→M→Y）が推定結果から除かれてしまうためです^※7。

 

次に、時間依存性治療A_kが二時点（k=0, 1）で実施され、それらがアウトカムYに及ぼす平均因果効果 E[Y^{a₀=1, a₁=1}] - E[Y^{a₀=0, a₁=0}] に興味があるとします。そして、正しい変数間の関係が以下のDAGで与えられているとします。

ここで注目していただきたいのはL₁です。上記のDAGをよく見ると、L₁は以下の2つを同時に満たす変数であることが分かるかと思います。

• A₁とYの交絡因子（A₁←L₁→Y）
• A₀とYの中間因子（A₀→L₁→Y）

前述のように交絡因子は解析において調整する（条件付けを行う）必要があります。一方で中間因子は解析において調整する（条件付けを行う）と間接効果が除かれてしまうため調整を行うべきではありません。つまり、L₁を条件付けても付けなくても因果効果の推定結果にバイアスが含まれてしまうという二項対立の状況が上記のDAGで発生しており、条件付けに基づく方法である回帰や標準化、マッチングといった標準的な因果効果の手法を用いることは妥当ではありません。このような問題を時間依存性交絡^※8と呼び、L₁のように①前の時点の治療の影響を受け^※9、②次の時点の治療とアウトカムの交絡因子である、という2つの条件を満たす変数は時間依存性交絡因子（time-varying / time-dependent confounders）と呼ばれます。そして、この例からも類推されるように、上記の推定手法は時間依存性治療に対しては一般に適しません^※10。

※5　代表的な研究デザインとして逐次ランダム化実験（sequential randomized experiments）があげられる
※6　E[Y^a=1] ≠ E[Y|A=1] and/or  E[Y^a=0] ≠ E[Y|A=0]
※7　総合効果（A→Y, A→M→Y）が直接効果（A→Y）と間接効果（A→M→Y）が分けて推定される
※8　正確・数学的な定義については、Hernán MA, Robins JM (2020),pp260を参考のこと
※9　もしくは前の時点の治療と共通の原因を持つ
※10　L₁→A₁がなければ（No feed backと呼ばれる後述の②の仮定が満たされなければ）、条件付けに基づく手法で妥当な結果を得ることは可能であるが、この仮定を認めることが非現実的となることが多い

 

 

時間依存性治療の因果効果の推定手法

上記で説明したように、時間依存性治療に対しては一般に時間依存性交絡の問題が発生するため、条件付けに基づく手法（e.g., 回帰、層別化、マッチング）では効果の推定結果にバイアスが含まれます。そこで用いられるのが、ハーバード大学のJames M. Robins教授により体系化されたg-methodsと総称される次の3つの手法です (Robins' g-methods)^※11 。

• G-computaion algorithm formula ("g-formula")
• Inverse probability of treatment weighting (IPTW) of marginal structural models (MSMs)
• G-estimation of structural nested models (SNMs)

上表が各手法の特徴を簡単にまとめたものになりますが、実務を行う上では結論としてどの手法を用いるべきかということが1つ気になることかと思います。残念ながらこの点については現時点で一貫した答えはなく、各手法の特徴等から総合的に判断していく必要があります。各手法の統計学的理論、直感的な理解、およびSASでの実装方法については、それぞれ独立したコラムとして今後紹介を行います。また、時間依存性治療の因果効果の推定にあたっては、g-methods以外にもいくつかの手法が提案されており^※12、興味がある方は添付のリンクからご参照いただけると幸いです。

※11　本コラム中では言及しないが、静的/動的治療レジメンに対する因果効果の識別のためにはそれぞれ異なる仮定（識別可能条件）が要求される

※12　Edward H. Kenneyによる提案など

 

Reference

• Hernán MA & Robins JM (2020). Causal Inference:What If. Boca Raton: Chapman & Hall/CRC.
• Hernán MA & Robins JM (2009). Estimation of the causal effects. In: Fitzmaurice G, Davidian M, Verbeke G, & Molenberghs G, eds. Longitudinal Data Analysis. Boca Raton: Chapman & Hall/CRC.
• Naimi AI, Cole SR, & Kennedy EH. (2017). An introduction to g methods. International journal of epidemiology, 46(2), 756-762.
• Kennedy EH. (2019). Nonparametric causal effects based on incremental propensity score interventions. Journal of the American Statistical Association, 114(526), 645-656.