はじめに
データに基づいた意思決定が必要とされる場面が近年ますます増えており、そういった際には、データからいかに因果関係を導き出すかが非常に重要な問題です。”因果”を統計学的に捉え、いかにしてそれに迫るかは、統計的因果推論として体系化がなされています。SAS Blogでは、前回の記事からこの統計的因果推論に関する連載コラム・シリーズが始まりました。
因果関係を統計学的に導くことを目的とする統計的因果推論には、主に2つの枠組みがあります。1つは潜在アウトカムを用いるRubin流の考え方、そしてもう1つが構造的因果モデルを用いるPearl流の考え方です。これら2つの考え方は相反するものではなく、Pearl流の因果推論では、ある変数の特徴とそれらの関係を記述するために構造的因果モデル (SCM; Structural Causal Model) が用いられています。このSCMには対応するグラフィカル因果モデルがそれぞれ存在しており、その際に使用されるのが有向非巡回グラフ (DAG; Directed Acyclic Graph)※1です。このDAGはRubin流の因果推論においても、変数間の関係を視覚的に理解するために補助的に利用がされています。本コラム・シリーズでは前者の潜在アウトカムの枠組みでの因果推論について紹介を行います。今回は特にその根底となる潜在アウトカムについて、また、それを用いた因果関係の定義について説明します。
※1 補足資料を参照
相関関係と因果関係
相関関係とは、ある2つの変数において、一方が増加するにつれてもう一方も増加(減少)する傾向があるという双方向の関係を意味しています。これに対し因果関係とは、ある2つの変数のうち、一方の操作可能な変数(原因)の値を変化させる(介入を行う)と、もう一方(結果)の値が変化するという、原因から結果への一方向的な関係です。これらの関係の違いを理解することは社会生活を送る上で非常に重要です。例えば、相関関係がある有名な例として、年収と血圧の関係があります。この2つの変数の間には正の相関関係(年収が高くなるほど血圧が高い傾向)があります。しかし、年収を上げるために血圧を上げる(Ex, 暴飲暴食を行う)ことは妥当でしょうか。もしくは、血圧を下げるために年収を下げる(Ex, 転職をする)ことは受け入れられることでしょうか。おそらく多くの読者の方の意見は「No」であるかと思います。この例からも察することができるように、相関関係と因果関係の存在とその方向というものは必ずしも一致しません。また、これらの関係を混同することは大きな不利益につながる可能性があります。上記の例であれば、真には血圧の増加は年収増加に対して因果的な効果を持たないのにも関わらず年収を上げるために無駄に暴飲暴食を行ってしまうことで、結果として不健康につながる可能性があります。
このように興味の対象が因果関係、因果効果である場面は比較的多く存在します。統計的因果推論 (causal inference) とはこれらを形而的、哲学的にではなく、統計学的に考える学問分野です。また、単に因果推論と言われる場合もあり、コラム中で単に因果推論と呼称した場合には、統計的因果推論を意味していることにご注意ください。データから因果効果を推定するために「傾向スコア」を用いた手法など様々なものが用いられています。しかし、これらの手法は適用さえすれば因果効果を適切に推定することができるというわけではありません。因果推論を行うにあたっては因果関係を検討する集団はどういった集団であるか、考える因果効果はどのような介入の効果であるかといった因果的な疑問 (causal question) を明確にすることがまず重要です。その上でデータへの手法の適用があります。また、それぞれの手法は異なる仮定を必要とするため、無条件で因果効果を求めることはできず、その仮定が目の前にあるデータに対してどの程度成立するものであるかといった議論も必要です。 加えて、推定する対象が手法間で異なるといった点や真の関係をゆがませる要因は何が想定されるのかなど、他にも様々な事を考慮する必要があり、慎重に議論を行っていくことが大切です。本コラムでは潜在アウトカムの枠組みでの因果推論の理論(考え方)と、一部の因果効果の推定手法についてのみ取り扱いますが、現実的にはそのような総合的な議論が重要です。
本コラムにおける用語
今回のコラムでは、心臓移植とその5日後の生存の間の因果関係を具体例として考えます。すなわち、心臓移植という介入が5日間の生存というアウトカムに対して、因果効果を持つかどうかを検討します。医療の分野では原因として考える要因を介入 (intervention) や処置 (treatment) 、曝露 (exposure)、結果変数のことをアウトカム (outcome) と呼ぶことが一般的であり、このコラム・シリーズでは、具体例として主に医療関連の話題を取り上げるため、基本的にはこのような呼称を行います。経済・金融系の分野では、因果効果があるかどうか検討したい要因が施策等である場面があるかと思いますが、因果推論の理論に関して変わりはないので、本コラムの例を読者の方がそれぞれ抱えている疑問に置き換えて考えるとよいでしょう。ただ、今後紹介する因果推論に関する様々な仮定の妥当性や分析に用いられるデータの特徴は、それぞれの分野によって異なりますので、その点ご理解ください。
潜在アウトカムによる因果効果
それでは早速、例を用いて潜在アウトカムとは何か、因果関係とは何かを考えていきます。具体的には心臓移植(介入)が5日後の生存(アウトカム)に対して因果的な効果があるのかどうかを考えます。この関係を検討するために、まずゼウスとヘラというある2人に対し、ともに介入を行うことを想定し、何らかの方法で以下の結果が得られたものとします。
ゼウスは1月1日に心臓移植を受けると、その5日後には死亡している。
ヘラは1月1日に心臓移植を受けると、その5日後は生存している。 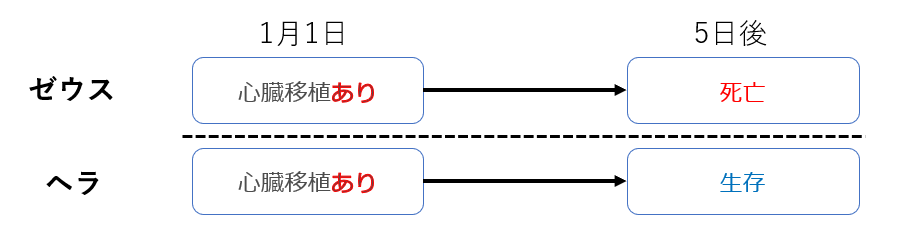
このもしもの結果(介入を行う場合の結果)が分かったとき、心臓移植はゼウスとヘラの5日間の生存に対してそれぞれ因果効果を持つと結論付けることは可能でしょうか。一見すると、ゼウスは心臓移植後に死亡し、ヘラは生存していますので、ゼウスに対してはnegativeな因果効果(心臓移植により死亡した)、ヘラに対してはpositiveな因果効果(心臓移植により生存した)があったように見えます。しかし、その結論は正しいのでしょうか。もしかすると心臓移植を受けずとも、ゼウスは5日後には亡くなり、ヘラは生きていたのかもしれません(結果は変わらなかった)。もしくは心臓移植を行わなければ、逆にゼウスは生存し、ヘラは亡くなっていたのかもしれません。つまり因果効果があるかどうかについては、この結果だけでは判断することはできません。
では、どのような状況であれば因果関係かどうかを判断することができるでしょうか。その1つのアイディアがもし介入を受けなかったらどのような結果が得られたのかを考えることです。実際にはゼウスもヘラも介入を受けるか受けないかのいずれかしか取り得ないため、必ずどちらか一方の結果は現実的には得られない(反事実)ものとなってしまいますが※2、先ほどと同様に何かしらの方法でその場合の結果を知ることができたと仮定し、それぞれの場合の結果を比較するわけです。そして、それらの値が異なるのであれば介入の因果効果があるとし、同一であるのならば因果効果がないと判断します。  ゼウスとヘラに関しては、以下のようなifの結果が得られたとします。
ゼウスとヘラに関しては、以下のようなifの結果が得られたとします。
ゼウスは1月1日に心臓移植を受けないと、その5日後は生存している。
ヘラは1月1日に心臓移植を受けないと、その5日後は生存している。
先程の結果も含め、介入を受ける場合と受けない場合の結果をまとめたものが下図です。
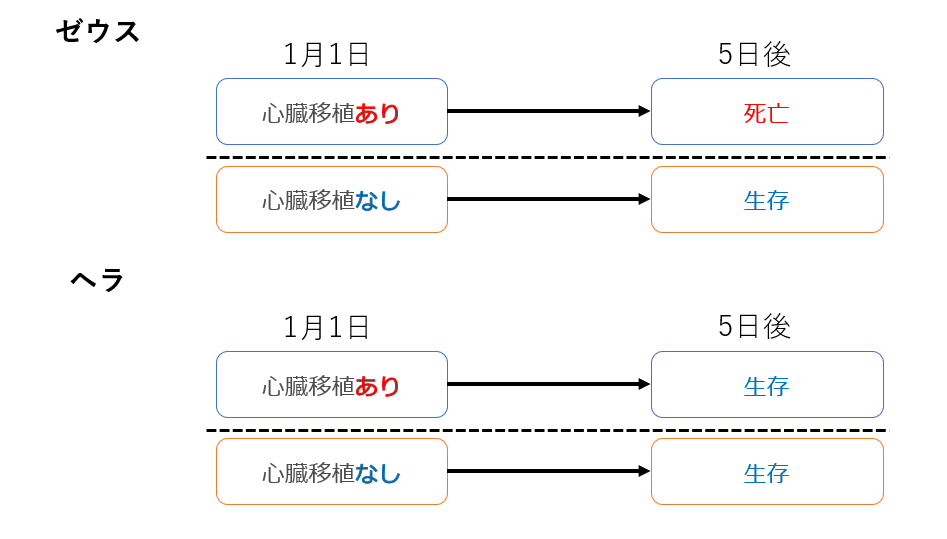
介入を受けない場合の結果が得られたことにより、心臓移植はゼウスに対しては5日後の生存に対し因果効果を与えた(ネガティブな効果)、ヘラには因果効果を与えなかった(介入があってもなくても結果は同じ)と判断することができます。おそらく、この判断に関しては読者の方々も特に異論はないかと思います。この例のように、ある介入を受けた場合のifの結果のことを潜在アウトカム (potential outcomes) 、ないしは反事実アウトカム (counterfactual outcomes) と呼びます※3。なお、今後は潜在アウトカムで統一して記載を行います。この異なる介入の値ごとの潜在アウトカムの比較によって因果関係を考えるというのが、Rubin流の因果推論の基本的な考え方になります。
※2 次回のコラム参照
※3 ある介入を受ける場合に各個人が潜在的に持っているアウトカムである点を強調するために潜在アウトカムと呼ぶとする主張と、必ずどれか1つの値しか得ることができず(事実)他の値は現実には得られない(反事実)ため反事実アウトカムと呼ぶとする主張がある
数学的な因果効果の記載
次にこの潜在アウトカムを用いた因果関係をを数学的に定義するために、まず以下のように記号の定義を行います※4。なおこのコラム・シリーズでは、アルファベットの大文字は確率変数、小文字はそれぞれの実現値を意味するものであるとします。
- i:個人を示すインデックス
- A:二値の介入を示す変数 (0: untreated,1: treated)
- Y:観測されたアウトカム (0: survive,1: death)
- Ya=0 :治療を受けない場合の潜在アウトカム
→(ゼウス:Ya=0 =0、ヘラ:Ya=0 =0 ) - Ya=1 :治療を受ける場合の潜在アウトカム
→(ゼウス: Ya=1 =1 、ヘラ:Ya=1 =0 )
ここである個人iに対して因果効果があるとは、Yia=0 ≠ Yia=1 である場合を意味します※5。 また実際には、因果効果があるかないかだけではなくその効果の大きさも興味の対象である場合がほとんどです。その因果効果の値を示す指標 (effect measures) としては、スケールごとにいくつか考えられますが、最もよく用いられるものの1つが介入を行った場合と行わなかった場合の差分を取ったものです。このとき、個人の因果効果 (individual causal effect) は
Yia=1 - Yia=0
として定義されます。
例えば心臓移植と5日後の生存に関する今回の具体例では、介入と潜在アウトカムに関して、下表のように4つのパターンが考えられます。「介入の因果効果がない」とは潜在アウトカムの差分 (causal effect) の値が0である場合であり、反対に「介入の因果効果がある」のは、その値が-1もしくは1である場合です。アウトカムYについては介入から5日後に死亡している場合に1と観測されますので、-1は介入により死亡が防がれたというpositiveな効果、1は介入により死亡が引き起こされたというnegativeな効果を意味しています。

またここまでは個人に対する因果効果を考えていましたが、集団に対する因果効果も同様に考えることが可能です。すなわち、介入を行う場合 (A=1) と行わない場合 (A=0) の、ある集団における潜在アウトカムの平均的な値について差があるかどうかを示すものであり、 具体的にはeffect measureを差分のスケールとして考えた場合には平均因果効果 (average causal effect) は
E[Yia=1 - Yia=0]
と定義されます。なお平均因果効果はアウトカムが二値である場合には、
E[Yia=1 - Yia=0] = Pr[Yia=1] - Pr[Yia=0]
となります。
ここでE[Yia=1]は集団全員が介入を受ける場合、E[Yia=0]は集団全員が受けない場合の潜在アウトカムの期待値です。平均因果効果は平均処置効果 (ATE; Average Treatment Effect) とも呼ばれ、医学関係者の方であれば耳にすることも多いかと思います。この平均因果効果について仮説検定を行うことが時にはありますが、その際に帰無仮説としては次の2つが考えられます。
- Fisher帰無仮説 (sharp null hypothesis)
すべての個人iに対して、Yia=1 - Yia=0 = 0
- Neyman帰無仮説
E[Yia=1 - Yia=0] = 0
Fisher帰無仮説は集団に含まれるすべての個人に対して因果効果がないことを、 Neyman帰無仮説は期待値に差がないことを意味するものであり、前者の方がより強い内容を意味していることに注意が必要です。つまり、すべての個人に対して因果効果がないのであれば(Fisher帰無仮説が真)、集団全体の因果効果がない(Neyman帰無仮説が真)ことは満たされるものの、その逆(すべての個人で因果効果がないこと)は成り立たちません。先程の表において、それぞれのパターンを被験者であるとみなし、4人の集団を表しているものとして再度考えてみます。すると平均因果効果は0+1+(-1)+0=0となり、Neyman帰無仮説が成立している状況(平均的には因果効果はない)となっています。しかし各個人について見てみると、因果効果がある人もない人もいるため、Fisher帰無仮説は成り立っていません。
※4 ここではゼウスとヘラの例に合わせて介入A、アウトカムYを共に二値変数としていますが、一般にはこれらは二値である必要はなく、多値もしくは連続値をとりうる場合でも同様に定義することが可能
※5 個人を示すiについては場合に応じて省略される
おわりに
今回のコラムでは、因果関係を潜在アウトカムという枠組みの中で定義しました。しかし多くの読者の方が察していますように、現実には潜在アウトカムの値を全て観察することはできません。よって一般には個人の因果効果に関しては定義することはできても、その値を求めることはできません。しかし、集団における平均因果効果については識別条件 (identifiability assumptions) と呼ばれる一連の仮定が成り立つのであれば、推定(識別)することが可能となります。次回のコラムでは、主にこの識別条件について、その内容と意図するところを紹介していきます。
補足
参考文献
- 岩崎学. (2015). 統計的因果推論, 朝倉書店
- Pearl, J., Glymour, M., and Jewell, N. P. (2019). 入門統計的因果推論. (落海浩訳). 朝倉書店
- Hernán, M. A. and Robins, J. M. (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC.
- 田中司朗. (2019). 医学のための因果推論の基礎概念,計量生物学 40(1), 35-62
- Imbens, G. W. and Rubin, D. B. (2015). Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction. Cambridge University Press.