この記事はSAS Institute Japanが翻訳および編集したもので、もともとはHui Liによって執筆されました。元記事はこちらです(英語)。
この記事では、関心対象の課題に適した機械学習アルゴリズムを特定・適用する方法を知りたいと考えている初級~中級レベルのデータ・サイエンティストや分析担当者を主な対象者としたガイド資料を紹介し、関連の基本知識をまとめます。
幅広い機械学習アルゴリズムに直面した初心者が問いかける典型的な疑問は、「どのアルゴリズムを使えばよいのか?」です。この疑問への答えは、以下を含む数多くの要因に左右されます。
- データの規模、品質、性質
- 利用できる計算時間
- タスクの緊急性
- データの利用目的(そのデータで何をしたいのか?)
経験豊富なデータ・サイエンティストでも、どのアルゴリズムが最も優れたパフォーマンスを示すかは、複数の異なるアルゴリズムを試してみなければ判断できません。本稿の目的は、特定の状況にのみ有効なアプローチを紹介することではなく、「最初に試すべきアルゴリズム」を何らかの明確な要因にもとづいて判断する方法についてガイダンスを示すことです。
機械学習アルゴリズム選択チートシート
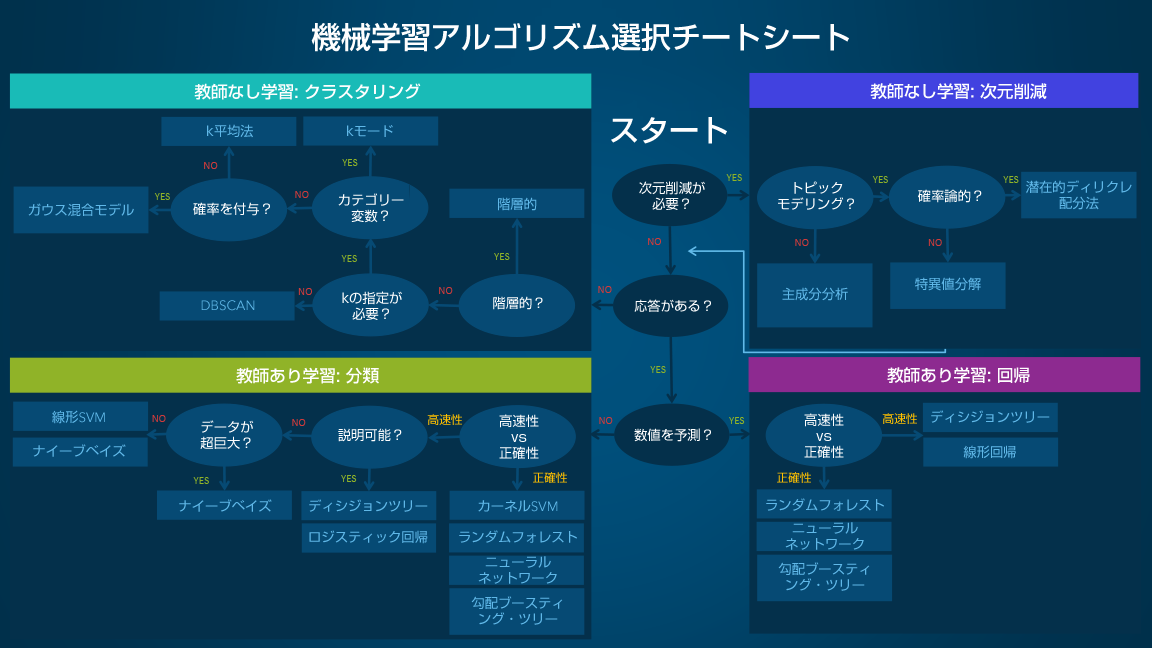
この機械学習アルゴリズム選択チートシートは、幅広い機械学習アルゴリズムの中から特定の課題に最適なアルゴリズムを見つけ出すために役立ちます。以下では、このシートの使い方と主要な基礎知識をひと通り説明します。
なお、このチートシートは初心者レベルのデータ・サイエンティストや分析担当者を対象としているため、推奨されるアルゴリズムの妥当性に関する議論は省いてあります。
このシートで推奨されているアルゴリズムは、複数のデータ・サイエンティストと機械学習の専門家・開発者から得られたフィードバックやヒントを取りまとめた結果です。推奨アルゴリズムについて合意に至っていない事項もいくつか残っており、そうした事項については、共通認識に光を当てながら相違点のすり合わせを図っているところです。
利用可能な手法をより包括的に網羅できるように、手元のライブラリが拡充され次第、新たなアルゴリズムを追加していく予定です。
チートシートの使い方
このシートは一般的なフローチャートであり、パス(楕円形)とアルゴリズム(長方形)が配置されています。各パスでYES/NO、または高速性/正確性を選びながら最終的に到達したものが推奨アルゴリズムとなります。いくつか例を挙げましょう。
- 次元削減を実行したいものの、トピック・モデリングを行う必要がない場合は、主成分分析を使うことになります。
- 次元削減が不要で、応答があり、数値を予測する場合で、高速性を重視するときには、デシジョン・ツリー(決定木)または線形回帰を使います。
- 次元削減が不要で、応答がない場合で、階層構造の結果が必要なときには、階層的クラスタリングを使います。
場合によっては、複数の分岐に当てはまることもあれば、どの分岐にも完璧には当てはまらないこともあるでしょう。なお、利用上の重要な注意点として、このシートは、あくまでも基本的な推奨アルゴリズムに到達できることを意図しているため、推奨されたアルゴリズムが必ずしも最適なアルゴリズムでない場合もあります。多くのデータ・サイエンティストが、「最適なアルゴリズムを見つける最も確実な方法は、候補のアルゴリズムを全て試してみることだ」と指摘しています。
機械学習アルゴリズムのタイプ
このセクションでは、機械学習の最も一般的なタイプを取り上げ、概要を示します。これらのカテゴリーについて十分な知識があり、具体的なアルゴリズムの話題に進みたい場合は、このセクションを飛ばし、2つ先のセクション「各種アルゴリズムの概要と用途」に進んでいただいてかまいません。
教師あり学習
教師あり学習アルゴリズムは、実例のセット(入力データと出力結果)を基に予測を行います。例えば、過去の販売データを用いて将来の価格を推定することができます。教師あり学習では、ラベル付きのトレーニング用データからなる入力変数と、それに対応する望ましい出力変数があります。アルゴリズムはトレーニング用データを分析し、入力を出力にマッピングする関数を学習します。この関数は、トレーニング用データにおける入力/出力の関係を一般化することによって推定されます。この関数に新しい未知の入力データを与えると、それに対応する出力が算出され、その出力が未知の状況における結果の予測値となります。
- 分類:データを用いてカテゴリー変数を予測する場合、教師あり学習は「分類」と呼ばれます。これは例えば、画像にラベルや標識(例:犬または猫)を割り当てるようなケースです。ラベルが2つしかない場合は「2値(バイナリ)分類」、3つ以上のラベルがある場合は「マルチクラス分類」と呼ばれます。
- 回帰:連続値を予測する場合、その教師あり学習は「回帰問題」となります。
- 予測:過去と現在のデータを基に将来を予測するプロセスであり、最も一般的な用途は傾向分析です。具体例として一般的なのは、当年度および過去数年の販売実績を基に次年度の販売額を推定することです。
半教師あり学習
教師あり学習を行う上での課題は、ラベル付きデータの準備に多大な費用と時間がかかりかねないことです。ラベル付きデータが限られている場合には、ラベルなしの実例データを用いて教師あり学習を強化することができます。これを行う場合は、機械にとって完全な「教師あり」ではなくなるため、「半教師あり」と呼ばれます。半教師あり学習では、ラベルなしの実例データと少量のラベル付きデータを使用することで、学習精度の向上を図ります。
教師なし学習
教師なし学習を実行する場合、機械にはラベルなしのデータのみが与えられます。学習の目的は、クラスタリング構造、低次元の多様体、スパース(疎)ツリーおよびグラフなど、データの基底をなす固有パターンを発見することです。
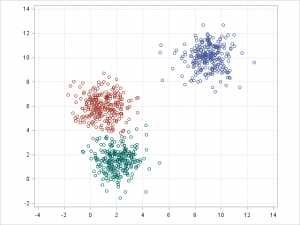
- クラスタリング:あるグループ(=クラスター)内の実例データ群が、その他のグループ内の実例データ群との間と比べ、(所定の基準に関して)高い類似性を示すような形で、実例データセットをグループ化します。この手法は、データセット全体を複数のグループにセグメント化する目的でよく使われます。グラスタリングの実行後に各グループ内で分析を実行すると、固有パターンを容易に発見できることが多々あります。
- 次元削減:検討の対象とする変数の数を減らします。多くの用途では、生データに極めて多次元の特徴が含まれており、一部の特徴は目的のタスクに対して冗長または無関係です。次元削減は、データに潜む真の関係性を発見するために役立ちます。
強化学習
強化学習は、環境からのフィードバックを基に「エージェント」(課題解決の主体者。例:ゲームのプレイヤー)の行動を分析および最適化します。機械は、取るべきアクションの選択肢を事前に教えられるのではなく、どのようなアクションが最大の報酬(例:ゲームのスコア)を生み出すかを発見するために、さまざまなシナリオを試行します。他の手法には見られない強化学習ならではの特徴は「試行錯誤」と「遅延報酬」です。
アルゴリズム選択時の考慮事項
アルゴリズムを選択する際は、正確性、トレーニング時間、使いやすさという3つの側面を常に考慮する必要があります。多くのユーザーは正確性を第一に考えますが、初心者は自分が最もよく知っているアルゴリズムに意識が向きがちです。
データセットが与えられたとき最初に考える必要があるのは、どのような結果になるにせよ、何らかの結果を得る方法です。初心者は、導入しやすく結果が素早く得られるアルゴリズムを選ぶ傾向がありますが、分析プロセスの最初の段階ではそれで問題ありません。まずは、何らかの結果を得て、データの概要を把握することを優先します。その後、データに対する理解を深め、結果をさらに改善することを目指し、より高度なアルゴリズムを試すことに時間を費やせばよいのです。
ただしこの段階でも、最高の正確性を示した手法が必ずしもその課題に最適なアルゴリズムであるとは限りません。通常、アルゴリズムから本来の最高パフォーマンスを引き出すためには、慎重なチューニングと広範囲のトレーニングが必要になるからです。
各種アルゴリズムの概要と用途
個別のアルゴリズムについて知識を深めることは、得られる結果と使い方を理解するために役立ちます。以下では、チートシートに掲載されている中でも最も基本的なアルゴリズムの詳細と、それらを使用すべき状況に関するヒントをまとめます。
線形回帰とロジスティック回帰
- 線形回帰
- ロジスティック回帰
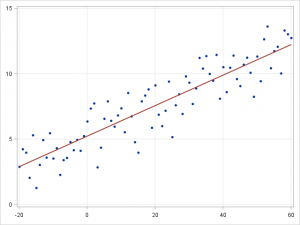
線形回帰は、連続従属変数 \(y\) と1つ以上の予測変数 \(X\) との関係をモデリングするためのアプローチです。この場合、\(y\) と \(X\) の関係は、\(y=\beta^TX+\epsilon\) として線形でモデル化できます。トレーニング用の実例 \(\{x_i,y_i\}_{i=1}^N\) が与えられると、パラメータ・ベクトル \(\beta\) を学習することができます。
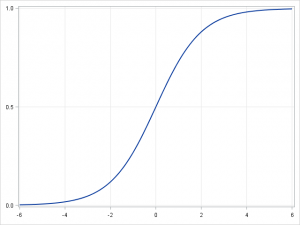
従属変数が連続変数ではなくカテゴリー変数の場合には、線形回帰を、logitリンク関数を用いてロジスティック回帰に変換することができます。ロジスティック回帰は、シンプルかつ高速ながらパワフルな分類アルゴリズムです。ここでは、従属変数 \(y\) が \(\{y_i\in(-1,1)\}_{i=1}^N\) という2つの値のみを取る、2値(バイナリ)のケースについて説明します(これはマルチクラス分類問題に容易に拡張可能です)。
ロジスティック回帰では、与えられた実例がクラス「1」に属する確率とクラス「-1」に属する確率の予測を試みるために、複数の異なる仮説クラスを使用します。具体的には、\(p(y_i=1|x_i )=\sigma(\beta^T x_i )\) および \(p(y_i=-1|x_i )=1-\sigma(\beta^T x_i )\) という形の関数の学習を試みます。ここで、\(\sigma(x)=\frac{1}{1+exp(-x)}\) シグモイド関数です。トレーニング用の実例 \(\{x_i,y_i\}_{i=1}^N\) が与えられると、与えられたデータセットで \(\beta\) の対数尤度を最大化することにより、パラメータ・ベクトル \(\beta\) を学習することができます。
- グループ別の線形回帰
- ロジスティック回帰
線形SVMとカーネルSVM
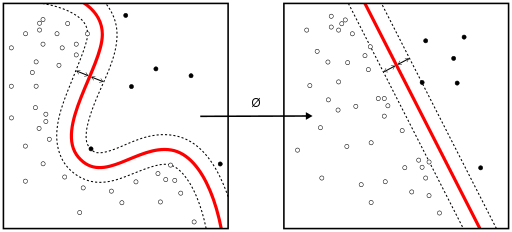
非線形分離可能な関数を、より高次元の線形分離可能な関数にマッピングするために用いられる手法を「カーネルトリック」と呼びます。サポート・ベクター・マシン(SVM)のトレーニング・アルゴリズムは、超平面の法線ベクトル \(w\) とバイアス \(b\) で表現される分類子を発見します。この超平面(境界)は、可能な限り幅の広いマージンによって、異なるクラスを分離します。この問題は、条件付き最適化問題に変換可能です。
\begin{equation*}
\begin{aligned}
& \underset{w}{\text{minimize}}
& & ||w|| \\
& \text{subject to}
& & y_i(w^T X_i-b) \geq 1, \; i = 1, \ldots, n.
\end{aligned}
\end{equation*}
クラスが線形分離可能ではない場合は、カーネルトリックを利用することで、非線形分離可能な空間を、より高次元の線形分離可能な空間にマッピングすることができます。
ほとんどの従属変数が数値の場合には、最初に試してみる分類アルゴリズムとして、ロジスティック回帰とSVMを選ぶのが妥当です。これらのモデルは導入しやすく、パラメータのチューニングが容易で、パフォーマンスもかなり優れているため、初心者に適したモデルと言えます。
デシジョン・ツリー(決定木)とアンサンブル・ツリー
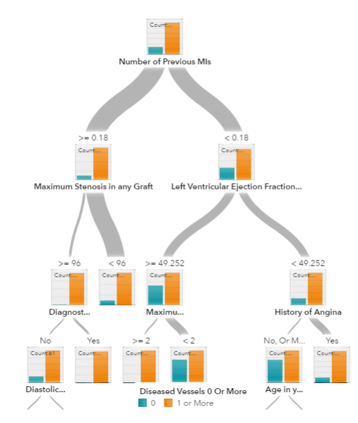
デシジョン・ツリー、ランダムフォレスト、勾配ブースティングは全て、デシジョン・ツリーにもとづくアルゴリズムです。デシジョン・ツリーには多くの変種がありますが、アルゴリズムとしての基本動作は全て同じであり、特徴空間を「ほぼ同じラベルを持つ部分領域」群に分割します。デシジョン・ツリーは理解や実装が容易ですが、ブランチ(枝)を使い尽くしてしまうと過学習(過剰な当てはめ、過剰適合)になり、ツリーが深くなりすぎる傾向があります。ランダムフォレストと勾配ブースティングは、十分な正確性を達成しながら過学習の問題も克服するためにツリー・アルゴリズムを利用する手法であり、この目的で広く使われている2大手法です。
ニューラル・ネットワークとディープ・ラーニング
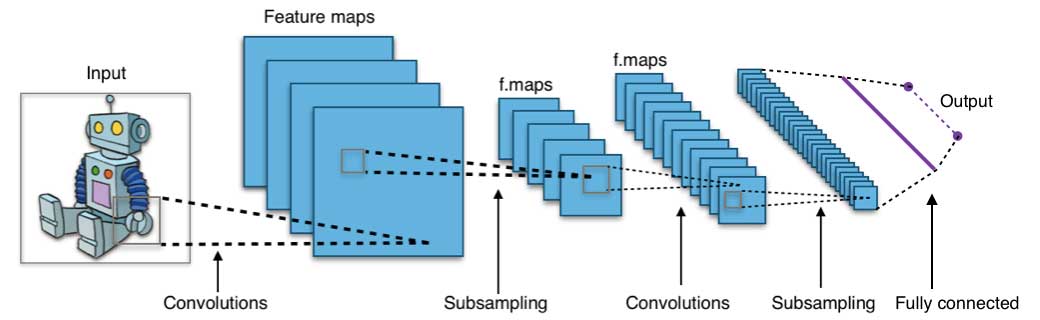
ニューラル・ネットワークは、並列および分散処理能力への期待から、1980年代中期に活発に研究されました。しかし、ニューラル・ネットワークのパラメータを最適化するために広く用いられる誤差逆伝搬法のトレーニング・アルゴリズムは効率が悪く、それがこの領域の研究の足かせとなりました。その後は、サポート・ベクター・マシン(SVM)やその他のより単純なモデルが、凸最小化問題の解決を通じて容易にトレーニング可能であることから、機械学習の領域では徐々にニューラル・ネットワークの代わりに使われるようになっていきました。
近年になると、教師なし事前学習や層ごとの貪欲法学習などの改善された新しい学習手法の登場により、ニューラル・ネットワークが改めて大きな関心を集めるようになりました。また、GPU(Graphical Processing Unit)やMPP(超並列処理)など、強力なコンピューティング機能が順調に発展していることも、ニューラル・ネットワーク導入熱の再燃に拍車をかけています。ニューラル・ネットワークの研究が再活性化したことで、今では、数千個の層からなるモデルも生み出されています。
言い換えると、浅いニューラル・ネットワークがディープ・ラーニング型のニューラル・ネットワークへと進化を遂げた、ということです。実際、ディープ・ニューラル・ネットワークは、教師あり学習に関して大きな成功を収めています。音声認識や画像認識に使用すると、ディープ・ラーニングは人間と同等か、場合によっては人間を凌ぐパフォーマンスを発揮します。また、ディープ・ラーニングを特徴抽出などの教師なし学習のタスクに適用すると、人間がほとんど介入しなくても、生の画像や音声から特徴を抽出することができます。
ニューラル・ネットワークは、入力層、(複数の)隠れ層、出力層という3種類の要素で構成されます。トレーニング用サンプルにより、入力層と出力層が定義されます。出力層がカテゴリー変数の場合、ニューラル・ネットワークは分類問題を解決する方法となります。出力層が連続変数の場合は、回帰問題の解決にニューラル・ネットワークを利用できます。出力層が入力層と同じ場合には、固有の特徴を抽出するためにニューラル・ネットワークを利用できます。モデルの複雑さとモデリング・キャパシティは、隠れ層の数で決まります。
k平均法/kモード・クラスタリングとGMM(ガウス混合モデル)クラスタリング
- k平均法クラスタリング
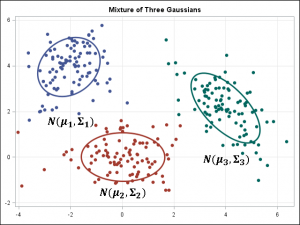
- ガウス混合モデル
k平均法/kモード・クラスタリングとGMMクラスタリングの目的は、n個のオブザベーションをk個のクラスターにパーティション化することです。k平均法はハード(厳密)な割り当てを定義し、サンプルはそれぞれ1つのクラスターにのみ関連付けられます。一方、GMMはソフト(緩やか)な割り当てを定義します。各サンプルには、個々のクラスターに関連付けられる確率が付与されます。どちらのアルゴリズムも仕組みは単純であり、クラスター数 k が与えられると十分な高速さでクラスタリングが実行されます。
DBSCAN(密度ベースの空間クラスタリング)
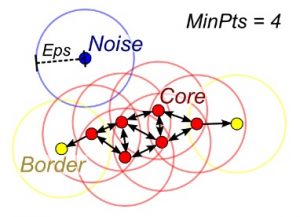
クラスター数 k が与えられない場合は、DBSCAN(密度ベースの空間クラスタリング)を使用できます。この手法では、密度拡散を通じてサンプルを結びつけます。
階層的クラスタリング
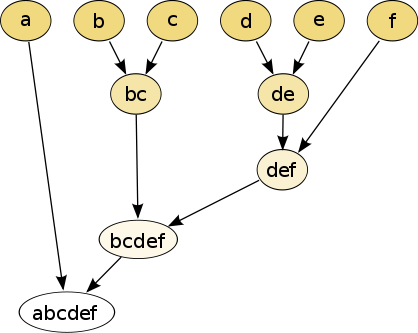
階層的なパーティションは、デンドログラム(=樹形図)と呼ばれるツリー構造を用いて視覚化することができます。この手法ではクラスター数を入力として与える必要がなく、パーティションは、異なる K を用いて異なるレベルの粒度で表示されます(つまり、クラスターの微細化や粗大化が可能です)。
PCA、SVD、LDA
一般に、多数の特徴を機械学習アルゴリズムに直接与えることは望ましくありません。なぜなら、問題とは無関係な特徴が含まれている可能性や、「固有の」次元数が特徴の数よりも少ない可能性があるからです。主成分分析(PCA)、特異値分解(SVD)、潜在的ディリクレ配分法(LDA)は全て、次元削減を行うために利用できます。
PCAは教師なしクラスタリング手法の一種であり、元のデータ空間をより低次元の空間にマッピングしながら、可能な限り多くの情報を保持します。PCAは基本的に、データ分散を最大限に保持するような部分空間を発見します。この部分空間は、データの共分散行列の主固有ベクトルによって定義されます。
SVDは、「中心化済みデータ行列(特徴とサンプルの行列)のSVDが、PCAで発見されるのと同じ部分空間を定義する優位な左特異ベクトルを提供する」という意味で、PCAと関連しています。しかしSVDは、より汎用性の高い手法であり、PCAに出来ないことも行えます。例えば、ユーザーと映画に関する行列のSVDを使用すると、ユーザーのプロファイルと映画のプロファイルを抽出し、レコメンデーション・システムで活用することができます。またSVDは、自然言語処理(NLP)において、潜在的意味解析と呼ばれるトピック・モデリング・ツールとしても広く利用されています。
潜在的ディリクレ配分法(LDA)も、NLPに関連した手法です。LDAは確率論的トピックモデルであり、GMM(ガウス混合モデル)が連続データをガウス密度に分解するのと同様の方法で、文書をトピックに分解します。LDAがGMMと異なる点は、離散データ(文書内の単語)をモデル化することと、トピックはディリクレ分布に従って ”アプリオリ” に分布されるという制約があることです。
まとめ
機械学習アルゴリズムの選択は、シンプルなワークフローに沿って進めることが可能です。新たな課題の解決を試みる際の主要ステップは、次のとおりです。
- 課題を定義します。機械学習で解決したい課題は何でしょうか?
- 最初は単純なアルゴリズムを試します。データと、基準となる結果について理解を深めます。
- その上で、より複雑なアルゴリズムを試します。
なお、オープンなAIプラットフォームSAS Viyaで機械学習を行う際に必要となる、具体的なプロシージャやメソッドの選択については、ぜひ「SAS Viyaのチートシートを作ってみました」もご一読ください。
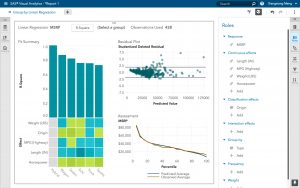
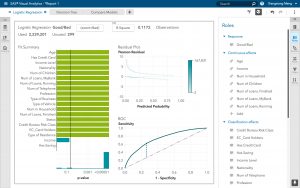
またSAS Viyaの製品であるSAS Visual Data Mining and Machine Learningは、初心者が機械学習について学び、課題への機械学習アルゴリズムの適用を試してみるためのプラットフォームとしても優れています。今すぐ無償試用版(英語)にご登録ください。