„Here comes Chicago. 17 seconds, 17 seconds from Game 7 or from Championship number 6. Jordan open. Chicago with the lead.“ Diese Worte eines Fernsehkommentators beschreiben den entscheidenden Wurf von Michael Jordan in Spiel 6 der NBA Finals 1997/98 zwischen den Chicago Bulls und den Utah Jazz, der wohl viele achtjährige Jungen davon träumen ließ, eines Tages die Meisterschaft für die Bulls zu entscheiden.

Auch wenn heute, bei einer Körpergröße von 1,80 m und der Spielweise von Dennis Rodman, der NBA-Traum für mich ausgeträumt ist, bleibt meine Faszination für einen Spieler, der unter Druck noch über sich hinauszuwachsen scheint. Meine Kollegen Thomas Bodenmüller-Dodek, Rick Wicklin und Robert Allison  haben gezeigt, wie sich die Wurfposition des Basketballers Steph Curry auf seine Treffsicherheit auswirkt. Lassen Sie uns am Beispiel von Michael Jordans Spielzeiten 1996/1997 und 1997/1998 einen weiteren Faktor hinzunehmen und analysieren, ob und wie Jordans Trefferquote durch Drucksituationen beeinflusst wird.

Jede Menge Daten zum Analysieren

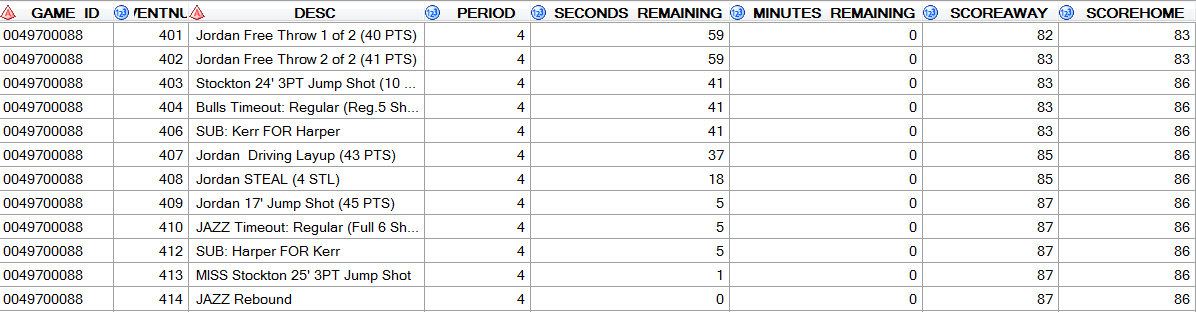
Die NBA stellt mit den „Shotchart-Details“ Wurfstatistiken einzelner Spieler inklusive Wurfposition auf dem Feld zur Verfügung. Neben den Shotchart-Details bietet die NBA auch Zugang zu den sogenannten „Play-by-Plays“ (Get Game), die detailliert einzelne Aktionen eines Spiels sowie den Spielstand in der jeweiligen Situation beschreiben. Durch Verbindung beider Datenquellen lassen sich zur Analyse von Jordans Treffsicherheit unter Druck einige Indikatoren ableiten – beispielsweise ob ein Spielergebnis knapp war (z.B. maximal fünf Punkte Rückstand oder Führung) oder ob sich ein Spiel dem Ende zuneigt(z.B. die letzten fünf Minuten des vierten Viertels oder Verlängerung). Als Drucksituationen definieren wir für die folgende Analyse die Endphase eines Spieles, wenn die Differenz zwischen beiden Teams weniger als 5 Punkte beträgt.

Abbildung 1: Letzte Minute der NBA Finals 1997/1998

Berechnung der Trefferquote unter Druck

Ziel der prädiktiven Modellierung ist es, ein Modell zu erstellen, das es ermöglicht, auf Basis von Input-Faktoren (z.B. Entfernung, Winkel, verbleibende Zeit, Spielstand) Werte einer Zielgröße oder Wahrscheinlichkeiten für Events (Jordan trifft vs. Jordan trifft nicht) akkurat zu prognostizieren.

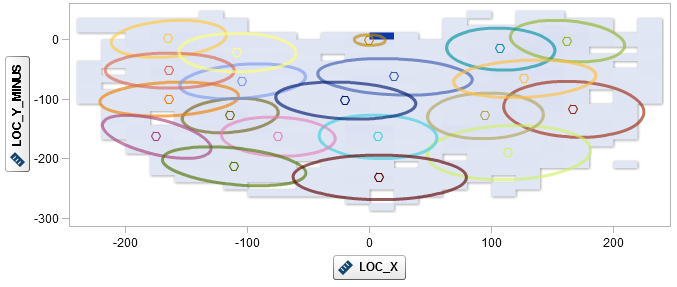
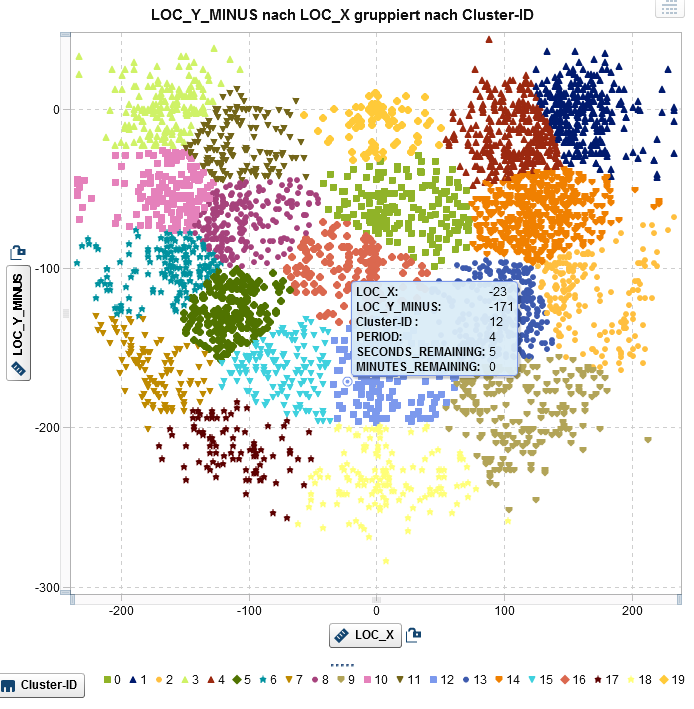
Die logistische Regression erlaubt die Schätzung des Einflusses von Drucksituationen auf die sogenannte log-odds ratio. So lässt sich nicht nur die Frage beantworten, ob Jordans Treffsicherheit sich unter Druck verändert, sondern auch, ob sie beispielsweise abhängig von der Position auf dem Spielfeld oder der Wurfart (z.B. Hook Shot vs. Jump Shot) variiert. Eine einfache Möglichkeit zur Berücksichtigung der Wurfposition ergibt sich mit der Unterteilung des Spielfelds in einzelne Segmente. Dazu wurde das Spielfeld mittels k-Means in 20 Cluster unterteilt. Ausreißer (Würfe mit einer Distanz größer als 30 ft.) wurden ausgeschlossen. Die einzelnen Segmente können als Inputfaktoren in das Modell integriert werden.

Abbildung 2: Jordans Wurfversuche der Saison 1996/1997 und 1997/1998

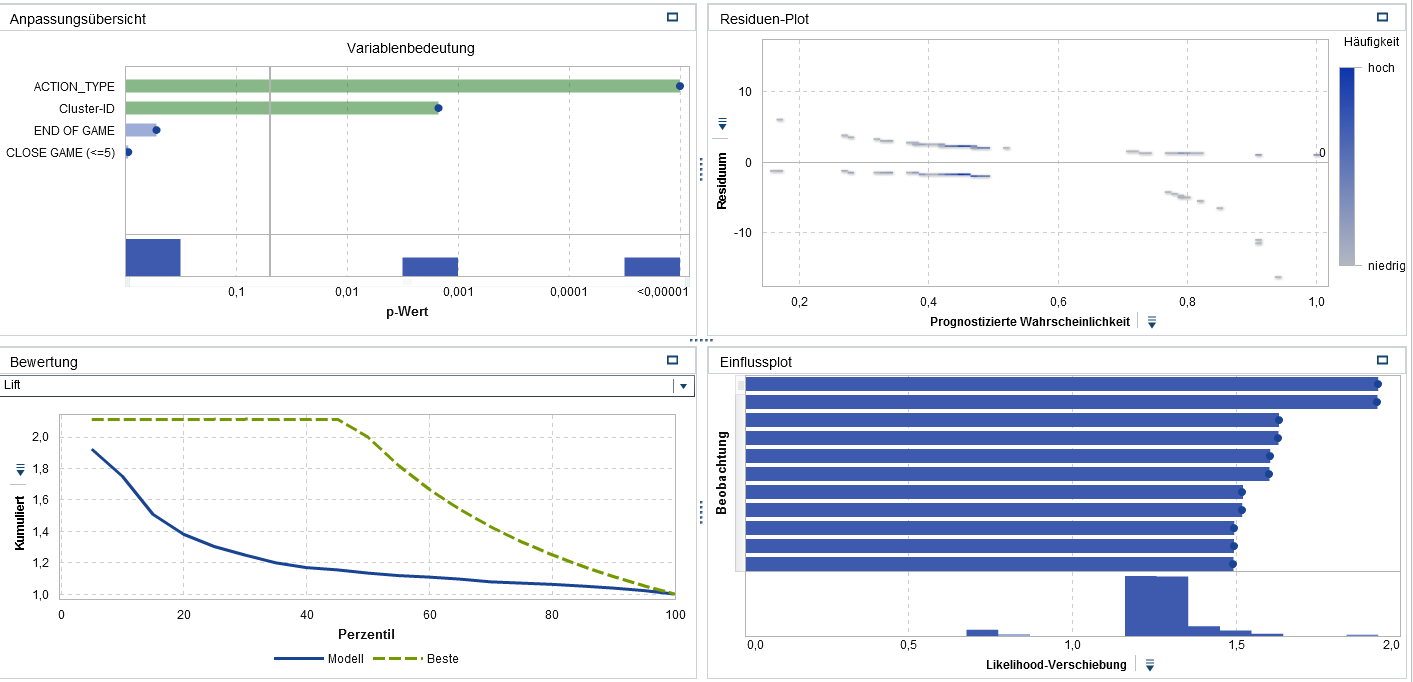
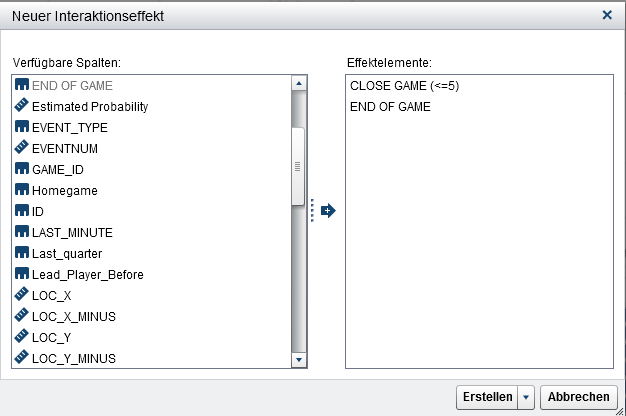
Das einfache logistische Regressionsmodell zeigt, dass die Art des Wurfes und die Position auf dem Spielfeld signifikante Einflussfaktoren für Jordans Treffsicherheit sind. Die Treffsicherheit variiert dagegen nicht gegen Ende des Spiels oder bei nah beieinander liegenden Spielständen. Um die Frage zu beantworten, ob und wie sich Druck auf Jordans Trefferquote auswirkt, kann ein Interaktionsterm zwischen dem „knappen Spiel“ und den letzten Minuten eines Spiels abgeleitet werden.

 

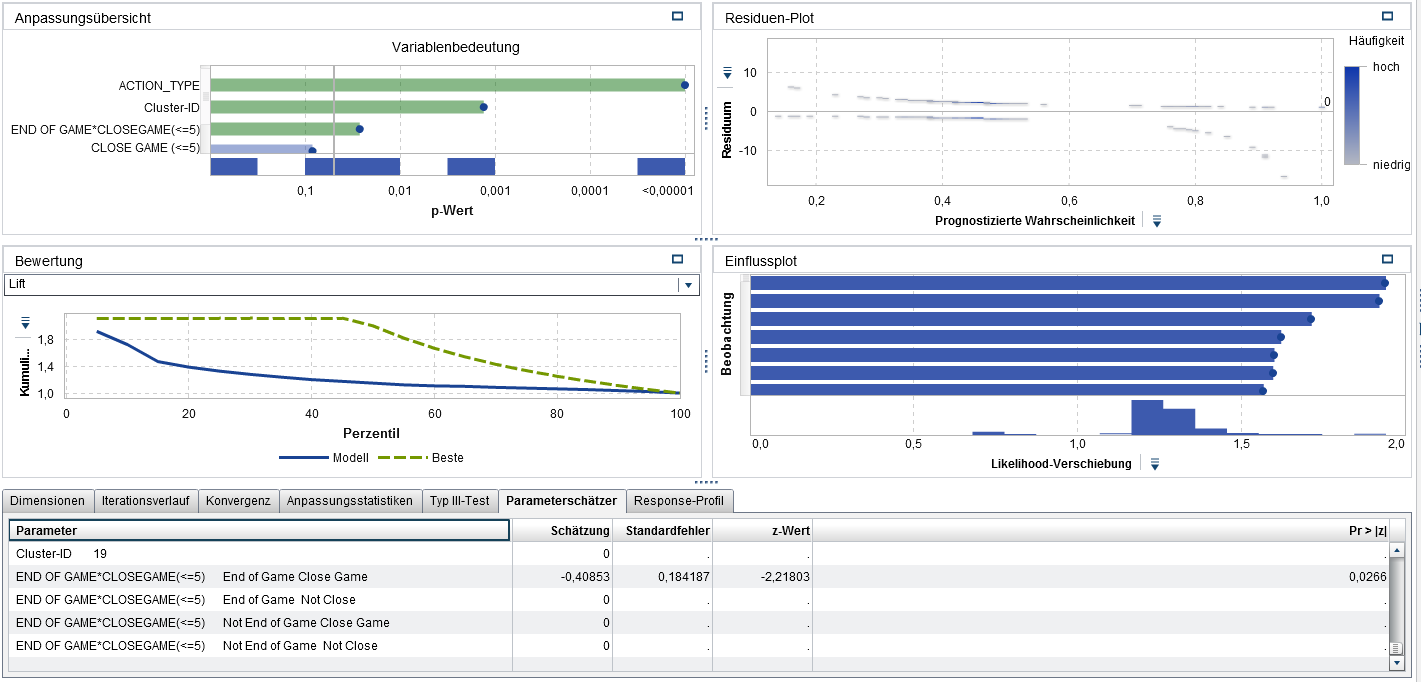
Welchen Einfluss hat nun Druck auf Jordans Performance? Der Parameterschätzer beträgt -0,41 und ist signifikant von null verschoben. Betrachten wir Wurfposition und Wurfart, deutet unser Modell auf eine sinkende Trefferquote Jordans gegen Ende des Spiels hin, wenn der Spielstand eng ist. Wie lässt sich daraufhin die Stärke dieses Effektes interpretieren? Bei der logistischen Regression hängt der Effekt auf die Trefferwahrscheinlichkeit vom Level der Inputfaktoren ab. Lassen Sie uns den „Last Shot“ als Beispiel nehmen. Unser Modell prognostiziert eine Wahrscheinlichkeit von ca. 36 Prozent, dass der Ball im Korb landet. Ein Wurf unter den gleichen Umständen (Jump Shot in Spielfeldsegment 12 gegen Ende des Spiels) bei einem Abstand von mehr als 5 Punkten bekommt dagegen eine Wahrscheinlichkeit von 45 Prozent zugewiesen.

Wie robust ist das Modell? Eine Modellierung durch ein Generales Additives Modell mit SAS/STAT unter Verwendung der PROC GAMPL liefert ähnliche Resultate. Weitere Robustheitstests erfordern natürlich zusätzlich verschiedene Definitionen von Druck.

Nicht die ganze Wahrheit

Lässt sich aus den Ergebnissen schließen, dass man Jordan in der „Crunch Time“ nicht den Ball geben sollte? Nein. Zum einen sind potenziell wichtige Erklärungsfaktoren nicht in das Modell integriert. Beispielsweise könnten gegnerische Teams Jordan in wichtigen Situationen „gedoublet“ (mit zwei Spielern verteidigt) haben, was zu einer geringeren Trefferquote führen kann. Unabhängig davon ist letztendlich nicht entscheidend, ob Jordan unter Druck besser oder schlechter traf, sondern ob er die beste Option für den entscheidenden Wurf war. Wie treffsicher Jordans Team-Kollegen Harper, Pippen, Rodman und Kerr unter Druck agieren, bliebe schließlich noch zu analysieren.

Jordan bringt es selbst auf den Punkt: „I’ve missed more than 9,000 shots in my career. I’ve lost almost 300 games. 26 times, I’ve been trusted to take the game winning shot and missed. I’ve failed over and over in my life and that is why I succeeded.“