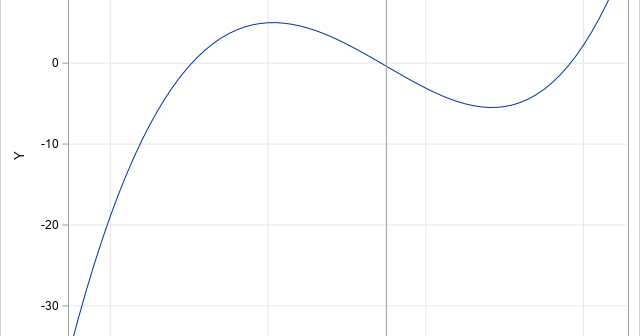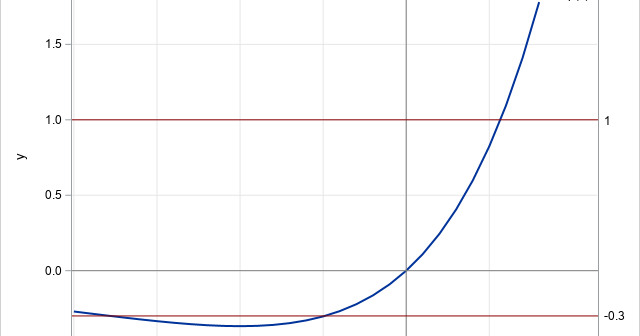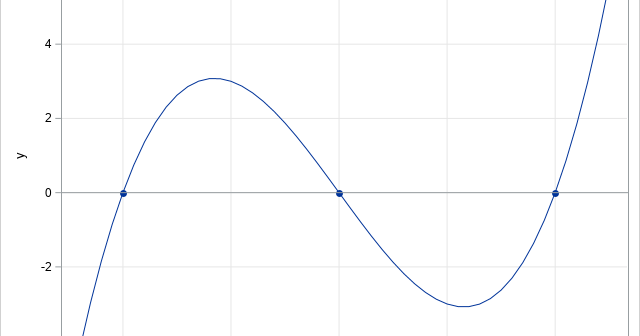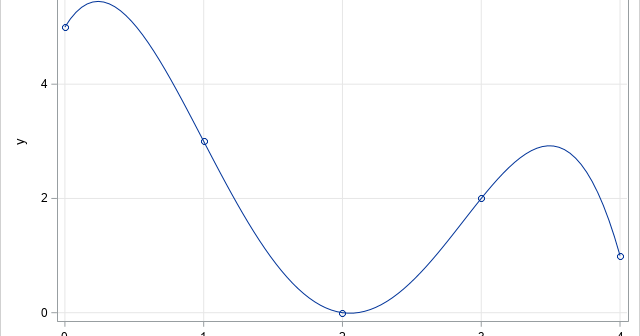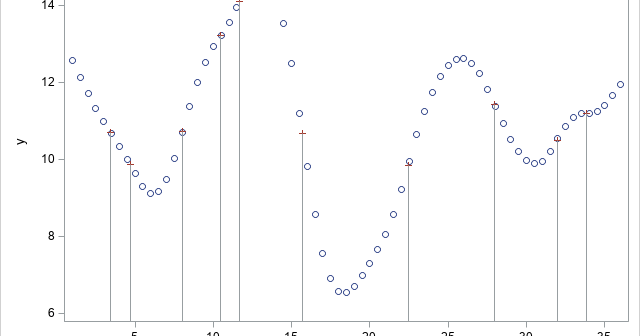
A previous article describes how to use SAS to find the inflection points of a 1-D function that you can evaluate at any point. The function must be given by a formula (or by an algorithm) because the root-finding algorithm needs to evaluate the function at arbitrary locations. However, sometimes