A SAS programmer asked if it is possible to numerically find an inflection point for a univariate function, f(x). Yes! This can be solved as a variation of a classic numerical root-finding problem.

Recall that an inflection point is a value (call it x0) in the domain where the graph of the function changes from concave up to concave down, or vice versa. In other words, the second derivative of the function is negative on one side of x0 and positive on the other side of x0. Generically, for a function that has a continuous second derivative, the second derivative of the function must pass through zero at x0. Thus, you can find the inflection points of f(x) by finding the roots of f''(x), which is the second derivative function.

In a calculus class, this problem is solved analytically: You find the second derivative of the function, f''(x), then solve the equation f''(x)=0 for values of x. The solutions are potential inflection points. Unfortunately, solving for roots analytically is usually impossible unless f is a very simple function such as a low-order polynomial or a trig function. Thus, in practice, you almost always need to use numerical root-finding methods. In SAS, you can use the FROOT function in PROC IML to find the roots of a differentiable 1-D function on a specified interval.

Roots of exact second derivatives

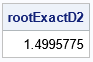
For a simple function, you can use calculus to derive the formula for the second derivative of the function. Then the problem is straightforward to solve numerically: You create a user-defined function that evaluates the second derivative and call the FROOT function to find locations where the second derivative is zero. This is shown in the following SAS IML program, which defines two functions. The FUNC function evaluates the function for which we wish to find the point(s) of inflection. It is the sum of a trigonometric function and a polynomial. The EXACTD2 function is the exact second derivative. The call to the FROOT function finds a root (zero) of the second derivative function in the interval. The root is found at approximately x = 1.5.

proc iml;
start Func(x);
   return sin(x) + x##3 - 4*x##2 - 0.5*x + 5;
finish;
 
/* f'(x)  =  cos(x) + 3*x##2 - 8*x - 0.5
   f''(x) = -sin(x) + 6*x    - 8 */
start ExactD2(x);
   return -sin(x) + 6*x - 8;
finish;
 
rootExactD2 = froot("ExactD2", {-2.5, 3.5});
print rootExactD2;

To ensure that the point is truly an inflection point, you can graph the function and add a reference line at the value. The following graph shows that this function is concave down to the left of the inflection point and concave up to the right:

x = T(do(-2.5, 4.5, 0.1));
y = Func(x);
reflineStmt = "refline " + char(rootExactD2) + "/ axis=x;";
title "Function and Inflection Point";
call series(x, y) grid={x y} other=reflineStmt;

Roots of finite-difference second derivatives

For various reasons, you might prefer to to ask SAS for a numerical approximation of the second derivative function. No problem! In SAS IML you can use the NLPFDD function to obtain numerical second derivatives from the function itself. Or, in SAS Viya, you can use the newer FDDSOLVE function to approximate the second derivative of a function.

To obtain the finite-difference second derivative, you can write a function that calls the NLPFDD function and returns only the second derivative information. It can be useful to write functions so that they accept a vector of x values. (This was done for the EXACTD2 function in the previous section.) For finite-difference derivatives, you must write a loop that iterates over the x values, as follows:

/* use finite-difference methods to estimate second derivative of a
   scalar function of one variable, "Func", at a vector of x values.
   https://blogs.sas.com/content/iml/2022/03/02/finite-difference-derivatives-sas.html
*/
start FDD2(x);
   parm = {.,  01, .};                /* central diff based on objective function */
   fdd = j(nrow(x), ncol(x), .);
   do i = 1 to nrow(x)*ncol(x);
      call nlpfdd(f, D1, D2, "Func", x[i], parm);
      fdd[i] = D2;
   end;
   return fdd;
finish;
 
/* call the function and graph it */ 
x = T(do(-2.5, 4.5, 0.1));
FDD2 = FDD2(x);
title "Finite-Difference Second Derivative of Function";
call series(x, FDD2) grid={x y} other="refline 0; xaxis grid values=(-2.5 to 4.5 by 0.5);";

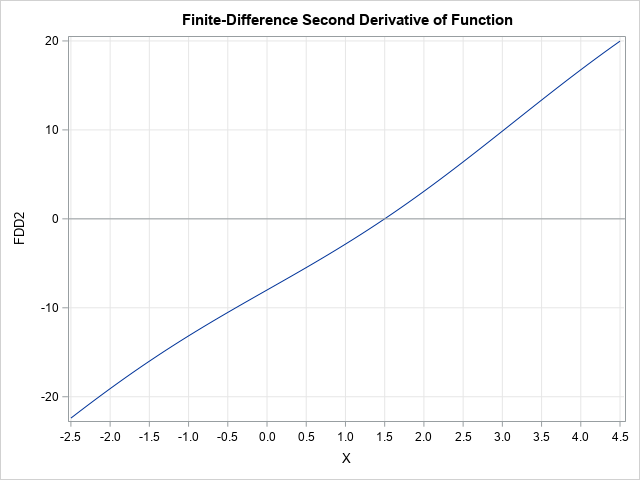
This graph of the second derivative shows that the second derivative is negative to the left of the root and positive to the right of the root.

To obtain a numerical root from the finite-difference second derivative, simply call the FROOT function and tell it to find a root of the FDD2 function, as follows:

rootD2 = froot("FDD2", {-2.5, 4.5});
print rootExactD2 rootD2;

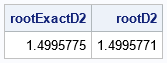
For comparison, the root of the exact second derivative function is shown next to the root of the finite-difference approximation. The two roots agree to six decimal places.

Summary

If you have a formula for a smooth function, you can find the inflection points for the function by finding the (transverse) roots of the second derivative of the function. In many situations, you can write a formula for the second derivative. However, if the function is given by a algorithm or the second derivative is too complicated to write down, you can use finite-difference derivatives to approximate the second derivative. You can use the FROOT function in SAS IML to find a root of this approximation. The root is a point at which the original function changes concavity from convex up to convex down, or vice versa.