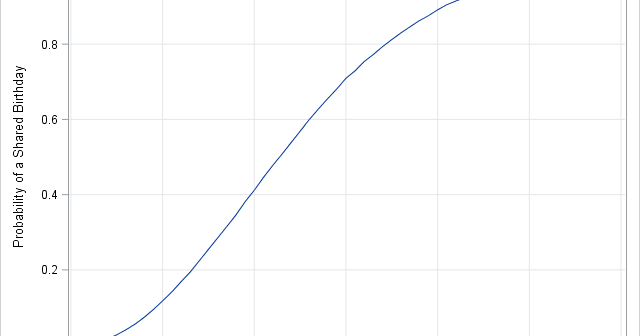
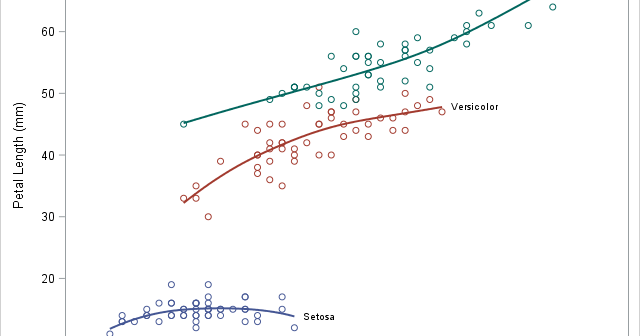
If N random people are in a room, the classical birthday problem provides the probability that at least two people share a birthday. The birthday problem does not consider how many birthdays are in common. However, a generalization (sometimes called the Multiple-Birthday Problem) examines the distribution of the number of