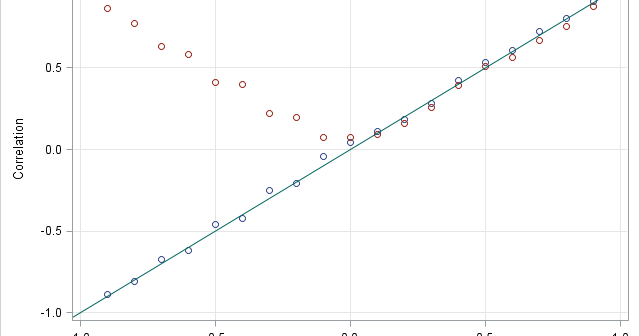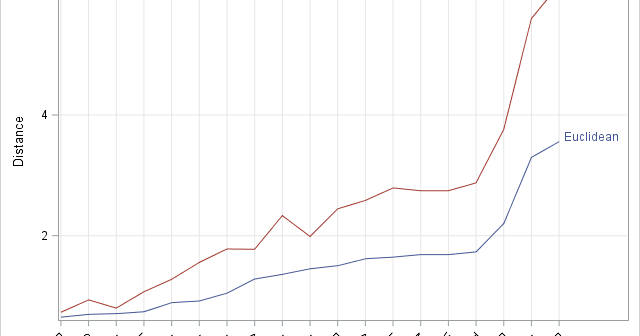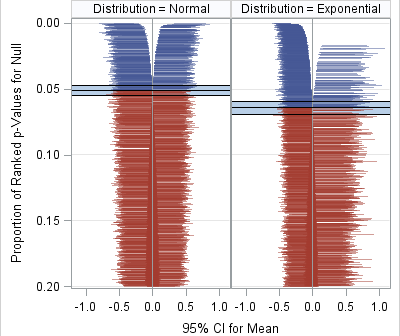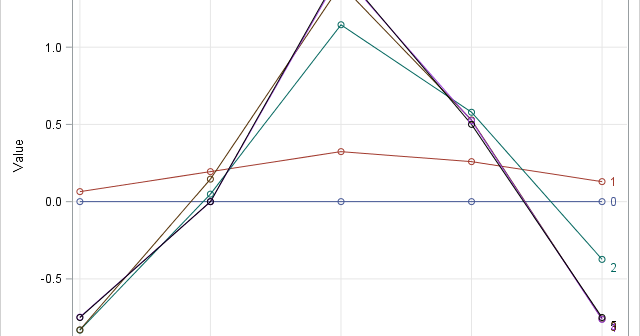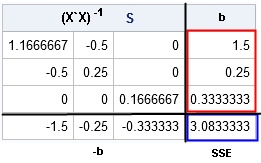
The sweep operator performs elementary row operations on a system of linear equations. The sweep operator enables you to build regression models by "sweeping in" or "sweeping out" particular rows of the X`X matrix. As you do so, the estimates for the regression coefficients, the error sum of squares, and