Last week Warren Kuhfeld wrote about a graph called the "lines plot" that is produced by SAS/STAT procedures in SAS 9.4M5. (Notice that the "lines plot" has an 's'; it is not a line plot!) The lines plot is produced as part of an analysis that performs multiple comparisons of means. Although the graphical version of the lines plot is new in SAS 9.4M5, the underlying analysis has been available in SAS for decades. If you have an earlier version of SAS, the analysis is presented as a table rather than as a graph.
Warren's focus was on the plot itself, with an emphasis on how to create it. However, the plot is also interesting for the statistical information it provides. This article discusses how to interpret the lines plot in a multiple comparisons of means analysis.
The lines plot in SAS
You can use the LINES option in the LSMEANS statement to request a lines plot in SAS 9.4M5. The following data are taken from Multiple Comparisons and Multiple Tests (p. 42-53 of the First Edition). Researchers are studying the effectiveness of five weight-loss diets, denoted by A, B, C, D, and E. Ten male subjects are randomly assigned to each method. After a fixed length of time, the weight loss of each subject is recorded, as follows:
/* Data and programs from _Multiple Comparisons and Multiple Tests_ Westfall, Tobias, Rom, Wolfinger, and Hochberg (1999, First Edition) */ data wloss; do diet = 'A','B','C','D','E'; do i = 1 to 10; input WeightLoss @@; output; end; end; datalines; 12.4 10.7 11.9 11.0 12.4 12.3 13.0 12.5 11.2 13.1 9.1 11.5 11.3 9.7 13.2 10.7 10.6 11.3 11.1 11.7 8.5 11.6 10.2 10.9 9.0 9.6 9.9 11.3 10.5 11.2 8.7 9.3 8.2 8.3 9.0 9.4 9.2 12.2 8.5 9.9 12.7 13.2 11.8 11.9 12.2 11.2 13.7 11.8 11.5 11.7 ; |
You can use PROC GLM to perform a balanced one-way analysis of variance and use the MEANS or LSMEANS statement to request pairwise comparisons of means among the five diet groups:
proc glm data=wloss; class diet; model WeightLoss = diet; *means diet / tukey LINES; lsmeans diet / pdiff=all adjust=tukey LINES; quit; |
In general, I use the LSMEANS statement rather than the MEANS statement because LS-means are more versatile and handle unbalanced data. (More about this in a later section.) The PDIFF=ALL option requests an analysis of all pairwise comparisons between the LS-means of weight loss for the different diets. The ADJUST=TUKEY option is a common way to adjust the widths of confidence intervals to accommodate the multiple comparisons. The analysis produces several graphs and tables, including the following lines plot.
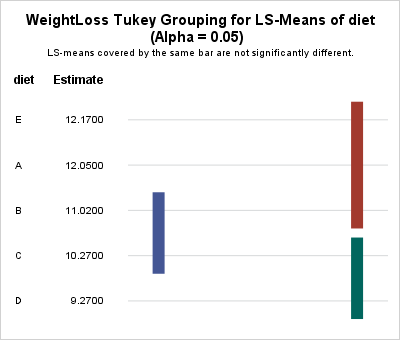
How to interpret a lines plot
In the lines plot, the vertical lines visually connect groups whose LS-means are "statistically indistinguishable." Statistically speaking, two means are "statistically indistinguishable" when their pairwise difference is not statistically significant.
If you have k groups, there are k(k-1)/2 pairwise differences that you can examine. The lines plot attempts to summarize those comparisons by connecting groups whose means are statistically indistinguishable. Often there are fewer lines than pairwise comparisons, so the lines plot displays a summary of which groups have similar means.
In the previous analysis, there are five groups, so there are 10 pairwise comparisons of means. The lines plot summarizes the results by using three vertical lines. The leftmost line (blue) indicates that the means of the 'B' and 'C' groups are statistically indistinguishable (they are not significantly different). Similarly, the upper right vertical bar (red) indicates that the means of the pairs ('E','A'), ('E','B'), and ('A','B') are not significantly different from each other. Lastly, the lower right vertical bar (green) indicates that the means for groups 'C' and 'D' are not significantly different. Thus in total, the lines plot indicates that five pairs of means are not significantly different.
The remaining pairs of mean differences (for example, 'E' and 'D') are significantly different. By using only three vertical lines, the lines plot visually associates pairs of means that are essentially the same. Those pairs that are not connected by a vertical line are significantly different.
Advantages and limitations of the lines plot
Advantages of the lines plot include the following:
- The groups are ordered according to the observed means of the groups.
- The number of vertical lines is often much smaller than the number of pairwise comparisons between groups.
Notice that the groups in this example are the same size (10 subjects). When the group sizes are equal (the so-called "balanced ANOVA" case), the lines plot can always correctly represent the relationships between the group means. However, that is not always true for unbalanced data. Westfall et al. (1999, p. 69) provide an example in which using the LINES option on the MEANS statement produces a misleading plot.
The situation is less severe when you use the LSMEANS statement, but for unbalanced data it is sometimes impossible for the lines plot to accurately connect all groups that have insignificant mean differences. In those cases, SAS appends a footnote to the plot that alerts you to the situation and lists the additional significances not represented by the plot.
In my next blog post, I will show some alternative graphical displays that are appropriate for multiple comparisons of means for unbalanced groups.
Summary
In summary, the new lines plot in SAS/STAT software is a graphical version of an analysis that has been in SAS for decades. You can create the plot by using the LINES option in the LSMEANS statement. The lines plot indicates which groups have mean differences that are not significant. For balanced data (or nearly balanced), it does a good job of summarizes which differences of means are not significant. For highly unbalanced data, there are other graphs that you can use. Those graphs will be discussed in a future article.
- Westfall, Tobias, and Wolfinger (2011) Multiple Comparisons and Multiple Tests Using SAS, Second Edition.

13 Comments
Thanks for this explanation. I hadn't seen the lines plot before Warren's post. My initial reaction is I find it a little bit confusing that the vertical "axis" is categorical, even thought the values are continuous. And my eye immediately wanted to see the bar length as indicative of a range. I wonder if I would like it more of the axis was scaled by the values. And of course it would be nice to see each group's mean and some estimate of it's variance. I look forward to seeing your follow-up post with alternatives!
Thanks for the comments. I agree with your criticisms. Yes, the vertical axis represents groups, so the axis is discrete. One reason is to reduce overplotting of labels for groups that have nearly the same mean. Another reason is to maintain compatibility with the tabular version of this display.
Rick,
There are two "datalines;" in your code which would lead to an error when running your code.
Fixed. Thanks.
How could I give letters to check significant differences for each treatment in line chart
Use the LINESTABLE option. In addition to the Lines PLot, it will create a table that displays letters. Groups with the same letter have LSMEans that are not significantly different.
I keep getting an error when I try this
The first paragraph twice states that this feature is new in SAS 9.4M5, so that is the most likely source of your error. If you are using SAS 9.4M5 and still get an error, post your code and error message to the SAS Support Communities.
I get the following message in my linestable output
The LINES display does not reflect all significant comparisons. The following additional pairs are significantly different:
how can I get all the comparisons to display?
If I understand your question, this situation is discussed in the documentation of the LINES option on the LSMEANS statement.
Hi Rick,
I frequently get the message at the bottom on the lines table stating "The LINES display does not reflect all significant comparisons. The following additional pairs are significantly different:" even with a balanced design experiment, when I analyze count data in Glimmix with the negative binomial distribution. Furthermore, the "additional pairs are significantly different" part usually makes no sense. If I manually log transform the data first and then run it as a normal distribution, the lines problem usually goes away. Is there something specific to Glimmix where it has issues generating lsmeans when the data have been log transformed (link=log) to be analyzed as a negative binomial distribution?
Thanks for your thoughts on this!
My first comment is that I prefer the PLOTS=DIFFPLOT option because a diffogram does a better job of showing significant differences. My second comment is that the documentation for the LINES option explains several situations in which that message appears. Unfortunately, I don't have a lot of experience with using PROC GLIMMIX to analyze negative binomial data, but I will ask a colleague who has more experience than I do.
The analysis of a log-linked negative binomial model is not at all equivalent to log-transforming the response and modeling it as normally distributed. I would not expect those results to be the same, and the latter is probably not valid for analyzing count data. Note that, for most generalized linear models, the variance is not assumed to be constant. That might also come into play in explaining the message as well as any inequality of group sizes.