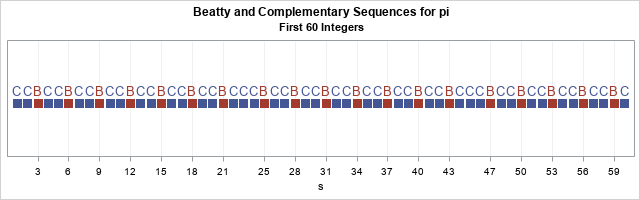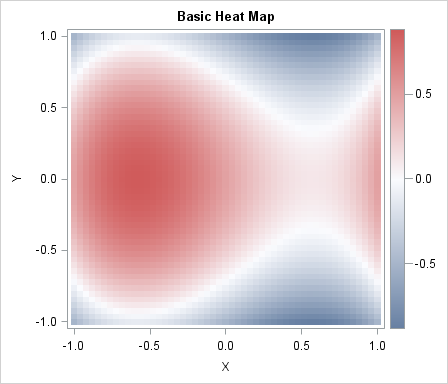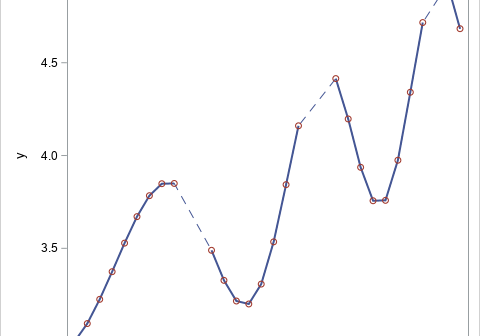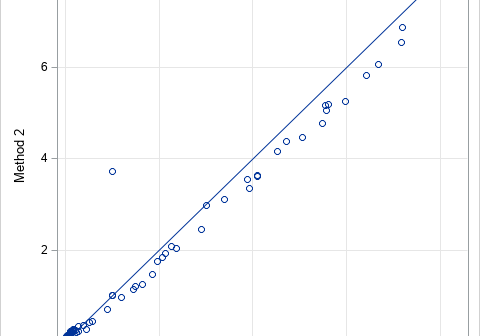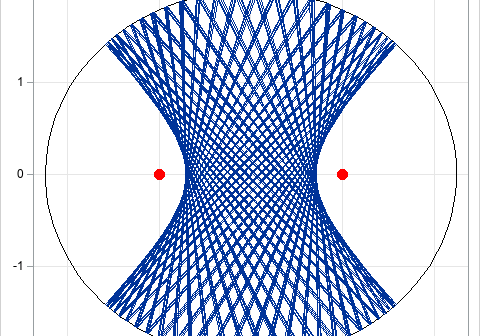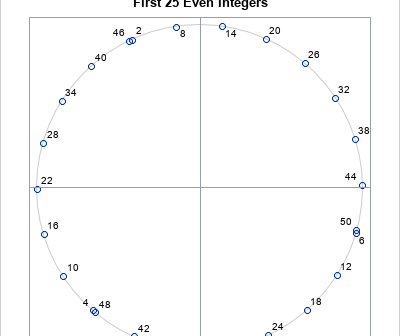
On this Pi Day, let's explore the "πth roots of unity." (Pi Day is celebrated in the US on 3/14 to celebrate π ≈ 3.14159....) It's okay if you've never heard of the πth roots of unity. This article starts by reviewing the better-known nth roots of unity. It then