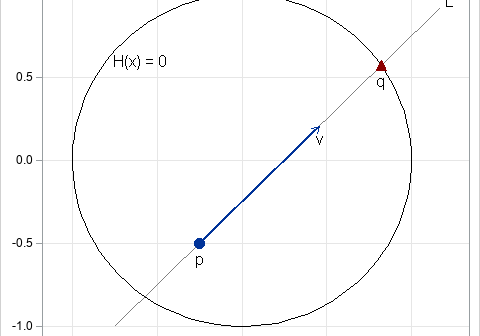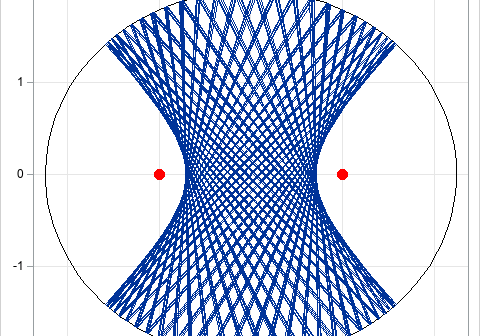
I recently showed how to find the intersection between a line and a circle. While working on the problem, I was reminded of a fun mathematical game. Suppose you make a billiard table in the shape of a circle or an ellipse. What is the path for a ball at