Last week I had the pleasure of delivering a one hour web lecture for the American Statistical Association on "Why Are Forecasts So Wrong? What Management Must Know About Forecasting."
I find it helpful (both for myself and the audience) to follow up with written responses to all questions submitted during the webinar. This way I can respond to those questions we didn't get to during the session, and provide more coherent responses to those questions I answered live.
Why Are Forecasts So Wrong? Q&A (Part 1)
Q: You spoke quite a bit on the validity of simple forecasts. Are the charts on slide 7 indicative of this? Please elaborate since fit error improves in Model 3.
A: This slide illustrates four increasingly complex models being used to forecast week 7, given observed values of 5,6,4,7 units for weeks 1-4.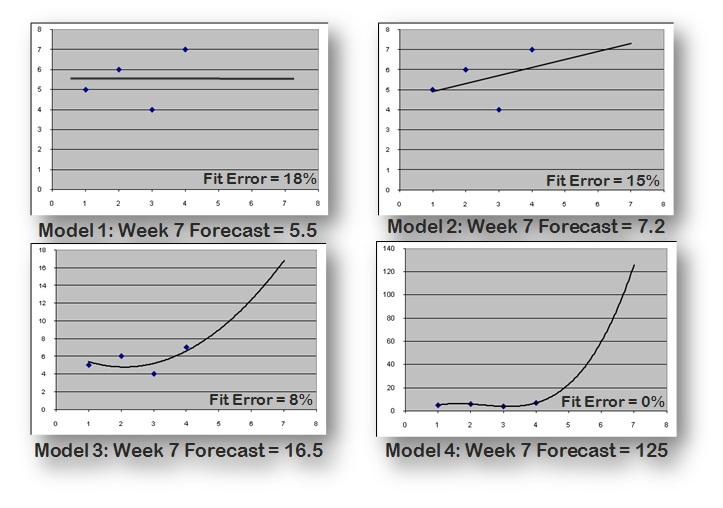
A large body of research has shown that simple methods tend to forecast the future as well (or better) than more complex methods. While complex methods can fit the history better – as we see in this example – there is no guarantee that better fit to history delivers more accurate forecasts of the future. Since our job is forecasting the future (not fitting history), it is good practice to begin with simple methods and add complexity only when there is good reason to believe they will result in more accurate forecasts.
In this example, we don’t know what the actual value is for week 7, so we don’t know which model generated the most accurate forecast. However, with no other information, the first two models (mean and linear trend) appear to be more appropriate than the quadratic or cubic models.
Q: You mentioned that sometimes manual adjustments make forecasts worse but also that we need to make the demand forecastable. What if the manual adjustment is made is due to learning something new about the forecasted demand?
A: Let me distinguish two separate issues raised in this question.
Making the demand forecastable is a general principle, suggesting that you look for ways of reducing the volatility in your customer demand patterns. As we saw in the “comet” charts, reducing volatility generally results in more accurate forecasts. So anything an organization can do to smooth demand patterns (e.g., by removing the incentives that create volatility), will likely result in more accurate forecasts, lower costs, better customer service, etc. There are lots of good results from more stable and more predictable demand.
There is plenty of evidence that a surprisingly large proportion of manual overrides to statistical forecasts just make the accuracy worse. Any decently performing model should probably be left on its own. However, if there is new information that was not incorporated in the model and can have a meaningful impact on demand, then yes, it is completely appropriate to make manual adjustments.
My suggestion is to limit your manual adjustments to situations where you have good reason to believe the statistical forecast will be inaccurate by a meaningful amount. If there will only be a small impact, then an override is probably not even worth the effort. A question to ask yourself is whether any decisions or actions will be changed as the result of your override. If no behavior will change because of the override, don’t waste your time making it.
Q: How would you suggest that we communicate to management/clients that forecasts are by nature prone to error? In my experience, clients expect forecasts to be 100% accurate.
A: It is true that clients (any user or recipient of the forecast) tend to have unrealistic expectations for the accuracy that can be achieved. The only cure for this is education, so they understand the limits of what forecasting can deliver.
Coin tossing examples help illustrate the point that accuracy is ultimately limited by the nature of the behavior being forecast. You can also create a comet chart with the client’s data, so give a sense of what range of accuracy has been achieved at various levels of volatility for their products. Also, it is informative to calculate the accuracy that a naïve model (random walk (i.e. no-change model) or seasonal random walk) or other simple model like moving average or single exponential smoothing. It is often difficult to improve very much over a very simple or naïve model. That is just the reality of forecasting the future.
