Over at the SAS/IML Discussion Forum, someone posted an interesting question about how to create a special matrix that contains all combinations of zeros and ones for a given size.

Specifically, the problem is as follows. Given an integer n ≥ 1, produce a
matrix with 2ⁿ rows and n columns that contains all combinations of zeros and ones of length n. For example, the following matrix is a solution for n = 3:

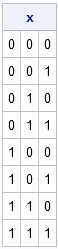
I can think of three ways to accomplish this task. The first algorithm builds the matrix by columns; the other algorithms build the matrix by rows and, although they are less efficient, they have the advantage of being suitable for a DATA step implementation.

EDIT: As of SAS/IML 12.3, you can use the EXPANDGRID function to create a binary matrix that contains all binary combinations, For example, x = ExpandGrid(0:1, 0:1, 0:1);.

Building the Matrix by Columns

If you study the example matrix, you will discover a pattern to the columns:

1. For the first column, the first half of the entries contains zeros and the second half contains ones.
2. For the second column, one-fourth of the entries are zeros, then one-fourth ones, and then the pattern repeats.
3. For the third column, one-eighth of the entries are zeros, and then one-eighth ones, and then the pattern repeats until all rows are filled.

This suggests an algorithm: for each column, build up a vector that consists of a number of zeros followed by the same number of ones, and then repeat this pattern until all rows are filled. The length of the pattern depends on the column number. The following module implements this algorithm:

proc iml;
 
start GetAllZeroOneComb(n);
   rows = 2##n;
   /** construct one column at a time **/
   x = j(rows, n);
   do j = 1 to n;
      PatLength = 2##(n-j); /** length of each pattern **/
      PatRepl = 2##(j-1);   /** number of patterns **/
      pattern = j(PatLength,1,0) // j(PatLength,1,1);
      x[,j] = repeat(pattern, PatRepl);
   end;
   return( x );
finish;
 
x = GetAllZeroOneComb(3);

You can use the GetAllZeroOneComb module to generate matrices of any size. However, because the number of rows grows as 2ⁿ, the algorithm will run out of memory for moderate-sized values of n.

Building the Matrix by Rows

If you study the example matrix, you will also discover a pattern to the rows: the ith row is the binary representation of the integer i – 1. Therefore an algorithm is to generate the binary representations of the sequence 0:2##n-1.

I could write a SAS/IML module that takes a number and returns a row vector that contains the binary representation of the number, but instead I'm going to leverage the power of SAS formats. SAS has a BINARYw. format which converts a number into a string that contains the binary representation of the number. (You can use the PUTN function to apply a SAS format to elements of a SAS/IML matrix.)

You can then use the SUBSTR function
to pick off each character in the binary sequence and the seldom-used NUM function to convert the character into a numeric zero or one. The following module implements this algorithm:

start GetAllZeroOneCombByRow(n);
   rows = 2##n;
   /** construct one row at a time **/
   x = j(rows, n);
   format = "binary" + strip(char(n)) + ".";
   do i = 1 to rows;
      s = putn(i-1, format);
      do j = 1 to n;
         x[i,j] = num(substr(s,j,1));
      end;
   end;
   return( x );
finish;

I don't like this algorithm for SAS/IML programming because there are no vectors in sight. This is an algorithm that plods through the matrix cell-by-cell and fills in the appropriate zero or one. It is better suited for the DATA step than for SAS/IML. In fact, the DATA step implementation is almost identical, except would use an array of variables instead of columns of a matrix.

Building the Matrix by Using All Combinations

If the order of rows in the matrix is not important, then you can implement another row-wise algorithm. I won't implement it here, but you can use the ALLCOMB function to look at all combinations of n elements taken k at a time, and use those combinations as locations for the ones in the matrix. For example, one of the "3 choose 1" combinations is (2), and this combination corresponds to the row {0 1 0} which has a one in the second location. One of the "3 choose 2" combinations is (1, 3), and this combination corresponds to the row {1 0 1}.

Perhaps you can think of another algorithm? If so, describe it in the comments or on the original thread.