 Every year on March 14, we celebrate Pi Day in recognition of the famed mathematical constant π. This date in the format MM/DD is 3/14 which corresponds to the first three digits of the π value 3.14.
Every year on March 14, we celebrate Pi Day in recognition of the famed mathematical constant π. This date in the format MM/DD is 3/14 which corresponds to the first three digits of the π value 3.14.
As you all know, π represents the ratio of a circle's circumference to its diameter. Therefore, we can derive a circle's circumference C from its diameter d using the following famous formula:
C = πd (or C = 2πr using radius r).
While it is impossible to overstate the significance of π in its fundamental and legendary role of being a constant representing the circumference/diameter ratio, its usage for area and volume measurements is not as much of a “settled science” as you may think. In this post, I dare to debunk the notion of π being an inherent component of the omnipresent circle area and sphere volumes formulas:
A = πr2 = π/4 ⋅ d2
V = 4π/3 ⋅ r3 = π/6 ⋅ d3
Believe it or not, we can significantly simplify these formulas by getting rid of π altogether. Wanna know how? Just sit down, relax, open your mind and fasten your seat belt.
Misnomer alert!
(Definition: A misnomer is a wrong or inaccurate use of a name or term.)
Let’s start with some questionable and overreaching semantics in algebra. Have you ever noticed that we call a number to the power of 2 as the number squared? Similarly, we call a number to the power of 3 as the number cubed. However, besides 2 and 3, we treat all other exponents Np equally by saying "N to the power of p".
Here is how Wikipedia explains this exponentiation phenomenon:
“The expression b2 = b ⋅ b is called "the square of b" or "b squared", because the area of a square with side-length b is b2.
Similarly, the expression b3 = b ⋅ b ⋅ b is called "the cube of b" or "b cubed", because the volume of a cube with side-length b is b3.
Wait a minute! Exponents b2 and b3 are mathematical operations from the Algebra Department. They are just abbreviations for multiplication operations and have nothing to do with geometrical shapes and exist independently from geometry and area/volume calculations.
The same semantical problem persists with the reverse terms square root and cube root. All natural numbers N have their corresponding root operations, which we call the Nth root. So why do we need this suggestive verbal association of the area/volume measurement units to squares and cubes?
Moreover, the very word “area” itself is often replaced by square footage, square mileage, or square something thus further implying that areas and squares are synonymous. To me this is like calling a round wheel “a rolling square”.
Overall, this square/cube-centric language insidiously conditions our minds into thinking only in terms of squares and cubes regarding the units of area and volume measurement.
Why do we measure area of a circle in squares?
We all know from middle school’s elementary geometry that area of a circle of radius r is A = πr2 (or A = πd2/4 using diameter d since r = d/2). Many famous ancient mathematicians from Archimedes to Eudoxus of Cnidus to Hippocrates of Chios have proven this formula. There is also a multitude of its proofs using modern methods rooted in trigonometry and calculus.
However, all these methods have one funny thing in common. It is the presumption that an area must be measured in squares (square inches, square meters, square miles, etc.). Think about it for a minute: for thousands of years we have been measuring round areas by the number of squares with a side=1 covering that round area. C’mon! We invented the wheel, electricity, engines, airplanes, telephone, radio, TV, computers, spaceships, artificial intelligence and more, but we are still measuring round areas in squares!
It makes perfect sense measuring rectilinear areas in square units – they are a good fit for each other. But measuring round areas in squares?! What would you say if in reverse we were measuring square areas by the number of round coins covering them? How is that not as good as the opposite?
Introducing circular units of areas
Wikipedia defines area as "the quantity that expresses the extent of a region on the plane or on a curved surface... It can be measured by comparing the shape to squares of a fixed size." Sure, it can. However, it does not have to be measured in squares (square units).
Defining units of measurement is totally arbitrary. All we need is a well-defined gauge. For example, we have a variety of length units such as foot (derived from the size of the human foot), inch (derived from the width of the human thumb), meter (derived from the Greek word μετρέω - measure, count) and so on. They are all convertible to each other, but their definitions are quite different.
When it comes to the units of area, it can be a square, a rectangle, a circle, an oval, a star, even a snowflake or any other two-dimensional shape of a specified size as long as its definition is clear and unambiguous.
Without further ado let’s define a circular unit of area as an area of a circle with the diameter d=1 unit of length (inch, foot, meter, etc.).
Measuring circle areas in circular units
In order to measure areas of different sized circles, we do not need to count the number of these single unit circles placed side by side within the measured circle. We just place these two circles concentrically and expand or shrink our gauge circle until they align. Here is a visual to illustrate this:
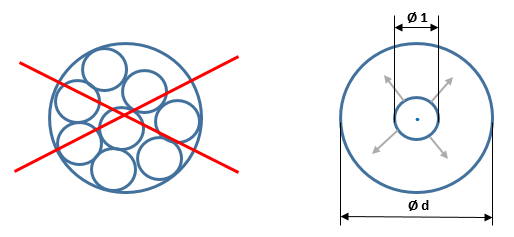
For a circle with the diameter d, we can express its area measured in the circular units Ac using the following formula:Ac(d) = d ⋅ d = d2
I would not call d2 as "d squared" here. The power of 2 is an indication of two-dimensional area while d is a one-dimensional length.
Let’s prove this formula. Suppose As(d) is a circle area with diameter d in square units and Ac(d) is the circle area in circular units.
As we know As(d) = πr2 = π (d/2)2 = (π/4)d2. For the same circle its area in circular units is Ac(d).
For d=1, we have As(1) = πr2 = π (d/2)2 = (π/4)d2 = π/4. The same circle area represents 1 circular area unit Ac(1)=1.
Therefore, Ac(d) = Ac(1) d2 = d2, that is we effectively eliminated π from the circle area calculation:
Measuring squares in circular units
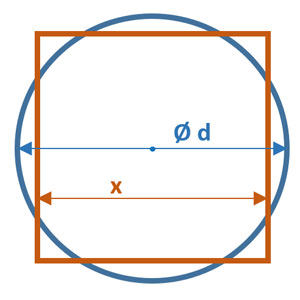
At the same time, π is not the kind of number to easily get rid of. Similar to the law of conservation of energy, there is probably a law of conservation of π: whenever we get rid of it in one place, it appears in another place.
Let’s suppose we have a square with side length of x. Then its area in square units will be As(x) = x2. If we take a circle of the same area we get the following equation As(x) = x2 = (π/4)d2. From here d2 = (4/π)x2. Since d2 represents the number of circular units Ac we can say that the area of a square with side length of x in circular units is Ac(x) = (4/π)x2:
Notice that π-wise these two formulas for area, Circle_Area=(π/4)d2 [square units] and Square_Area=(4/π)x2 [circular units], are literally upside-down version of each other.
Spheric units for 3D geometry
We can apply the exact same approach to measuring volumes of three-dimensional objects. In the cubic unit’s paradigm, we define one cubic unit of volume as a cube with a side of one unit of length. Then the volume of a cube with a side of x is Cube_V=x3 [cubic units] and the volume of a sphere with a diameter of d=2r is Sphere_V = (4/3)πr3 = (π/6)d3 [cubic units].
Alternatively, in the spheric unit’s paradigm we define one spheric unit of volume as a sphere with a diameter of one unit of length. Then the volume of a sphere with a diameter of d is:
and the volume of a cube with a side of x is:
Again, here I would not call d3 and x3 as "d cubed" and "x cubed" since the power of 3 is indicative of three-dimensional space while d and x are one-dimensional units of length.
Similarly to area calculations, π-wise these two formulas for volume, Sphere_Volume=(π/6)d3 [cubic units] and Cube_Volume=(6/π)x3 [spheric units], are literally upside-down version of each other.
Is this practical?
If you still doubt the validity and/or practicality of my geometric deductions, check out circular mil units of area adopted for wire size measurement by the US National Electrical Code (NEC) and the Canadian Electrical Code (CEC).
A circular mil (cmil) is a unit of area equal to the area of a circle with a diameter of one mil (one thousandth of an inch or approximately 0.0254 mm).
While applied just to one particular unit of length – mil, it is exactly the same circular units of area concept as described in the previous sections.
As you can see, electrical engineers have figured out a use for circular units, perhaps because they are dealing with electrical wires, which are predominantly round in their cross section. Since electrical conductivity of wires is directly proportional to their cross-section area, it is just more convenient to use circular units (without π) for calculating the cross section and ultimately electrical conductivity. The same is true for the throughput capacity while transporting any substance via pipes (water, gas, oil, etc.) or moving blood through the blood vessels.
There are many other applications dealing with the circular shapes and spherical objects. In all these cases, it makes more sense to measure areas in circular units rather than squares and measure object volumes in spheric units rather than cubes. Take for example physics (gravitational, electrical and magnetic fields), astronomy (planets, stars, comets, and orbits), geology (areas around earthquake epicenters), telephony (areas of cellular tower coverage), etc.
Agree or Disagree?
If we are measuring circle areas and sphere volumes in "circles" and "spheres" (circular and spherical units), then we can call d2 "d circled" and we can call d3 "d sphered", because now d2 represents the area of a circle with diameter d, and d3 represents the volume of a sphere with diameter d. (Here, I just applied the same logic as how the conventional terms "d squared" and "d cubed" were coined - see Misnomer alert! section above.)
Your thoughts, comments
I would like to hear from you. What do you think about all this? Please share your thoughts in the Comments section below.
ACCESS FREE SAS® SOFTWARE | SAS® OnDemand for Academics
16 Comments
At age of 57, I am doing an online course to refresh my math and algebra skills. When I saw that the function "x squared + y squared" forms a perfect circle as a graph, I was surprised and noted that there seems no need for PI at all to describe a circle, and since both values are squared, I conclude that the resulting value is the area of the circle.
Great observation, Ralf! As you know, π is nothing more than the constant ratio of a circle's circumference to its diameter. The function you are talking about, x^2 + y^2 = r^2 is in essence the Pythagorean theorem.
Hi Leonid,
Wow! This is a mind-blowing demonstration that, in mathematics (and elsewhere), we tend to take our reference framework for granted ... and that, if we are able (in this case, definitely thanks to you :-)) to recognize that we are using a reference framework it allows us to change and open our mind, making it (hence us) more free. Thank you!
#thinkoutsidethebox
#helicopterview
#originality
Thank you, Anne, for your feedback. Indeed, our minds are often locked into certain ways of thinking ("reference framework"), and any move out or an attempt to break loose is met with resistance either from within or from without. You got it right and I like how you connected "freeing minds" to "freeing people". It's a great generalization.
Some people actually created a voxel 3D rendering system based on spheres, that is, modelling all 3D objects as collections of spheres of various sizes. Spheres have a wonderful property what you do not need to take into account their orientation, only position and size. It is very useful when you have to determine if a ray intersects the object or not. So constructing 3D volumes from spheres makes some practical sense.
Thank you for reinforcing and expanding my point, Anton. I would just add that similarly to spheres in 3D, circles have the same wonderful properties in 2D. In many ways, both circles and spheres are the perfect geometric objects.
Very nice! We can't get rid of Pi - it is always somewhere! Thank you, Leonid! Great post for square minds - eyes are easily getting round reading this! 🙂
Thank you, Elena! Hope "square minds" get well rounded too 🙂
Hi @Leonid, this is an interesting blog, I kept asking myself whether the same logic can be applied when it comes to getting the Circumference, or the circular logic only applies to Area?
Good question, Daniel.
We can't apply the same logic to the circumference as long as both, circumference and diameter are measured in the same linear units of length. Therefore, π is a "king" there, as it represents a fundamental constant - the ratio circumference/diameter. In case of areas (volumes) we can vary definitions of the gauge thus arriving at different formulas.
However, if we measure length in non-linear units (e.g. logarithmic scale) then we can arrive at various circumference formulas.
But, but, but..,I need π. It's my password to get into my house.
I hope your house is more like a square/cube, and not a circle/sphere. In this case, you got your πassword - just read this article closely (there is a "law of conservation of π" in it) 🙂 .
I can picture you on a Professor's platform lecturing, challenging, and educating.
I hope that you publish a SAS book someday.
Brain teaser!
Enjoyed it.
Thank you, Deborah! I am glad you enjoyed it.
Great post, Leonid Batkhan. I will admit at first I thought it might be an early April fool’s post. But as I kept reading, it hit me, “nope, this isn’t a joke… and I’m going to learn something interesting.”
Thank you, Quentin! Quite a natural progression, I would react the same 🙂