“In God we trust, all others must bring data”

- Dr. W. Edwards Deming

En el mundo de los sommelier se denomina cata a la acción encaminada a examinar, valorar, comparar o identificar vino (te o café, etc.) mediante el empleo de un análisis realizado con nuestros sentidos: es lo que llamamos el análisis sensorial. Una de las pruebas sensoriales que se realiza es aquella en la que el catador debe evaluar la calidad como aceptable, dudosa o rechazada. De igual manera, en la gestión de riesgo de mercado, el VaR (cuyo concepto explicamos en la primera entrega del “Sommelier del Riesgo”) que utilicemos se lo debe examinar con el fin de verificar la validez del modelo aplicado. De acuerdo a las mejores prácticas del mercado y a las recomendaciones establecidas por el Comité de Basilea, la aplicación de modelos VaR debe estar acompañada por un proceso de validación o backtesting.

Backtesting

El backtesting para riesgo de mercado es una prueba retrospectiva que compara la pérdida realizada para cada periodo con el VaR estimado, en donde las grandes y persistentes diferencias en estos valores sugieren que las suposiciones metodológicas no logran captar el riesgo real que está presente.

Haciendo referencia a la Comunicación local “A 5203” emitida por el Banco Central de la República Argentina, se debe llevar a cabo un programa periódico que compare los resultados realizados con las predicciones de estos, con el objetivo de cotejar si el número de pérdidas mayores a las predichas está en línea con lo esperable al nivel de confianza, establecido en el cálculo del VaR.

Siguiendo esta línea, en cuanto al cálculo del VaR, el Comité de Basilea propone en testear el número de violaciones (pérdidas mayores a las predichas) efectivamente acontecidas durante los últimos 250 días en relación con el número de violaciones esperadas de acuerdo a un nivel de confianza del 99%.

Clasificación

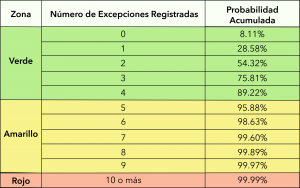
Para ello, el método clasifica los resultados del backtesting en “3 zonas” a los efectos de poder evaluar la validez del modelo. El objetivo de la clasificación por zonas es alcanzar un balance entre cometer el error de tipo 1 (es decir, rechazar un modelo válido) y el error de tipo 2 (es decir, aceptar un modelo no válido).

• De esta forma, si se presentan de 0 a 4 excepciones observadas, el modelo cae sobre la zona verde y se define como válido en tanto que la probabilidad de aceptar un modelo no válido resulta relativamente baja.
• Dentro de la zona amarilla, cuyo espectro de excepciones va de 5 a 9, los resultados podrían ser producidos tanto por un modelo válido como por uno no válido con relativa alta probabilidad. De esta forma, la zona intermedia permite el estudio del modelo utilizado sin necesidad de que sea rechazado automáticamente.

¿Por qué fallan los modelos?

Los cuatro grandes motivos por los que un modelo puede estar fallando son:

• 1. La integridad básica: el modelo no es capaz de medir correctamente el riesgo de las posiciones o existe un error en el cálculo de las volatilidades y correlaciones.
  2. La precisión del modelo no resulta adecuada en la medición del riesgo de algún factor.
  3. Movimientos de mercado no anticipados.
  4. Cambios estructurales del portafolio, posteriores al cálculo del VaR.
• Por último, la zona roja indica un claro problema con el modelo del VaR, dada la baja probabilidad de que un modelo válido genere 10 excepciones dentro de una muestra de 250 observaciones. Como resultado, la zona roja lleva a un rechazo automático del modelo.

Tipos de pruebas de backtesting

Siguiendo esta línea, a continuación se detalla el marco teórico a la hora de llevar a cabo pruebas posibles de backtesting en la gestión del riesgo de mercado:

• Unconditional Coverage Test (cobertura incondicional): Sugerido por Kupiec (1995), es la prueba más ampliamente conocida basada en tasa de excepción. Denominamos excepción cuando la pérdida real excede a la que fue establecida por el VaR de acuerdo al nivel de confianza seleccionado. El objetivo consiste en determinar si la tasa de excepciones observada es significativamente diferente de la tasa de excepciones sugerida por el nivel de confianza. En otras palabras, la prueba de cobertura incondicional testea la hipótesis nula de que las infracciones ocurren con una probabilidad consistente con el intervalo de confianza elegido para el VaR. Por lo tanto, si el VaR se mide a un intervalo de confianza del 95% y la muestra de la prueba es de 100 días, la prueba de cobertura incondicional probará si el número de violaciones reales es consistente con los 5 esperados.De esta manera, si excede el valor crítico de la distribución, la hipótesis nula será rechazada y el modelo debe ser sometido a consideración ya que muestra indicios de no ser el modelo adecuado.

• Independence test: La prueba de independencia prueba si las violaciones del VaR son verdaderamente independientes. Es decir, la hipótesis nula es que no hay un patrón predecible para las violaciones de VaR. Con una muestra de prueba de observaciones diarias, el Independence test observará si es tan probable que tenga una violación de VaR, si hubo una el día anterior o si no hubo una el día anterior y como lo es.

• Conditional Coverage Test: Christoffersen (1988) propone una prueba de relación de probabilidad condicional de cobertura (CC) que combina la prueba de cobertura incondicional y la prueba de independencia. Este aplica el mismo esquema que Kupiec agregándole, en este caso, el objetivo de examinar si la probabilidad de una excepción en un momento “t” depende del resultado del momento “t-1”. Es decir, intenta probar la existencia de independencia entre cada una de las excepciones. Con el VaR medido a un intervalo de confianza del 95% y una muestra de prueba de 100 días, la prueba de cobertura condicional probará que el número de violaciones reales sea consistente con los cinco esperados y que estas violaciones sean independientes entre sí.

En resumen, hasta aquí podemos decir que la prueba de validación del VaR es una comparación del peor de los casos (VaR) y el P/L realizado durante un período de tiempo específico. Una prueba exitosa mostrará que:

• El número de violaciones (pérdida realizada> pérdida proyectada) es consistente con el intervalo de confianza especificado (prueba de cobertura incondicional)
• Las violaciones son independientes entre sí (prueba de independencia)
• Las 2 hipótesis anteriormente planteadas, son verdaderas al mismo tiempo (prueba de cobertura condicional)

Otros tipos de pruebas

Además de los test estadísticos mencionados, existen otros test como:

• Mixed Kupiec Test: Este test, propuesto por Haas (2001), continúa profundizando en el análisis del grado de independencia de las excepciones, teniendo en cuenta, en este caso, el tiempo que existe entre las mismas. Es decir, a diferencia de observar sólo si una excepción hoy depende del resultado del día previo (tal cual Christoffersen) observa si es posible que dependa, por ejemplo, de la excepción acontecida hace una semana. Es por esto entonces, que esta prueba es potencialmente capaz de capturar más formas generales de dependencia.
• Duration Base Test: Christoffersen y Pelletier (2004) proponen pruebas fundadas en la duración, las cuales se basan en la distribución de las duraciones, o períodos entre violaciones. Con un modelo de VaR correctamente especificado, las duraciones deben tener una media de 1 / a y sin memoria.  La propiedad sin memoria significa que la probabilidad de una violación en el próximo período es independiente del número de períodos desde la última violación. Las propiedades de la distribución de Weibull hacen que sea propicio para su uso en pruebas de razón de verosimilitud basadas en la duración de la cobertura incondicional, la independencia o la cobertura condicional. Además, se ha demostrado (Christoffersen y Pelletier 2004) que las pruebas basadas en la duración tienen más poder que las pruebas de relación de probabilidad descritas anteriormente en este capítulo.

Esta entrega del “Sommelier del Riesgo” tuvo en cuenta las pruebas de backtesting que se pueden ejecutar en el motor de cálculo de SAS, denominado Risk dimensions. Cabe destacar, que actualmente el motor de cálculo se complementa con la solución denominada High Performance Risk que permite agregar los resultados obtenidos en memoria. Esto permite manejar cálculos complejos muy rápidamente y almacenar grandes volúmenes de resultados, por lo que podemos investigar información de riesgos utilizando jerarquías bajo demanda casi en tiempo real. Con respuestas rápidas y precisas a preguntas sobre P&L actuales y potenciales, flujos de efectivo y exposiciones de riesgo, se pueden tomar decisiones oportunas y bien informadas relacionadas con las carteras, incluso en entornos altamente volátiles y estresados. Más información sobre High Performance Risk en https://www.sas.com/en_us/software/high-performance-risk.html.

¡Los espero en la próxima entrega!