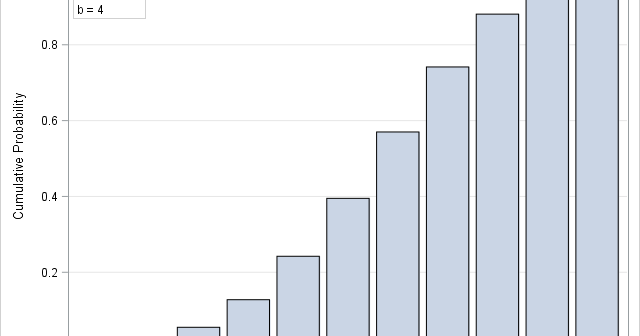
A statistical programmer read my article about the beta-binomial distribution and wanted to know how to compute the cumulative distribution (CDF) and the quantile function for this distribution. In general, if you know the PDF for a discrete distribution, you can also compute the CDF and quantile functions. This article