The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs
The multivariate normal distribution is used frequently in multivariate statistics and machine learning. In many applications, you need to evaluate the log-likelihood function in order to compare how well different models fit the data. The log-likelihood for a vector x is the natural logarithm of the multivariate normal (MVN) density
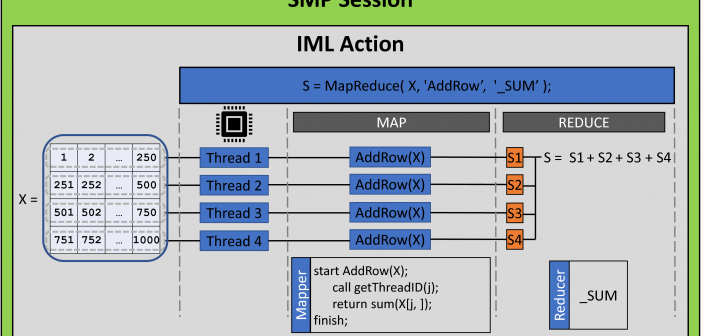
A previous article introduces the MAPREDUCE function in the iml action. (The iml action was introduced in Viya 3.5.) The MAPREDUCE function implements the map-reduce paradigm, which is a two-step process for distributing a computation to multiple threads. The example in the previous article adds a set of numbers by

The iml action in SAS Viya (introduced in Viya 3.5) provides a set of general programming tools that you can use to implement a custom parallel algorithm. This makes the iml action different than other Viya actions, which use distributed computations to solve specific problems in statistics, machine learning, and
