Blogs

Blogs

When is a Multilevel Model not appropriate?

0

By Chris Daman on SAS Learning Post April 24, 2013

I recently received this interesting question regarding Multilevel Models after one of my last blog posts:

Question: Can you tell me when a multilevel-model is not appropriate? I have data that by design is clustered but the random intercept in the null model is not significant. I have seen advice that says when this is the case all of your level 2 variation and thus the model for level 2 is over-fitted. I have heard others say that that doesn't matter use mlm anyway. Any response is most appreciated.

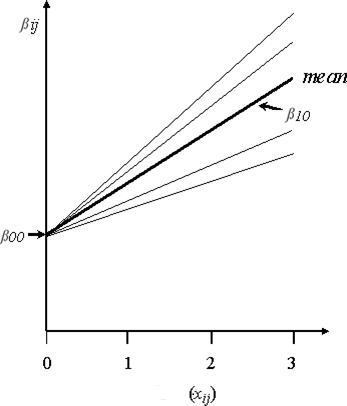
Answer: Is it possible that you might have random slope components? You could have a scenario where the variance component for the random intercept is not significantly different from zero, but the one for a random slope is. Visually, it would look like the picture below—you can see no variability is present for the group intercepts, but variability does appear to be present for the group slopes:

If you think you may have a random slope component, try fitting the model with your fixed effect predictors, a random intercept, and if appropriate a random slope component. After fitting the model and doing any necessary simplification, if none of the variance components for the random effects are significant, you would be assured you don’t need a MLM. Otherwise you may be assuming no random slopes are present without investigating it.

About Author

Chris Daman
Sr Analytical Training Consultant

Chris Daman is a statistical training specialist and course developer in the Education Division at SAS. She has more than 20 years of teaching experience—both nationally and internationally—in the fields of programming, statistics, and mathematics. Before joining SAS in 2005, she taught classes at N.C. State University and IBM, worked in the pharmaceutical and financial industries, and was a survey statistician at an international research organization. She currently teaches advanced statistics courses covering mixed models, generalized linear mixed models, hierarchical linear models, and design of probability surveys; in addition, she teaches design of experiments and analysis of complex data, such as longitudinal data, multilevel data, or data from complex surveys. She also teaches data mining classes, including applied analytics and advanced decision trees. She has a bachelor's degree in mathematics from the University of North Carolina at Greensboro and a master's degree in statistics from N.C. State University. Chris's favorite part of teaching is the interaction with the students. To keep them involved with the material and each other, she often uses a variety of teaching techniques (such as analogies, optical illusions, stories, object lessons, and group interactions) rather than the standard instructor-to-student lecture format. As a result, students give high ratings to her classes and typically include comments such as "I enjoyed Chris's teaching style very much. She did an excellent job of engaging the class and fostering interactions between all the students and herself" or "I love Chris's sense of humor. It definitely helps you get through complicated material". In her spare time, Chris enjoys dancing, reading, spending time with her family, and traveling.

Comments are closed.