我們將著重在討論價格為35000元(單位：美金)以下之汽車。首先我們先將資料做篩選。篩選與排序 =>變數 =>全選所有的變數拖曳至右邊 =>篩選條件 =>選擇「Invoice35000」 =>確定。完成之後，即可將所有價格小於35000元的汽車篩選出來。

在迴歸分析裡，我們有許多的方法來選擇我們的模型，如：向前選取法(Forward selection)、向後消去法(Backward elimination)、逐步選取法(Stepwise selection)、Mallows’ CP、R-平方(R-Square)、調整後R平方(adjust R-square)、Akaike information criterion(AIC)、Schwarz Bayesian Criterion(SBC)等。 分別介紹一下：

根據上一節最後選定的模型，我們做一次是否有共線性的問題。在此，我們有兩種方法來判斷，(1) 變異數膨脹因子（Variance Inflation Factor，VIF） (2) 共線性診斷(Collinearity Diagnostics)。當變異數膨脹因子>10或是共線性診斷>100時，表示有共線性的問題。

 最後，我們來介紹離群值與影響點。 一、離群值(Outlier)：尋找觀察值Y是否有離群值，我們可用Student殘差來看，其準則為： 二、影響點(Influential)： 1、DFFITS準則為： 2、DFBETAS準則為： 3、Cook’s Distance measure(Cook’s D)準則： 為了了解哪些筆資料有離群值或是影響點，我們再一次點「修改工作」=>選擇「預測」，先勾選「原始樣本」再勾選「診斷統計值」=>執行。 在分析資料時我們發現有兩筆資料(第178、179筆)在記錄時遺失氣缸數，故無法做任何的預測，所以我們將刪除。 首先我們先討論Cook’s D的情形，其圖形如下： 在圖示上，我們可以很明顯看到有似乎只有三筆影響點，配合上述Cook’s D的公式，當Cook’s D的值大於0.013時表示為影響點；因此，我們回到原始資料來查看是哪幾筆。在「結果-SAS報表」旁邊有「輸出資料」=>將資料拉至後方，我們可看到Cookd_EngineSize_log的值。 結果我們發現Cook’s D大於0.013的觀察值分別為：第6、12、47、65、103、105、108、109、149、295、208、297、298、303，共14筆。 接下來我們觀察DFFITS的情形，其圖形如下： 配合上述dffits的公式，當絕對值的diffits大於0.25時即為影響點，我們亦可以從原始資料來觀察。其影響點為：第6、12、47、58、65、93、103、105、108、109、147、149、242、260、295、208、297、298、303、313，共20筆。 透過兩種看影響點的方法，我們發現有14筆資料有重覆，而以DFFITS為標準則找出較多的影響點。 結論：根據迴歸式的估計結果可知當氣缸數較大、馬力較大、車身長度較長，而價格低一點、行走高速公路的油秏差一點，會得到較大的引擎CC數；但是我們將這些影響點列出發現有很明顯的不同。舉例來說，第109筆資料我們發現氣缸數非常的少(只有三個)，且馬力也是最小的，但是在油秏上卻非常的出色。又例如第105筆資料有最多的氣缸數(八個)，馬力非常好，而在油秏上卻表現的不差，在價格方面亦不是很高價…等。 根據上述的分析，除了有兩筆資料有遺失值我們刪除外，其他的觀測值雖為影響點(假設在建資料時沒有錯誤)，但我們仍不應將資料刪除，以反應真實的情形。

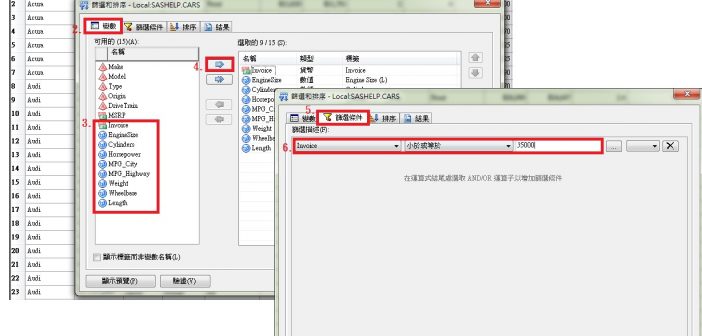
「混合模型」工作會讓各種混合線性模型符合資料，可讓您使用這些符合的模型對資料進行統計推論。 混合線性模型是標準線性模型的概括，概括的內容是允許資料呈現相關及非常數變異性。混合線性模型非常靈活，不僅可以建立資料平均值的模型，也可以建立其變異數與共變異數的模型。

在多變量分析中，主成分分析（Principal components analysis, PCA）是一種分析、簡化數據集的技術。利用原有的變數組合成新的變數，以達到資料縮減的目的，但卻能夠保留住數據本身所提供的重要資訊。由於主成分分析主要依賴數據提供的訊息，所以數據的準確性對分析結果影響很大。

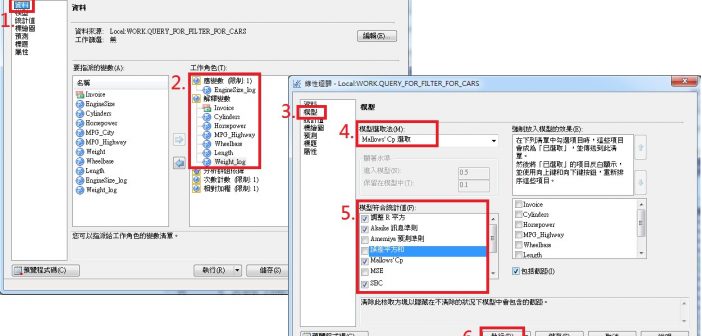
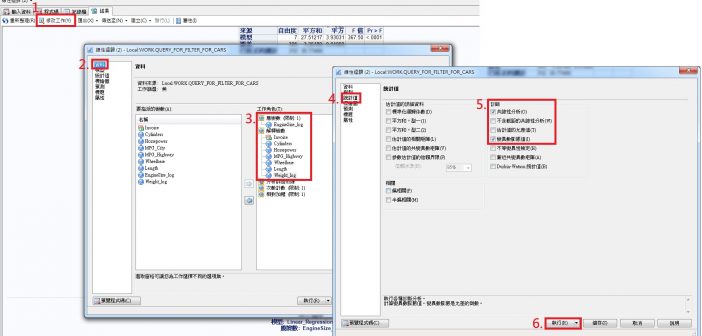
因子分析可執行各種公因子與成分分析及轉軸。輸入內容可以是多變量資料、相關矩陣、共變異數矩陣、因子模型或計分係數矩陣。 因子分析又稱因素分析，可以將一群彼此相關、較難解釋的變數，轉爲可概念化具解釋性的少數幾個因素，也可達到資料縮減與摘要的目的。每個變數由共同因素和獨特因素組成。 因素分析分爲兩種： 探索性因素分析 在因素個數、路徑都沒有限制下去尋找結構，一般來説，為研究量表或問卷建構效度，多屬於此分析 驗證性因素分析在已知研究方法或是有理論支持下去驗證假設是否適用 因素分析該怎麽做呢？ 估算共同性：計算變數之間的相關矩陣或共變數矩陣，變數的相關係數越強，越有可能歸在同一因素內 抽取因素：萃取共同因素並估計因素負荷量。常見抽取方式包含主成分分析法、及主軸因素法與最大概似法等 轉軸：轉軸可以讓因素負荷量更易於判讀，旋轉方式可分爲： 直交：因素之間彼此獨立，軸間夾角為 90 度，如變異最大旋轉法、四方最大旋轉法 斜交：因素之間仍有相關，如 Promax 旋轉法 最後，決定因素個數，對其解釋與命名，可以參考因素負荷量較大來對因素命名。 因素分析講師說明與範例一:  

群集分析是將相近的樣本聚集在一起，分成集群。

對於包含一或多個屬量變數及定義觀測值群組之分類變數的一組觀測值，「判別分析」工作會開發判別準則，將各觀測值分類為其中一個群組。由此資料集導出的判別準則，可於判別函數的同一個執行期間，套用到第二個資料集。 您可以使用這個工作，對自然界中發現的觀測值進行分類。例如，您可建立 SAS 資料集，其中包含 36筆植物的種類(5類)和4個不同的測量值。您可以使用此資料，將每一筆植物分類為5個種類之一的最佳分類變數，找出判別函數。

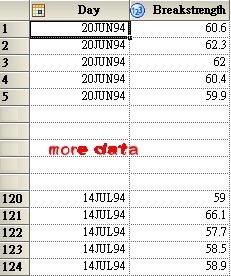
Shewhart 圖表是Shewhart (1891-1967) 是貝爾實驗室的物理學家，於 1924 年發表了此方法。 管制圖的立論概念是，任何生產流程中的自然變異均可透過一組管制界限來量化，若變異超出這些界限，即表示流程中有所變化。是業界在研究生產流程的輸出變化時最常用的統計式品管法。 Shewhart 圖表是一種圖形化的分析工具，可用以判斷程序是否符合統計控制。「平均值與全距圖表」工作可建立子群組平均值與子群組全距的平均值與全距圖表。這些圖表可用以分析製程的集中趨勢與變化性。