在資料為常態假設下，欲比較兩個群體的平均數是否有差異時，我們可以使用t-test檢定之。但若我們欲比較多個群體的平均數是否有差異時，則必須使用變異數分析(ANOVA)的方法來判別。 若分析的結果顯示出多組平均之間有差異時，這時我們可以更進一步進行兩兩平均數間的差異比較。 而變異數分析需有三項假設前提(獨立、常態、均質)，在進行分析時也要先檢定資料是否有符合這三項假設。
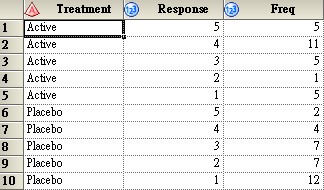
在執行變異數分析時，有獨立、常態性、均值三大假設。若資料不符合常態或均值假設時，此時我們可以利用無母數的方式，檢定母體中位數是否有差異來替代檢定母體平均數，則我們就不需資料為常態性或均值的前提假設。
在分析資料中我們若遇到兩個數值型變量時，我們最先採取的分析方法是製作這兩變量的散佈圖。從散佈圖中可以大略看出此兩數值型變量之間的關係，是遞增、遞減、成線性或是非線性。以下將帶領大家如何在SAS EG裡繪製散佈圖來表現雙數值型變量之間的關係。
在SAS EG的「區域圖」工作可建立區域、雲線、步階或覆疊圖，以顯示兩個變數間的數學關係。 區線下的區域會以圖樣或顏色組合填滿，以產生視覺化的效果。
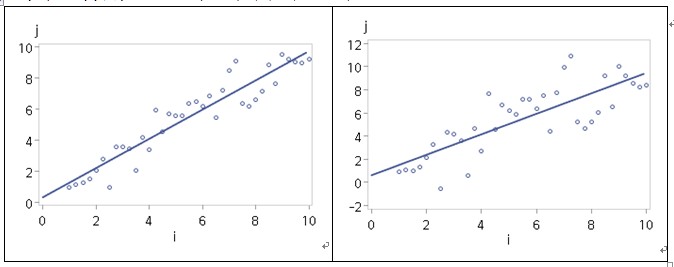
在做迴歸分析前，我們須先了解兩數值型變數間是否有呈現線性相關，最簡單的方式就是觀察兩變數的散佈圖。以下面兩張圖為例，雖然兩者均呈現線性相關，但相較於左圖而言,右圖的資料分布與迴歸線較為離散，所以我們可以因此而認定右圖資料不適合做迴歸分析嗎？也由於散佈圖的解說是很主觀的，如果我們只靠圖形來判別資料適不適合做迴歸分析，可能每個人的解讀結果都不相同。這時我們就需要有一個客觀的判斷準則--統計量。
典型(正準)相關用來檢查一組 X 變數的線性組合與一組 Y 變數的線性組合之間的關係。例如：您可以使用正準相關工作，判斷一組工作特徵與一組員工滿意度評量之間的對應程度。
迴歸分析是統計學上常用的分析方法，主要在建立一個函數（最能夠代表變數間的所有觀測資料），並用此函數來代表應變數和自變數之間的數學模式，以便觀察特定的變數來預測我們所感興趣的變數。若特定的變數（X）和有興趣的變數(Y)的數目都為一個，則我們稱此模型（Y=Bo+B1X）為簡單線性迴歸分析。
迴歸分析是統計學上常被使用的一種分析方法，其主要在探討並建立兩變數間的直線關係，但若兩變數之間並非直線關係，而是具有其他非線性的函數關係時，我們又該如何處理呢？一般來說，我們可以直接將其中一個變數做數值的轉換，使轉換後的變數間可以呈現直線的關係，然後再進行線性迴歸分析；亦或是，我們在一開始建立資料間的數學模式時，即設定為非線性的關係，如倒數、指數等函數關係。
