迴歸分析是統計學上常用的分析方法,主要在建立一個函數(最能夠代表變數間的所有觀測資料),並用此函數來代表應變數和自變數之間的數學模式,以便觀察特定的變數來預測我們所感興趣的變數。若特定的變數(X)和有興趣的變數(Y)的數目都為一個,則我們稱此模型()為簡單線性迴歸分析。
另外要注意的是,建立迴歸分析前須檢查資料是否符合迴歸分析的三個假設-獨立、常態及均質。
範例中,我們使用SAS EG的範例資料CLASS。請選擇伺服器清單->伺服器->本機->資料館->SASHELP->CLASS
在工作的快捷選單中選擇分析->迴歸->線性迴歸
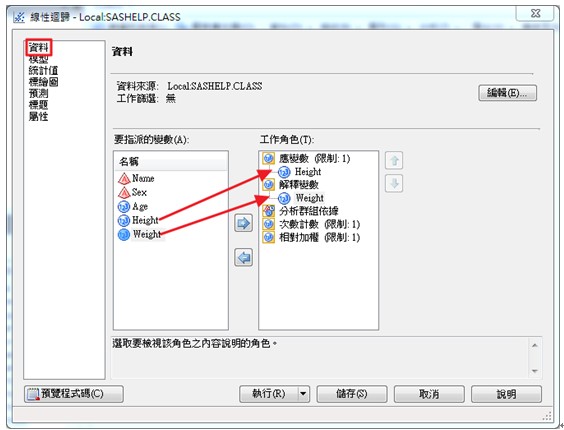
在左側的選單中選擇資料,將要指派的欄(A)中的Height和Weight兩變數,分別拖曳至右側工作角色(T)中的應變數及解釋變數的變數欄中。
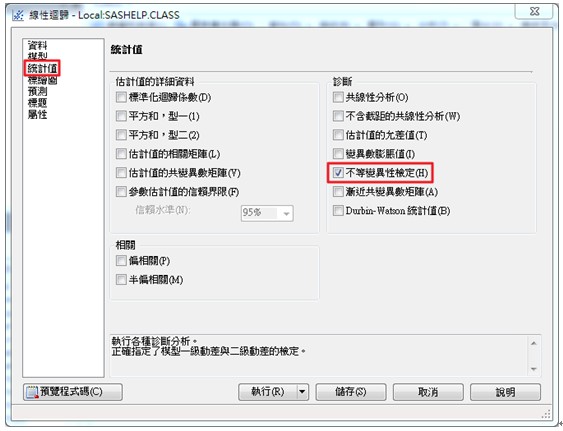
在左側的選單中選擇統計值,勾選不等變異性檢定(H)
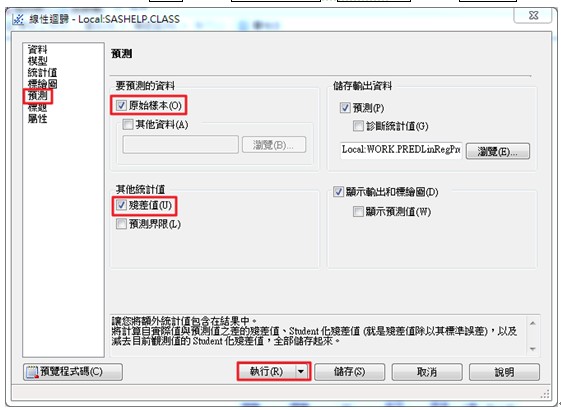
在左側的選單中選擇預測,勾選原始樣本(O)及殘差值(U),按下執行(R)。
進行迴歸分析前,我們要先檢測資料是否有滿足迴歸分析的3大假設-獨立、常態及均質。其中獨立的部分,應視分析者對資料的了解來判別資料間有無獨立。而常態的假設可以檢視殘差的圖形(直方圖、QQ-Plot、箱型圖) 或是利用其他統計方法(SW,KS,CV,AD)檢定殘差值來判別。均質的假設可以由殘差圖的檢視或是利用SAS的不等變異性檢定之。
以下我們對三個假設作進一步的說明。
- 均質性
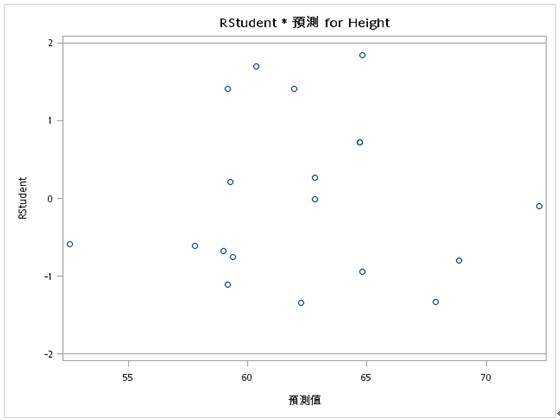
由SAS分析的結果圖表(RStudent*預測 for Height)中看出,殘差均勻分布在-2~2之間,故我們可以推論殘差具有均質性。
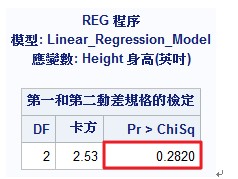
或者我們可以利用第一和第二動差規格的檢定來檢定殘差是否均質,由下表得知p-value=0.282 > ,在假設檢定中我們不拒絕,也就是我們沒有充份證據顯示該資料不具有均質性。故我們接受均質性的假設。
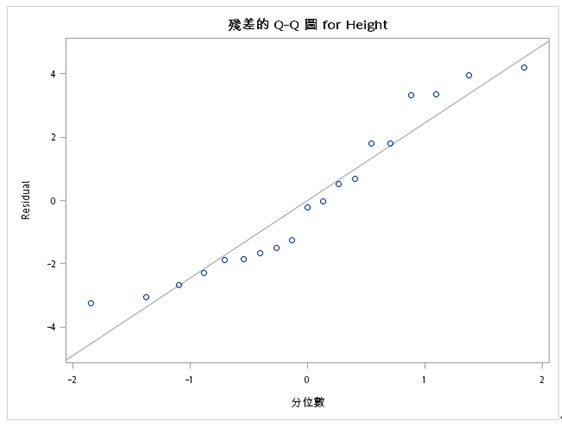
2. 常態性
由QQ-Plot圖中,看出殘差和常態分位數的分布,散落在45度的直線上。所以由此推斷殘差也具有常態性。
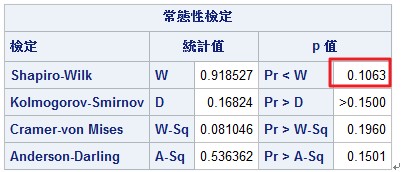
或者我們可以利用SAS的常態性檢定(Shapiro-Wilk)來檢定殘差。
在流程圖中點選SASHELP.CLASS 的線性迴歸預測及統計值
選擇描述->分配分析
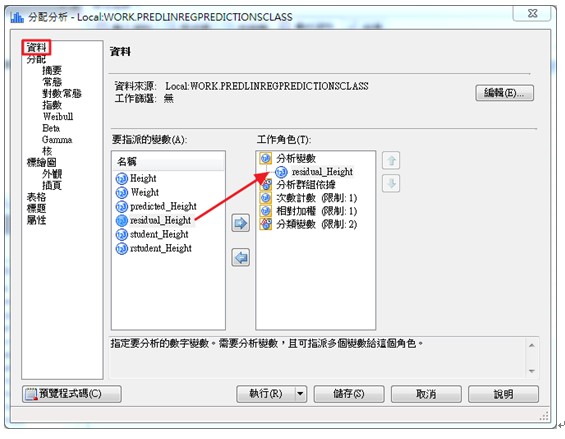
在左側的選單中選擇資料,將要指派的欄(A)中的residual_Height變數拖曳至右側工作角色(T)中的分析變數的變數欄中。
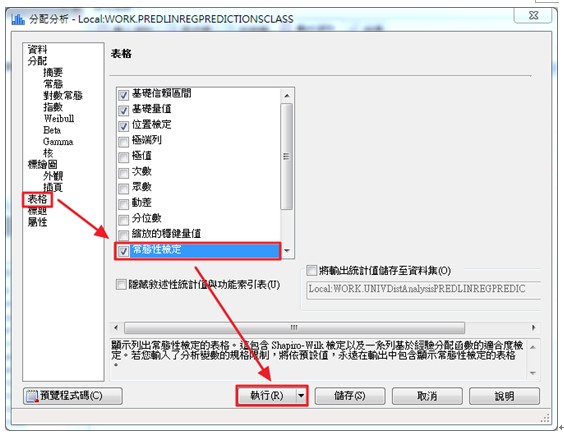
在左側的選單中選擇表格,勾選常態性檢定後選擇執行(R)。
由下表得知p-value=0.1063 > ,故在假設檢定中我們不拒絕Ho,也就是我們沒有充份證據顯示該資料不具有常態性。所以我們接受常態性的假設。
3.獨立性
本次分析沒有執行獨立性的檢定,因為作者認為該資料具有獨立性,並不需要利用統計分析證明之。
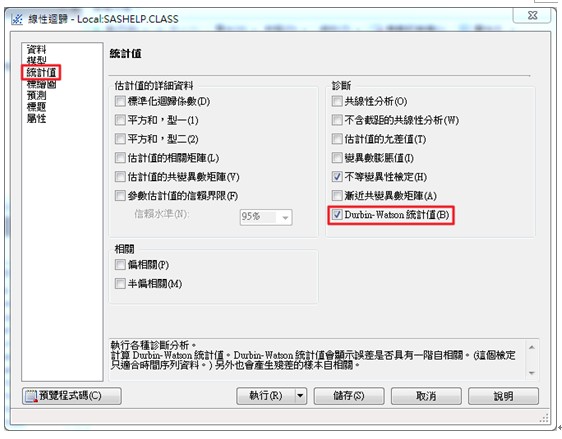
若是無法判定資料是否具獨立性而需藉由統計檢定輔助,我們可以在迴歸分析的步驟中,於左側的選單中選擇統計值,勾選Durbin-Watson統計值選項,即可獲得一階自我相關值來判定之。
Tags
