「混合模型」工作會讓各種混合線性模型符合資料，可讓您使用這些符合的模型對資料進行統計推論。

混合線性模型是標準線性模型的概括，概括的內容是允許資料呈現相關及非常數變異性。混合線性模型非常靈活，不僅可以建立資料平均值的模型，也可以建立其變異數與共變異數的模型。

另外在實驗設計中，因子可以分為固定效果跟隨機效果兩種，若是分析的模型中有隨機因子時，會造成部分因子的F值計算方式不同 (依據EMS Rules)，此時使用廣義線性模型來分析此資料時，所得的F值都是以MSE為分母，造成部分的因子檢定有錯誤。而我們必須另外使用test的語句來指定因子的F值計算方式以求得正確F值。若是使用混合模型，則我們只要正確指派變數角色，則EG就會得出正確的統計量。

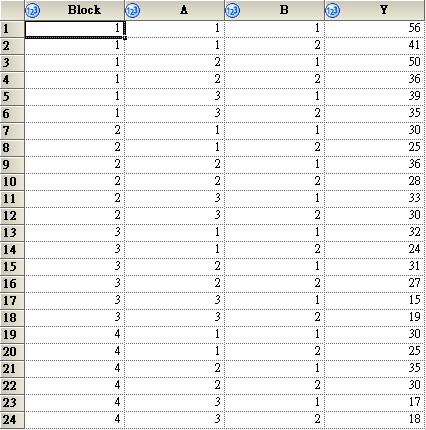
資料說明：

Y是我們的應變數，A和B都是實驗的固定效果因子而Block是隨機效果區集。以這個資料類型而言，若模型假設為Y=A+B+A*B+Block+A*Block。

依照EMS Rules，因子A的F=MS(A)/MS(A*Block)。

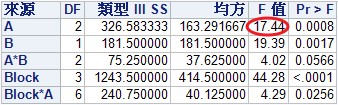
下表是利用廣義線性模型所得到的結果，其中A因子的F值為17.44。但是這個F值是以MSE為分母所得。

但是依照EMS Rules，其F值的計算方式應以MS(A*Block)為分母，所以我們要在廣義線性模型裡插入下列程式，表示A的分母是除以MS(A*Block)：

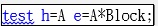
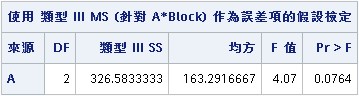
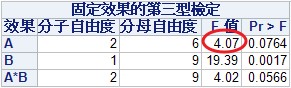
則在新執行的報表中會有下列新的報表產生，此時因子A的F值為4.07才是正確的F檢定統計量。

接下來，我們則使用EG的混合模型工作來幫我們快速達成上列的分析。

在工作的快捷選單中選擇【分析】→【ANOVA】→【混合模型】

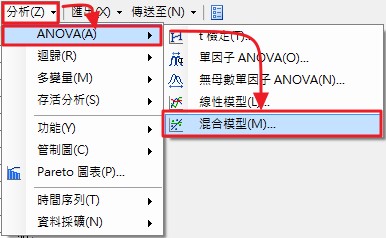
於左側的選單中選擇【資料】，將要指派的變數(A)中的【Y】變數，拖曳至右側工作角色(T)中的應變數欄；接著將要指派的變數(A)中的【A】、【B】和【Block】拖曳至右側工作角色(T)中的分類變數欄。

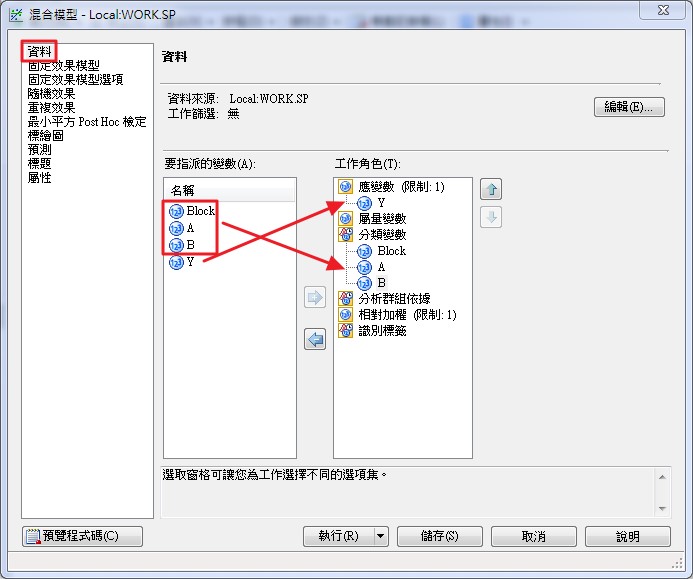
於左側的選單中選擇【固定效果模型】，先點選類別及屬量變數視窗中的【A】和【B】變數後，再點選【因子】按鈕，將A、B 和 A*B 加入右側的效果視窗。

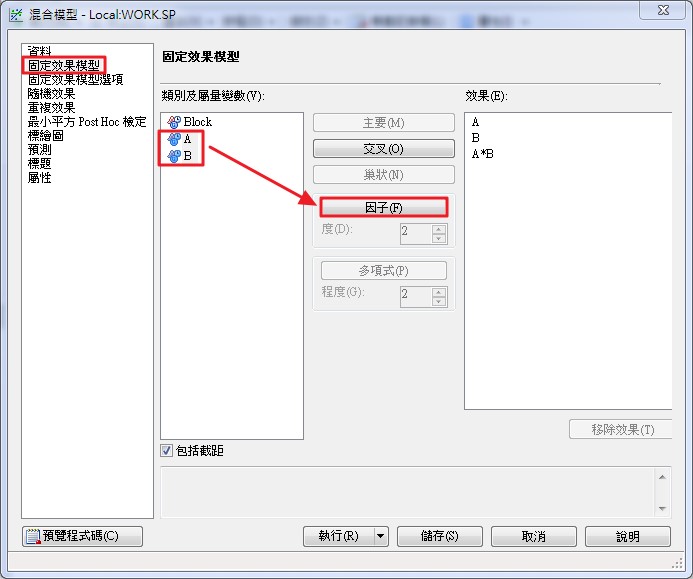
於左側的選單中選擇【隨機效果】，點選【增加】。

 在右側的隨機效果中點選，以選擇隨機效果變數進入模型。

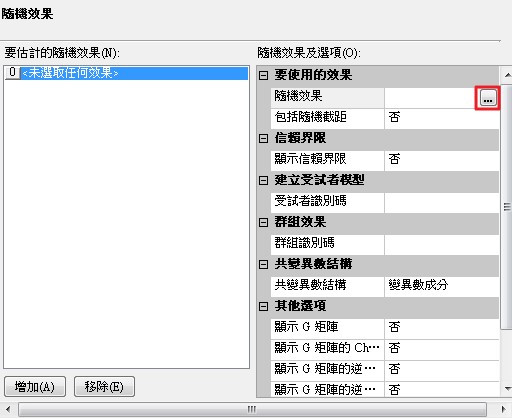
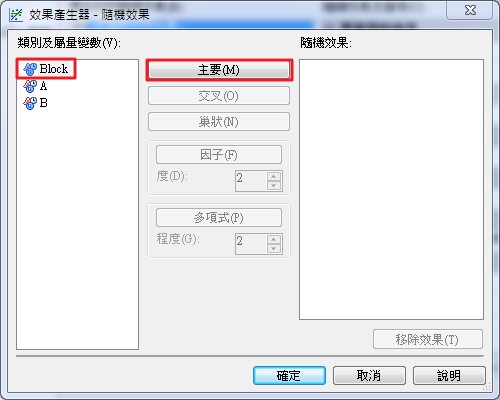
點選類別及屬量變數視窗中的【Block】變數後，再點選【主要】按鈕，將【Block】加入右側的隨機效果視窗。

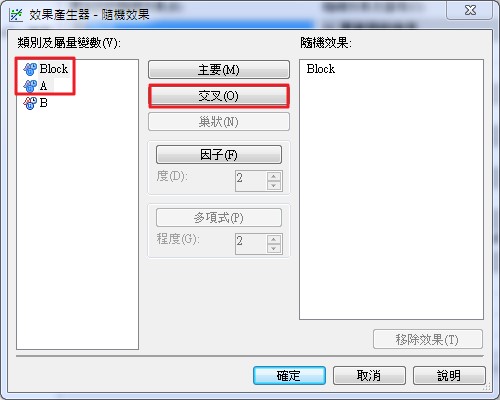
點選類別及屬量變數視窗中的【Block】和【A】變數後，再點選【交叉】按鈕，將【Block*A】加入右側的隨機效果視窗。

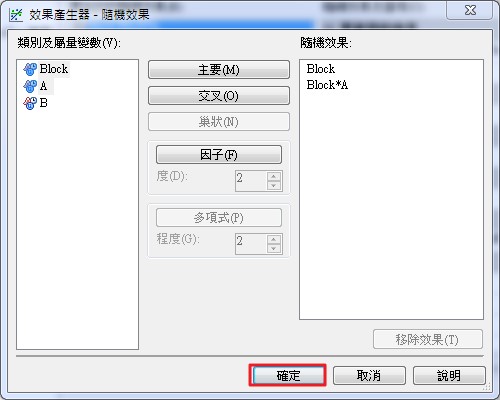
選擇【確定】。

選擇【執行】。

產生的結果如下：

下表中的A因子的F值是不是跟廣義線性模型中除上MS(A*Block)的F相等，這樣我們就不再需要先去利用EMS Rules求出F值的計算方法，也不用再以插入程式的方式求出正確的檢定統計量值。