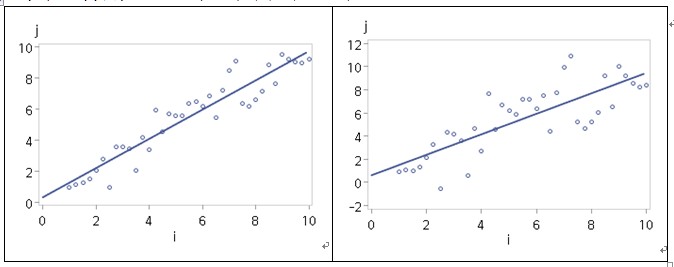
在做迴歸分析前,我們須先了解兩數值型變數間是否有呈現線性相關,最簡單的方式就是觀察兩變數的散佈圖。以下面兩張圖為例,雖然兩者均呈現線性相關,但相較於左圖而言,右圖的資料分布與迴歸線較為離散,所以我們可以因此而認定右圖資料不適合做迴歸分析嗎?也由於散佈圖的解說是很主觀的,如果我們只靠圖形來判別資料適不適合做迴歸分析,可能每個人的解讀結果都不相同。這時我們就需要有一個客觀的判斷準則--統計量。
由「共變異數」和「相關係數」兩個統計量可以看出兩個數值性變數之間的關係。其中,共變異數只能看出兩變數之間的正負相關性,而相關係數除了可以看出兩變數間的正負相關外,還可以看出兩者之間直線關係的強度。其相關係數的公式如下
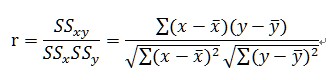
相關係數的意義:
- r的正負號代表著X與Y的相關性,如果r>0,表示X和Y為正相關,亦代表Y值會隨X值變大而增大;反之,如果r<0,表示X和Y為負相關,亦代表Y值會隨X值變大而縮小。
- |r|<=1。若|r|=1 則表示X和Y在一直線上,|r|越靠近1表示X和Y的直線關係越強;反之,若|r|越靠近0則表示X和Y的直線關係越弱。
相關係數的性質:
- 相關係數是一純量(scalar),具有單位不變性的性質
- 0<=|r|<=1
- |r|越靠近1表示X和Y的直線關係越強
- |r|表示表示X和Y的沒有直線關係,但不代表X和Y不具有其他的非直線關係
範例中,我們使用SAS EG的範例資料CLASS。請選擇伺服器清單->伺服器->本機->資料館->SASHELP->CLASS
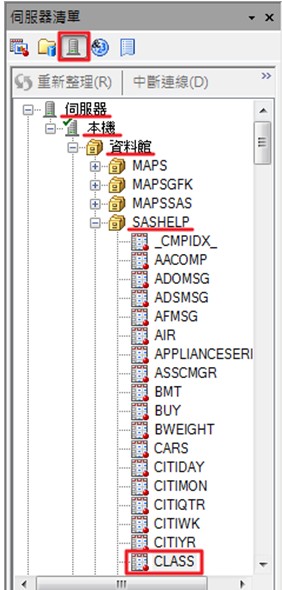
在工作的快捷選單中選擇分析->多變量->相關
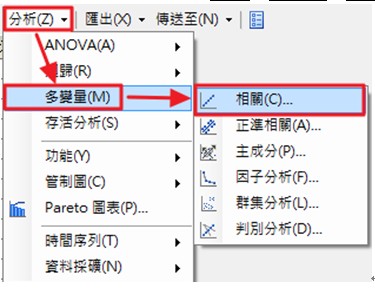
將要指派的欄(A)中的Height和Weight兩變數,分別拖曳至右側工作角色(T)中的分析變數欄後,選擇執行(R)。
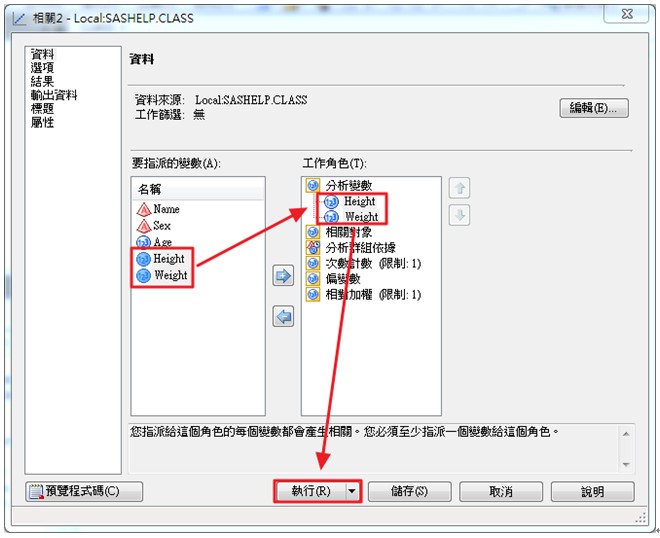
在SAS EG的結果裡會顯示出我們剛剛所執行的相關工作。
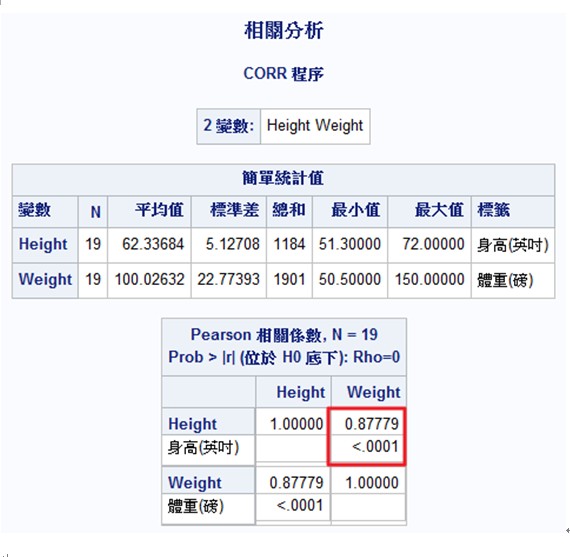
在上表中,除了可得兩變數基本的敘述統計量外,另由下方的Pearson相關係數表可得相關係數r=0.87779,可知兩變數間有高度的直線正相關。
另外,我們可由假設檢定的方法檢定之

結論:有充分證據顯示身高與體重有線性關係
如果Pearson相關係數表如下
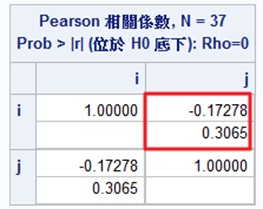
由相關係數r=-0.17278,可知兩變數間有低度的直線負相關,由假設檢定方法可得

結論:沒有充分證據顯示身高與體重有線性關係
Tags
