經過信度分析後,本單元要來教各位如何以因素分析來進行量表的項目分析
本篇文章Dr. SAS來教您 一 效度分析
本研究中「創新接受程度」、「產品創新屬性」、「消費者知識」與「購買意願」等四個量表,經過前述信度分析後,發現並沒有需要被刪除的問題。本單元將介紹如何以因素分析來進行量表的項目分析,而因素分析是用來研究量表建構效度(Construct Validity)的有效方法之ㄧ。
一、建構效度的意義
所謂的建構效度乃指研究量表可以有效的衡量出抽象概念的程度高低,可分為收斂效度(Convergent validity)與區別效度(Discriminant validity)兩項。當問題可以有效的被分配到一特定因素時,則具有收斂效度,在實務上,若問題的因素負荷量(Factor loading)絕對值在每個因素上都低於0.5時(也有學者取0.6作為標準),則表示該問題不具有收斂效度。當問題同時可以分配到2個以上的因素時,則該問題就不具有區別效度,在實務上,若問題的因素負荷量(Factor loading)絕對值在2個以上的因素都高於0.5時,則表示該問題不具有區別效度(也有學者以最大與最低因素負荷量數值差異在0.3以上做為標準)。如研究量表的所有問題同時具有收斂效度與區別效度時,則表示該研究量表具有建構效度。
二、因素分析的基本概念
因素分析為縮減構面的一種統計方法,其資料處理流程為由建立的資料矩陣中,求出問題(變數)X1,X2.....Xm. 與問題間的相關係數矩陣,問題間的相關係數越強,越有可能歸在同一因素內,相反的,問題間的相關係數越弱,則歸類在同一因素內的可能性就越低。其次,利用線性組合的方法來求出因素負荷量矩陣,並萃取出不同的因素F1,F2....Fp,因素負荷量的大小表示因素對問題的貢獻程度大小,此數值越大表示該因素因包含該問題。最後,由於我們要針對各因素來進行分析,也就是說原來的問題X1,X2....Xm已經縮減成F1,F2....Fp (m<p)的變數,因此,必須有一新產生的資料來取代原來輸入的資料矩陣,此資料即為因素分數矩陣;由於各因素對各問題的因素負荷量值不同,利用類似權重的概念,將因素負荷量矩陣轉換為因素分數矩陣。整個因素分析的基本概念如下圖所示:
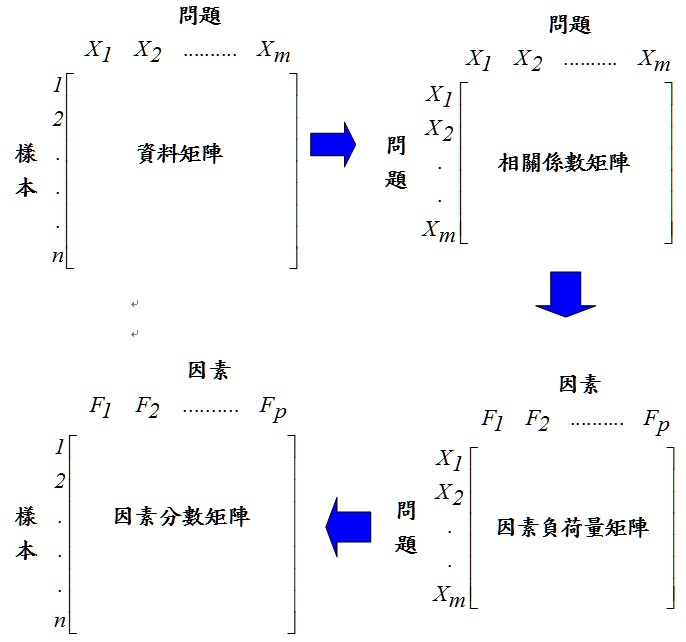
三、樣本的適切性
在因素分析中,通常都以Kaiser-Meyer-Olkin (KMO)做為指標來衡量是否適宜進行因素分析,其公式為
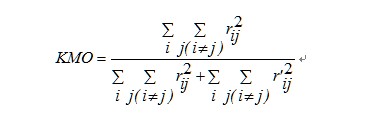
其中rij為表變數Xi和Xj的相關係數,表變數Xi和Xj的偏相關係數,KMO的值越小表示不適合進行因素分析,在實務上,通常要求KMO的值必須大於0.8。
四、因素個數的決定
1.特徵值大於1
這是最常用來決定因素分析中應萃取因素個數的方法,大部分的統計軟體,都是以此方法作為內設萃取因素個數的方法。觀察報表中,特徵值(eigenvalue)大於1者的個數作為應萃取因素的個數。但如果特徵值在1的臨界點附近時,可自行決定是否應增加應數個數,例如:有特徵值1.01與0.98,此兩個數值的差異很小,但依此方法時,特徵值為1.01者會被納入因素,但特徵值0.98者會被剔除於因素之外。由表3-1可以看出來,特徵值大於1者有4個,因此如採用此準則,則應萃取4個因素。
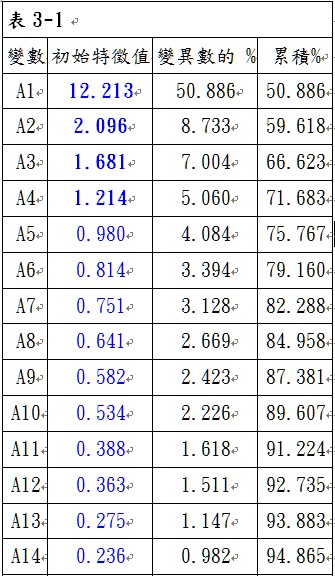
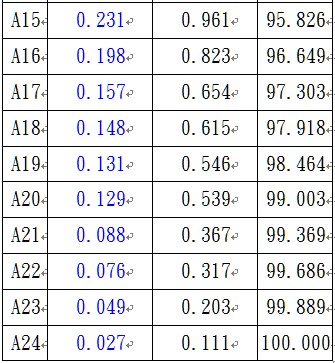
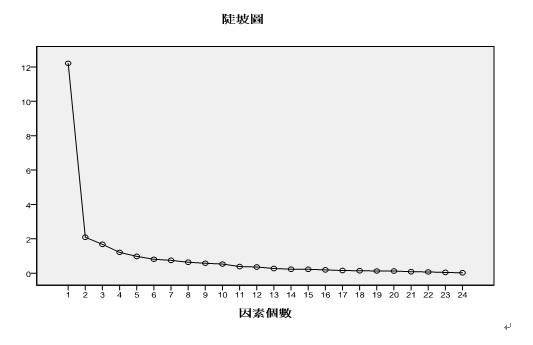
2.陡坡圖
此圖形乃是以因素個數為X軸,未轉軸前的特徵值為Y軸所畫出的散佈圖,由研究者主觀的由圖中自行判斷一臨界點,在此臨界點以上,特徵值的變動幅度大,但在此臨界點以下,特徵值的變動幅度小,此時,就以此臨界點所對應的因素個數最為萃取因素的數目。
五、共同性(Communality)
假設一量表有等m個問題,因素分析乃是將此m個變數分解成共同性因素(common factor)與獨特性因素(unique factor)的線性組合的一種方法,其模式如下:
其中
Fj:表第 j 個共同性因素(j=1,2,…..p)
aij:表共同性因素 Fj 的因素負荷量
P:表共同因素的個數。
Ui:表問題 Xi 之獨特性因素
bi:獨特性因素的因素負荷量。
吾人可以求得各問題的變異數分別為

所謂共同性乃指問題可以貢獻到因素的程度大小,其數值介於0至1之間,由上述的公式可以得知,當共同性越高時,該問題與共同因素的關係就越密切,獨特性就越低,則表示該問題對共同因素的貢獻就越大,所以就應該將該問題保留;一般建議,共同性的數值最好在0.5以上。例如:有一因素負荷量如下,其共同性的數值即為因素負荷量的平方和的加總:
| 表3-2 | |||
|
問題 |
因素負荷量 |
共同性 |
|
|
因素一 |
因素二 |
||
|
X1 |
-0.09349 |
0.88450 |
0.79108063 |
|
X2 |
-0.36996 |
-0.14011 |
0.156501213 |
|
X3 |
0.42366 |
0.68215 |
0.644816418 |
|
X4 |
0.84265 |
-0.29936 |
0.799675432 |
|
X5 |
0.73726 |
0.25298 |
0.607551188 |
|
X6 |
0.88700 |
0.07895 |
0.793002102 |
六、量表問題的進一步篩選
下面我們將針對「創新接受程度」、「產品創新屬性」、「消費者知識」與「購買意願」等四個量表,以主成分分析的估計方法,並以最大變異的轉軸方法來介紹如何一步一步的以收斂效度、區別效度與共同性的方法來進一步篩選量表的問題:
(1).「創新接受程度」量表
步驟1:
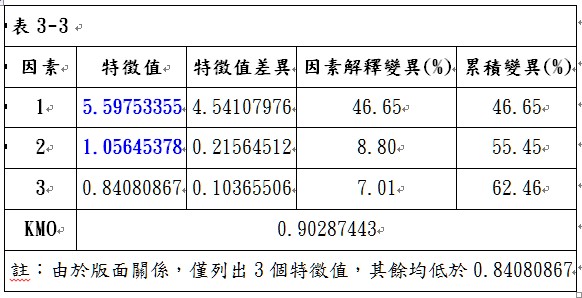
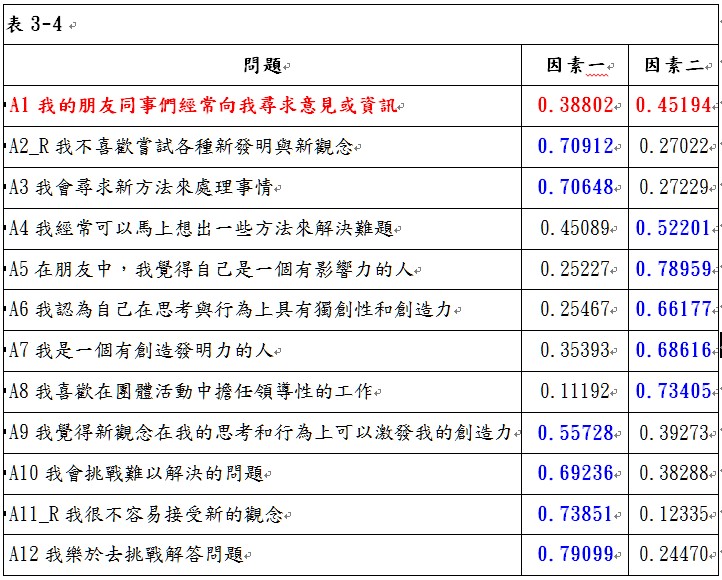
由原始的量表資料進行因素分析後,由表3-3可看出,KMO值為0.90287443,大於0.8,故可以進行因素分析。以特徵值大於1的個數做為萃取因素個數的準則,可以萃取2個因素,第1個因素可解釋46.65%的變異,第2個因素可解釋8.8%的變異,累積解釋變異為55.45%。轉軸後的兩因素的負荷量矩陣如表3-4所示,在表中可以看出,問題「A1我的朋友同事們經常向我尋求意見或資訊」在因素一與因素二的因素負荷量分別為0.38802與0.45194,都低於0.5,表示該問題不具有收斂效度,可加以刪除,刪除問題A1後再進行一次因素分析,進入步驟2。
步驟2:
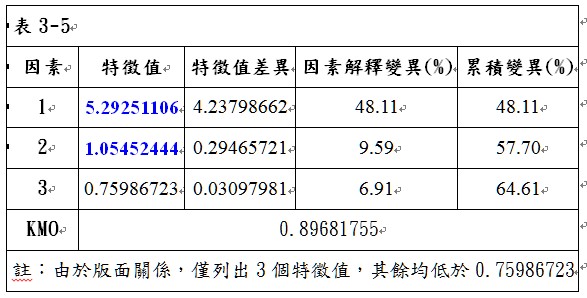
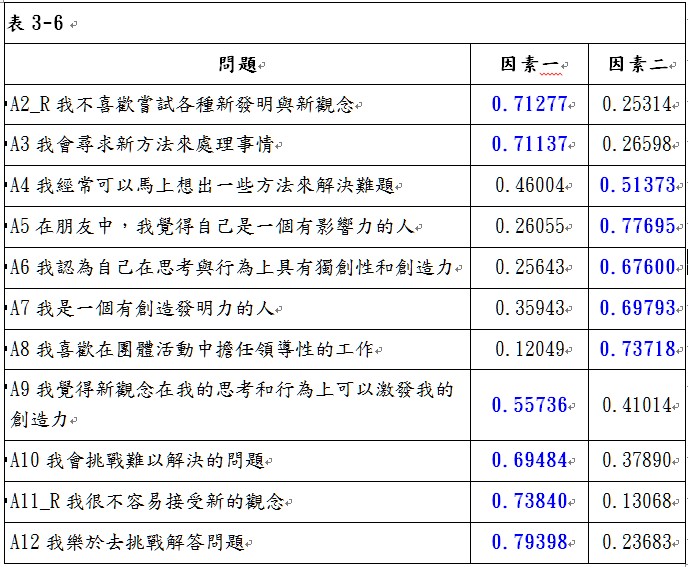
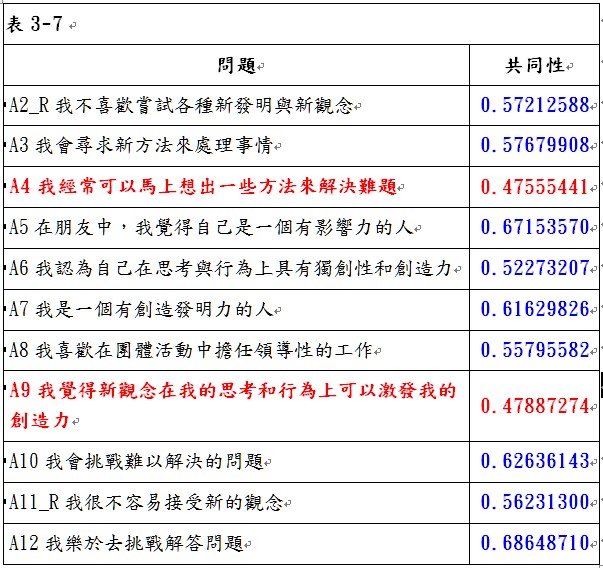
刪除問題A1後,由表3-5可看出,KMO值為0.89681755,大於0.8,故可以進行因素分析。以特徵值大於1的個數做為萃取因素個數的準則,可以萃取2個因素,第1個因素可解釋48.11%的變異,第2個因素可解釋9.59%的變異,累積解釋變異為57.7%。轉軸後兩因素的負荷量矩陣如表3-6所示,由表中可以看出,並沒有任何問題在因素一與因素二的因素負荷量低於0.5,表示這些問題具有收斂效度;同時,也沒有任何變數在因素一與因素二的因素負荷量同時大於0.5,表示這些問題具有區別效度。由於這些問題均具有收斂效度與區別效度,因此表示本研究量表具有建構效度。最後,必須再觀察這些問題的共同性是否夠高,由表3-7可看出,問題「A4我經常可以馬上想出一些方法來解決難題」與「A9我覺得新觀念在我的思考和行為上可以激發我的創造力」的共同性分別為0.47555441與0.47887274,均低於0.5;由於問題間都有相關存在,因此,不建議將兩個問題全部刪除,先刪除共同性最低的問題「A4我經常可以馬上想出一些方法來解決難題」,刪除問題A4後再進行一次因素分析,進入步驟3。
步驟3:
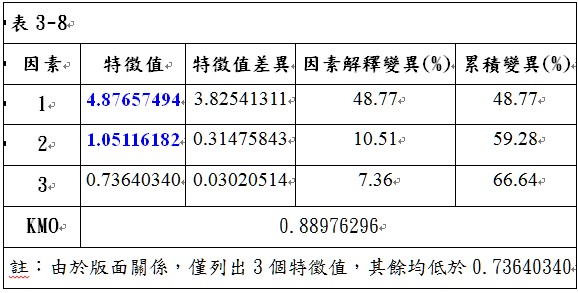
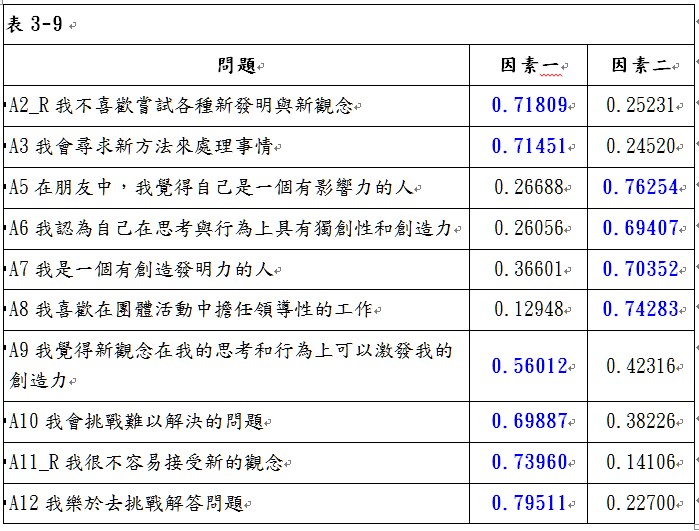
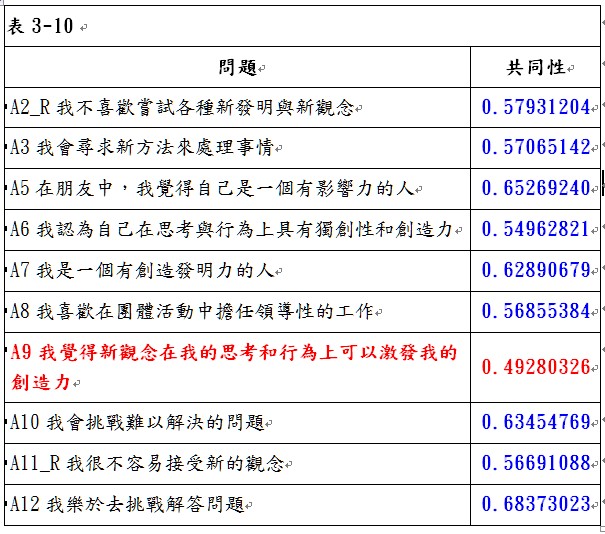
刪除問題A4後,由表3-8可看出,KMO值為0.88976296,大於0.8,故可以進行因素分析。以特徵值大於1的個數做為萃取因素個數的準則,可以萃取2個因素,第1個因素可解釋48.77%的變異,第2個因素可解釋10.51%的變異,累積解釋變異為59.28%。轉軸後兩因素的負荷量矩陣如表3-9所示,由表中可以看出,並沒有任何問題在因素一與因素二的因素負荷量低於0.5,表示這些問題具有收斂效度;同時,也沒有任何變數在因素一與因素二的因素負荷量同時大於0.5,表示這些問題具有區別效度。由於這些問題均具有收斂效度與區別效度,因此表示本研究量表具有建構效度。同時,必須再觀察這些問題的共同性是否夠高,由表3-10可看出,問題「A9我覺得新觀念在我的思考和行為上可以激發我的創造力」的共同性為0.49280326,低於0.5,因此,刪除問題「A9我覺得新觀念在我的思考和行為上可以激發我的創造力」,刪除問題A9後再進行一次因素分析,進入步驟4。
步驟4:
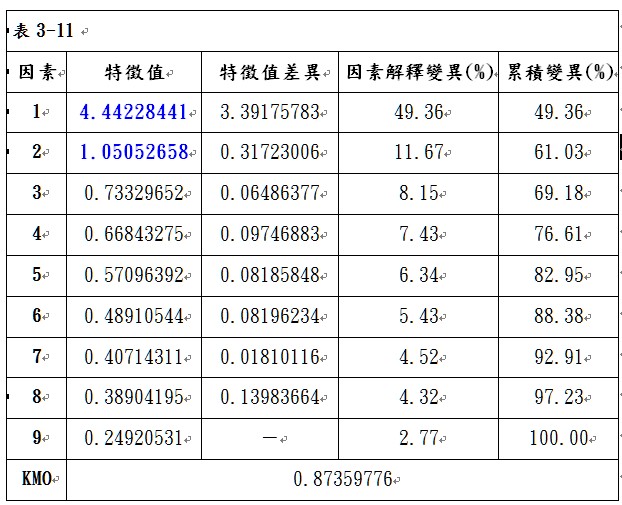
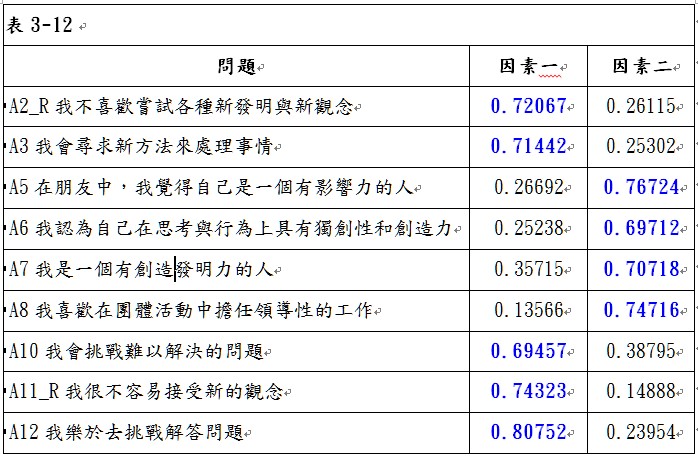
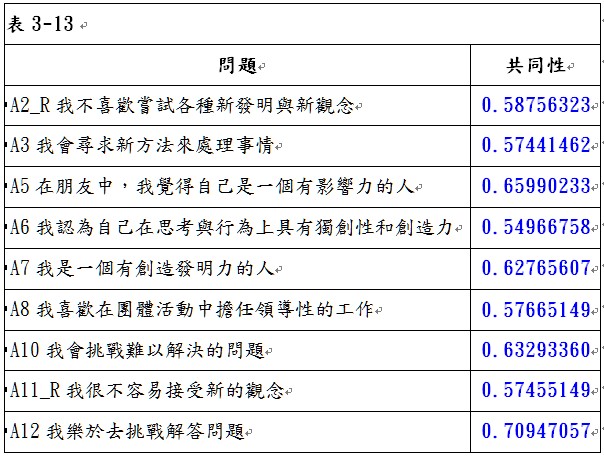
刪除問題A9後,由表3-11可看出,KMO值為0.87359776,大於0.8,故可以進行因素分析。以特徵值大於1的個數做為萃取因素個數的準則,可以萃取2個因素,第1個因素可解釋49.36%的變異,第2個因素可解釋11.67%的變異,累積解釋變異為61.03%。轉軸後兩因素的負荷量矩陣如表3-12所示,由表中可以看出,並沒有任何問題在因素一與因素二的因素負荷量低於0.5,表示這些問題具有收斂效度;同時,也沒有任何變數在因素一與因素二的因素負荷量同時大於0.5,表示這些問題具有區別效度。由於這些問題均具有收斂效度與區別效度,因此表示本研究量表具有建構效度。但最後必須再觀察這些問題的共同性是否夠高,由表3-13可看出,所有問題的共同性均高於0.5,因此,就完成了以因素分析來進行建構效度分析的過程,由表3-11可以看出因素一包含了問題「A2_R我不喜歡嘗試各種新發明與新觀念」、「A3我會尋求新方法來處理事情」、「A10我會挑戰難以解決的問題」、「A11_R我很不容易接受新的觀念」與「A12我樂於去挑戰解答問題」等5個問題,可解釋49.36%的變異;因素二包含了「A5在朋友中,我覺得自己是一個有影響力的人」、「A6我認為自己在思考與行為上具有獨創性和創造力」、「A7我是一個有創造發明力的人」與「A8我喜歡在團體活動中擔任領導性的工作」等4個問題,可解釋11.67%的變異,兩因素累積解釋變異為61.03%。將剩餘的9個問題重新進行總量表的信度分析與2個分量表(2個因素)的信度分析,進入步驟5。
待續。。。。。
Tags
