根據【系列3-1】實戰演練所整理好的資料集或跟著【系列3-2 製作圖表】接續來執行統計分析。
點選資料集上方選單【處理流程】即可回到流程圖
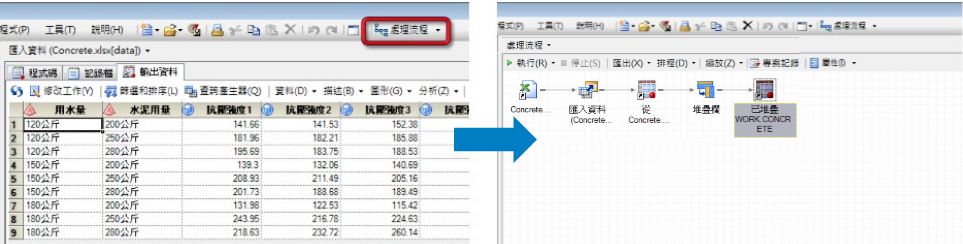
線性模型
回到流程圖中選擇【已堆疊】資料→點選工具列【工作】→【ANOVA(A)】→【線性模型(L)】
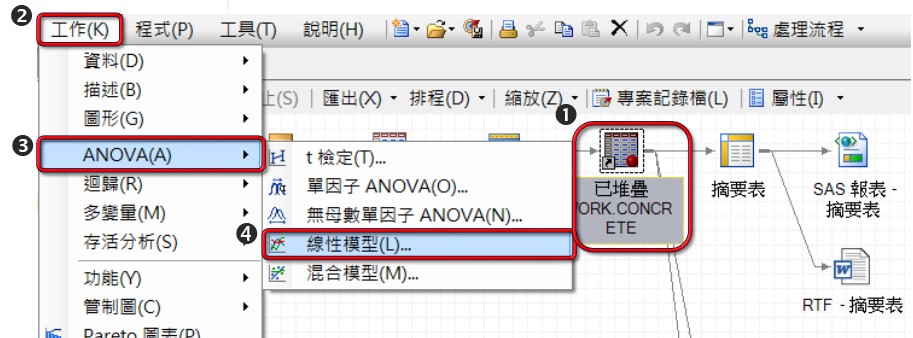
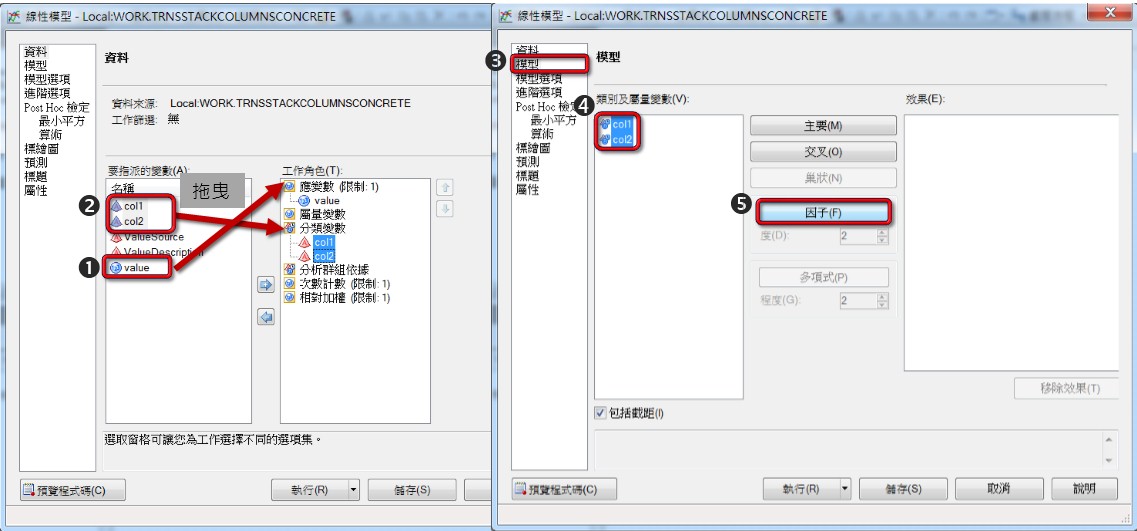
將col1與col2拖曳至【分類變數】,value拖曳至【應變數】
左側工作設定的【模型】→點選【col1與col2】→【因子】。
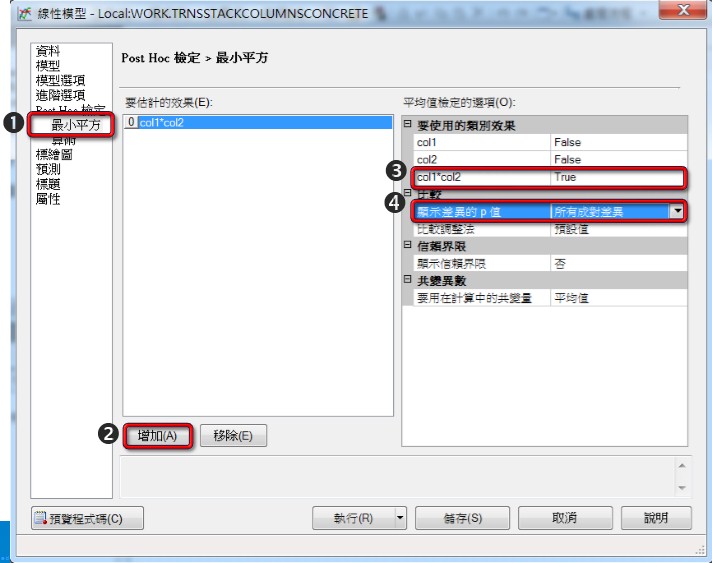
左側工作設定的【最小平方】→點選【增加】→【col1*col2】→選擇比較【所有成對差異】。
左側工作設定的【標繪圖】→勾選【自訂標繪圖清單】→勾選【交互作用】,左側工作設定的【預測】
→勾選【原始樣本】→勾選【殘差圖】後點選【執行】。
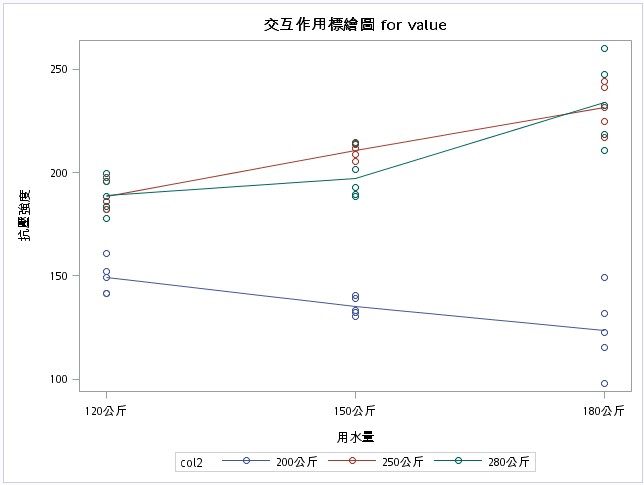
首先,使用變異數分析資料前,先檢視用水量與水泥用量間是否存在交互作用。
由左圖可知,當用水量與水泥用量所得到的交互作用圖,其直線有交叉,表示不同的用水量與水泥用量,其抗壓強度會互相影響。
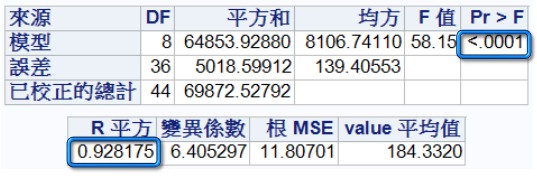
p值可知此模型的迴歸係數至少有一不為0,所以用水量、水泥用量與兩者交互作用,
至少有一對抗壓強度有影響;由此模型,用水量、水泥用量與兩者交互作用對抗壓強度的解釋能力有93%。
至少有一對抗壓強度有影響;由此模型,用水量、水泥用量與兩者交互作用對抗壓強度的解釋能力有93%。
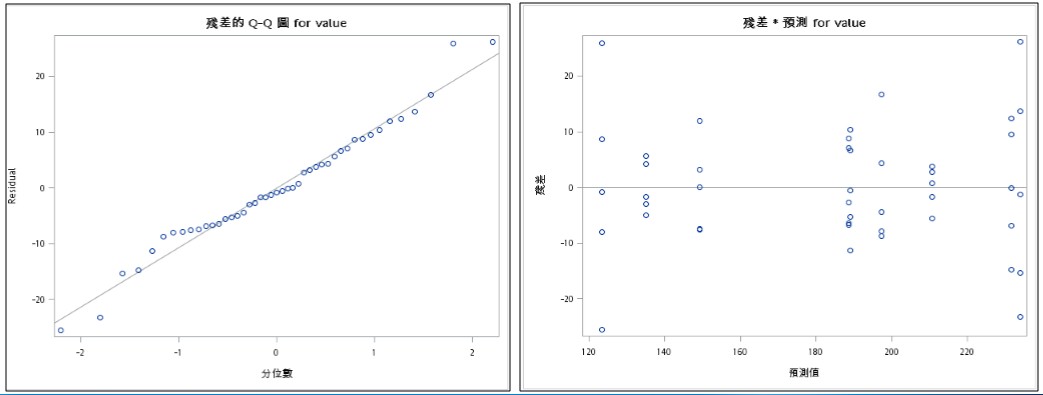
變異數分析須符合常態性、同質性與獨立性,由右圖沒有明顯趨勢可知此模型的殘差符合同質性;
由下圖殘差與參考線非常接近可知此模型符合常態性。
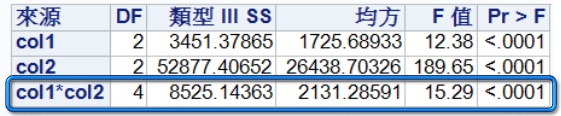
下表p值可知,用水量對於抗壓強度的影響,也會隨著水泥用量而改變,兩者的交互作用存在。
因此,可進行多重比較,找出用水量與水泥用量在何種組合下,會有較佳抗壓強度。
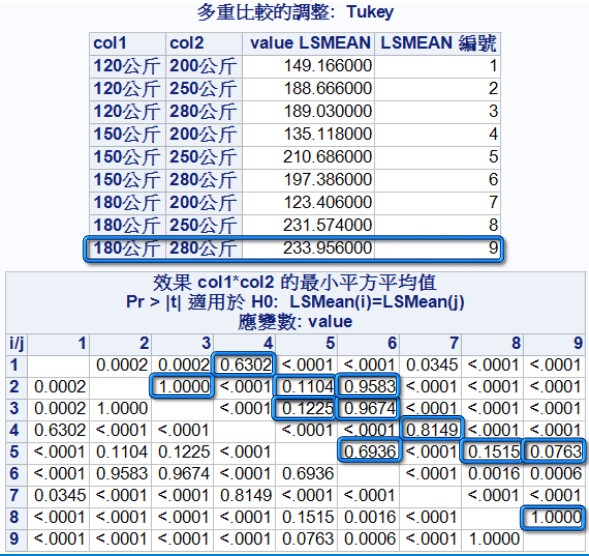
由下表可知,第1組與第4組、第2組與第3組…等水泥抗壓強度沒有顯著差異。
此外,第9組的水泥抗壓強度最高,且與第8組沒有明顯差異。
因此,用水量為180公斤且水泥用量為250與280公斤時,為最佳抗壓強度的組合。
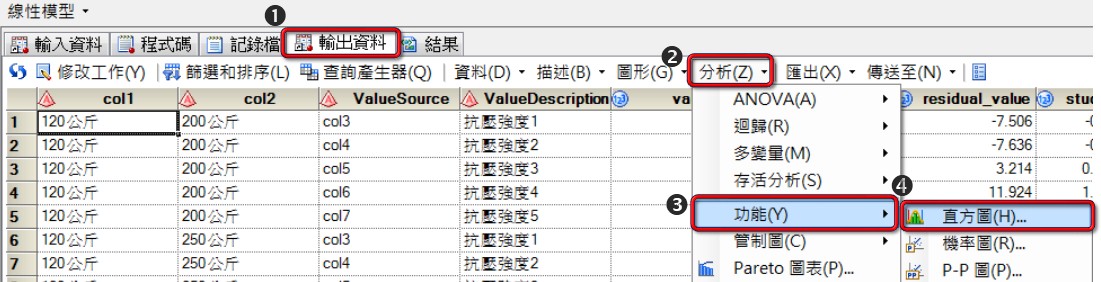
變異數分析(檢驗常態性)
點選【輸出資料】→點選快捷選單中的【分析】→【功能】→【直方圖】。
將變數residual_value拖曳至【分析變數】,點選左側工作設定的【常態】→將【常態】勾選後點選【執行】。
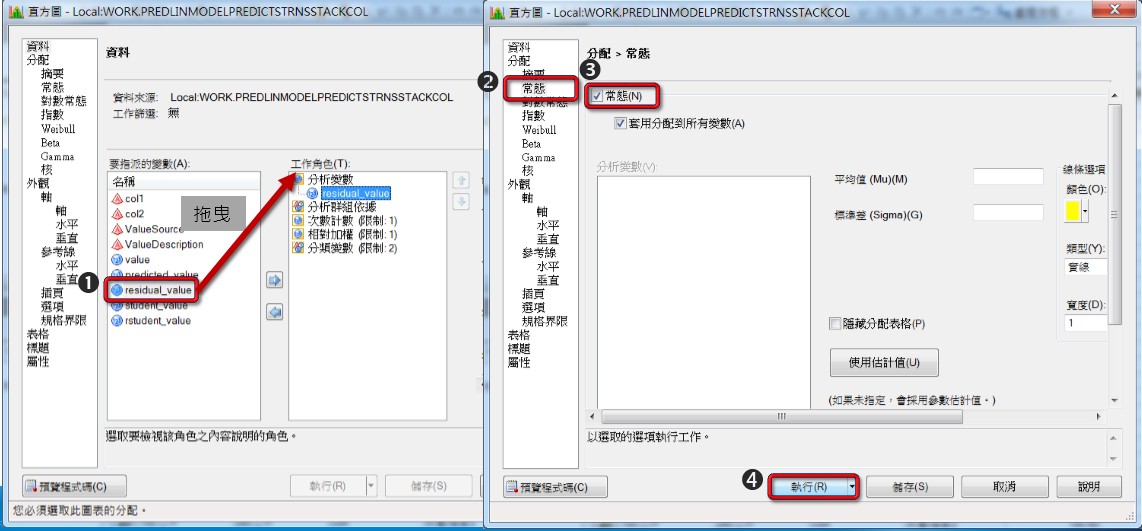
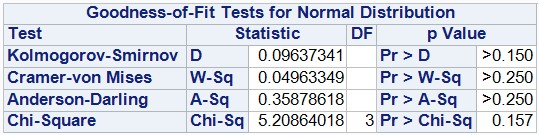
前面使用圖形可看出殘差沒有違背常態性,在此可由檢定方式得到殘差的確符合常態分配。
合併報表
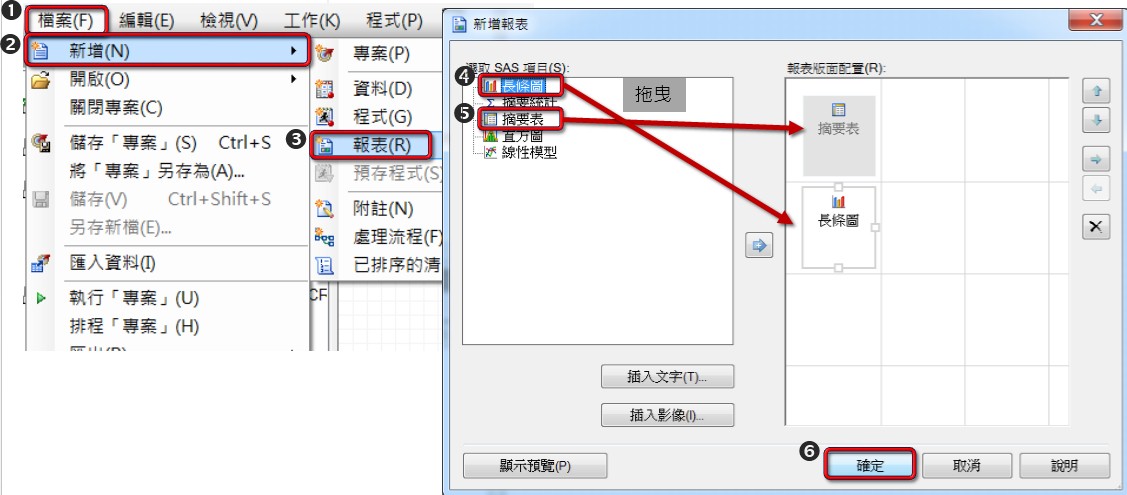
點選【檔案】→【新增】→【報表】,將把想合併的報表拖曳至相對位置,按【確定】後即完成合併。
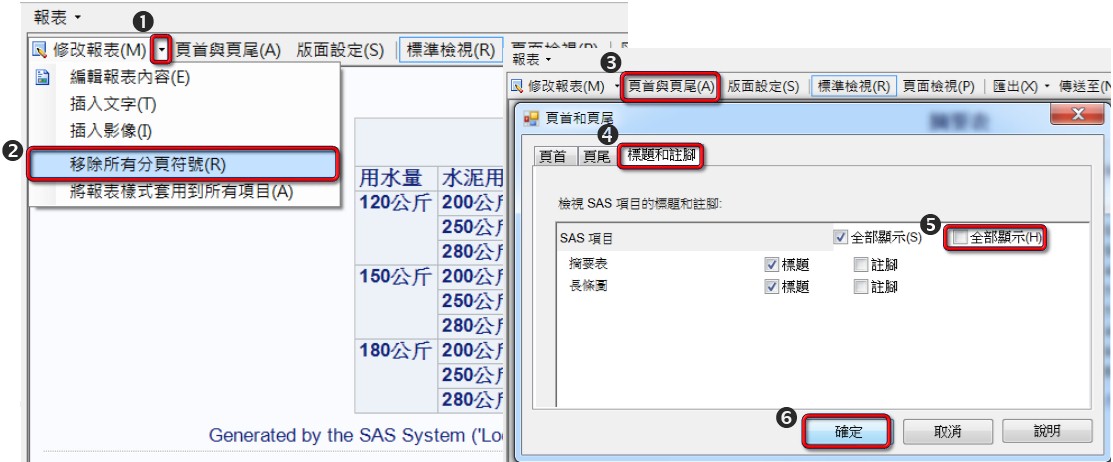
在快捷選單的【修改報表】中可【移除所有分頁符號(R)】,於快捷選單【頁首與頁尾】可修改【標題和駐腳】,設定完後按【確定】來完成。
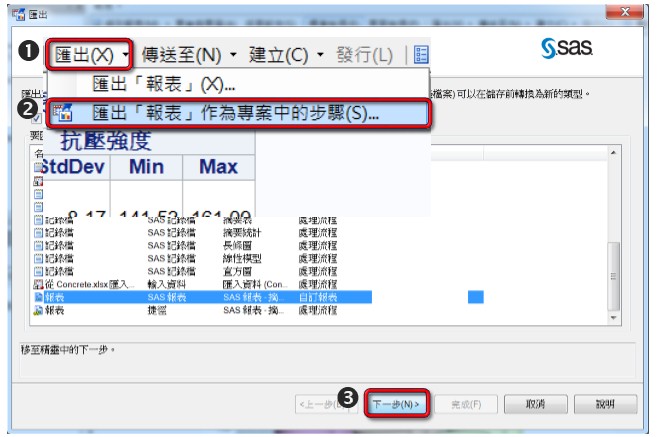
若想匯出報表,請點選快捷選單中的【匯出(X)】 →【匯出「報表」作為專案中的步驟(S)…】→【下一步】。
選擇【輸出檔類型】→點選【瀏覽】可更改儲存位置→【儲存】→【下一步】→點選【完成】後即輸出至您所儲存的位置。
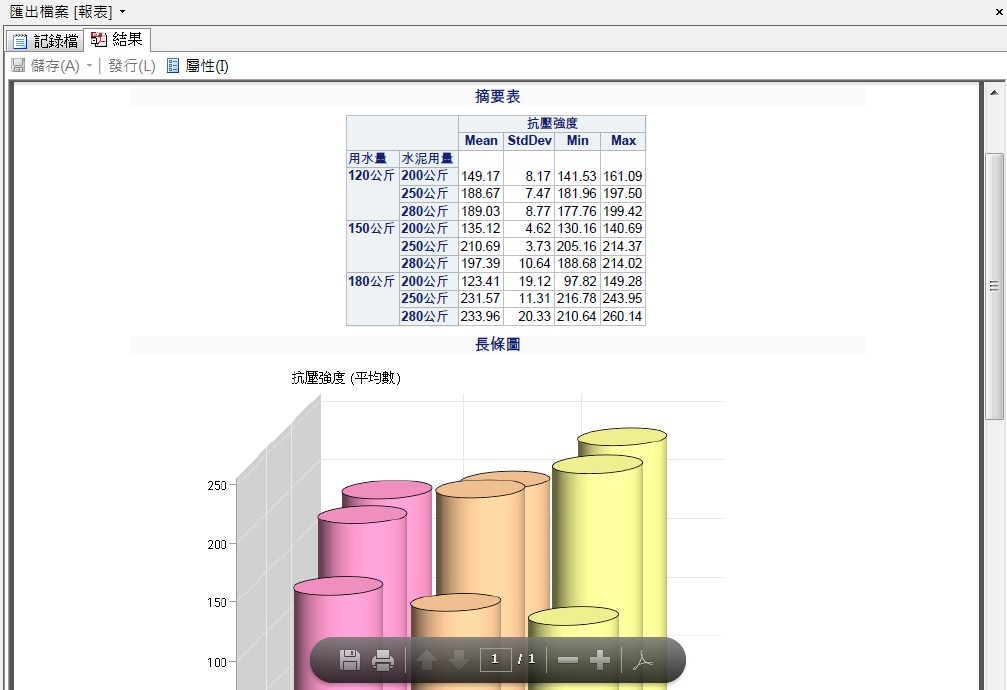
即合併報表結果如下:
結論
水泥實驗數據用表格與圖形呈現?
用水量與水泥用量何種組合有最佳抗壓強度?
●從前面表格與圖形可知:
用水量180水泥用量280,水泥抗壓強度較高用水量150水泥用量250,
水泥抗壓強度資料較集中不論何種用水量下,水泥用量250及280時,其抗壓強度較大。
●從前面變異數分析結果可知:
模型符合常態性、獨立性、同質性模型解釋能力達93%模型有交互作用,用水量對於抗壓強度的影響,
也會隨著水泥用量而改變用水量180且水泥用量250與280時,為最佳抗壓強度的組合。
<<完>>
Tags
