迴歸模型 (Linear Regression Model) 是非常流行的統計模式,分析的結果也被大量地應用在各個產業上,然而,迴歸分析雖也屬於資料探勘裡常用的演算方法,但它主要的演算方法卻是來自於統計分析的推估,因此須在正式進入迴歸分析之前,必須先確認各項資料條件滿足迴歸模型的基本假設,才適宜選用迴歸模式進行分析。否則,會造成資料本身不配適迴歸,但卻強迫進行迴歸模型建置,最終結果會造成模型解釋力始終無法被提升。
迴歸模式為一分析依變數(Dependent variable,EM又稱目標變數)與自變數群(Independent variable,EM又稱投入變數)間的線性關係之統計模式,故又稱線性迴歸模式(Linear Regression Model)。線性迴歸模式因底層的演算方法,投入變數以數值型態資料為佳,然而在社會科學問題裡,可能影響目標變項的分析變項則多屬於類別性非連續的資料型態。因此,對於研究變項屬於分類問題時,線性迴歸就不適用了。然而,多數的分析研究,往往直接進行主題研究的迴歸分析結果,卻忽略了資料本身可以一開始就不配適迴歸分析,錯誤分析方法的選擇往往會導致錯誤的解釋結果產出。
因此,本期專欄Dr.SAS將要介紹如何運用SAS工具平台,透過 EM來進行最適的迴歸分析方法的正確流程,以及當觀測資料不滿足迴歸分析的模型假設時,如何透過適當地資料的轉置與處理,讓分析者一樣可以選擇迴歸分析來產出預測規則與結果。
什麼是迴歸分析
迴歸分析為一建立變數間線性方程式之統計程序,透由統計方法建立依變數為自變數的函數模型,透過迴歸預測式來解釋資料過去的現象,並進一步對於一組新的觀測資料,產生可能的預測結果。
迴歸分析依照目標變數的資料型態,分為一般線性迴歸與羅吉斯迴歸分析 (Logistic Regression)。如果只有一個預測變數,則稱之為簡單迴歸分析。若有二個以上預測變數,則稱為多元迴歸或複迴歸分析。一般線型迴歸模式的表示式如下:
Y= W0+ W1X1 + W2X2 + …… .+ WmXm + ε
其中,W0為迴歸截距項與Wi為迴歸係數(j=1, 2, ……, m),ε為模型誤差項。各項係數參數估計則是透過最小平方估計式(OLS)來估計,最小平方估計追求的即是模型誤差的最小化,各觀測資料與預測迴歸式間的誤差距離平方和最小為目標式,進行預測迴歸式的各項參數係數的估算。
當目標變數為類別型資料型態時(二元資料型態如:是或否、回應或不回應、同意或不同意),此時則適用羅吉斯迴歸分析。羅吉斯迴歸類似線性迴歸模式,預測值Y為經過log函數轉換,轉換後的值才與投入變數間呈現線性關係。羅吉斯迴歸模型的表示式如下:
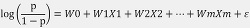
其中 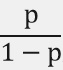 稱為勝算比 (Odds Value) , p為事件發生的機率值
稱為勝算比 (Odds Value) , p為事件發生的機率值
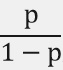 稱為勝算比 (Odds Value) , p為事件發生的機率值
稱為勝算比 (Odds Value) , p為事件發生的機率值羅吉斯迴歸透過Log函數轉換產生了一個臨界遞增的 S 型函數,適用於分析機率模型。邏輯斯迴歸分析的的各項參數係數,則是透過最大概似法(MLE)進行估計。
迴歸模式的基本假設
在正式進入迴歸分析之前,則應檢視資料是否滿足迴歸模式的基本假設,才適宜選擇迴歸分析方法:
- 常態性與變異同質性
(normality and equality of variance) - 殘差獨立性(independence)
每個殘差彼此之間是統計獨立的,觀察值之間彼此不會互相影響,若違反此假設,估計量會缺乏效率性。
- 直線性(linearity)
即所有抽樣樣本分配的平均數 (μY/X) 均落在母群迴歸線上
- ei~N〔 0 ,1 〕
誤差其分配服從平均數為0,變異數為1的常態分配,且各誤差項間彼此獨立
檢視上述基本假設的滿足性,最基本的資料瀏覽方式則可透過EM工具 Explore頁籤下的Graph Explorer節點選取散布圖(scatter plot),是否大致符合線型模式趨勢。
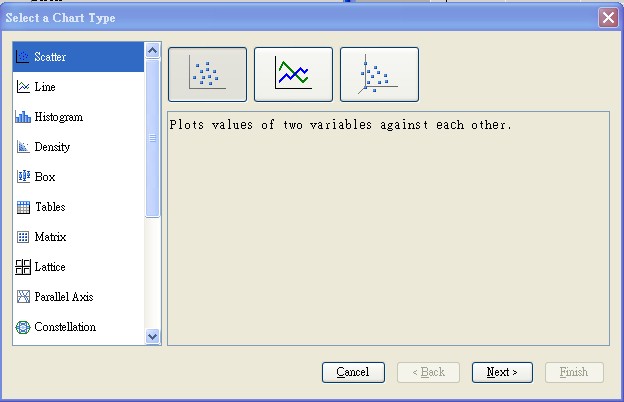
圖一、SAS EM-Graph Explore節點—散布圖
檢驗資料是否滿足迴歸假設的方法,Dr.SAS更建議讀者可以使用SAS EG下工作程序下Describe>> Distribution Analysis,選擇Normal Distribution來進行檢驗,EG提供各種詳盡統計量來協助分析者判讀資料的常態性。EM所提供的迴歸分析是以資料探勘的觀點,所以主要目的在於建置預測模型,不在於資料的檢定,因此相關的資料檢定或分析瀏覽的工作程序建議可以整合SAS EG進行對應的處理工作。
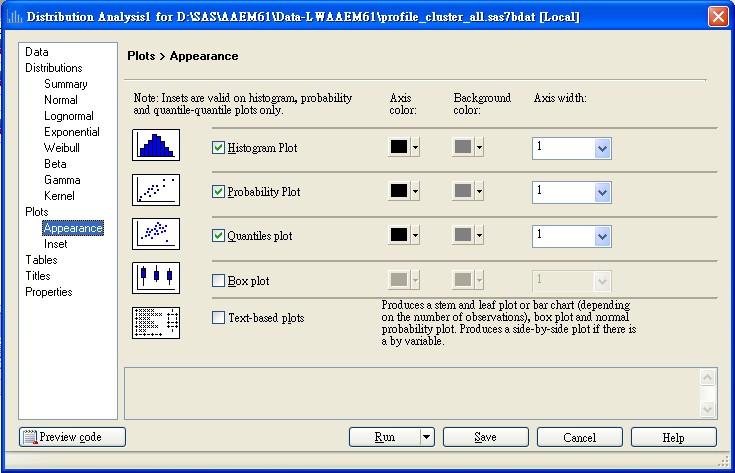
圖二、SAS EG-Distribution Analysis
若讀者們想要將EG的迴歸分析前置的檢定工作移植到EM上,可將EG工作程序產出的SAS程式碼複製到EM工具下Utility頁籤下的SAS Code節點的程式編輯區裡儲存並執行。如此,迴歸檢定工作就可以和迴歸分析建模做整合。
(下期繼續介紹EM迴歸分析最佳實務分析流程)
Tags
