在多變量分析中，主成分分析（Principal components analysis, PCA）是一種分析、簡化數據集的技術。利用原有的變數組合成新的變數，以達到資料縮減的目的，但卻能夠保留住數據本身所提供的重要資訊。由於主成分分析主要依賴數據提供的訊息，所以數據的準確性對分析結果影響很大。

資料說明：

此例中的資料是選定某些城市在一月和七月的日平均氣溫。主要用來說明主成分分析是如何將原始變量做正交旋轉成新的變數。

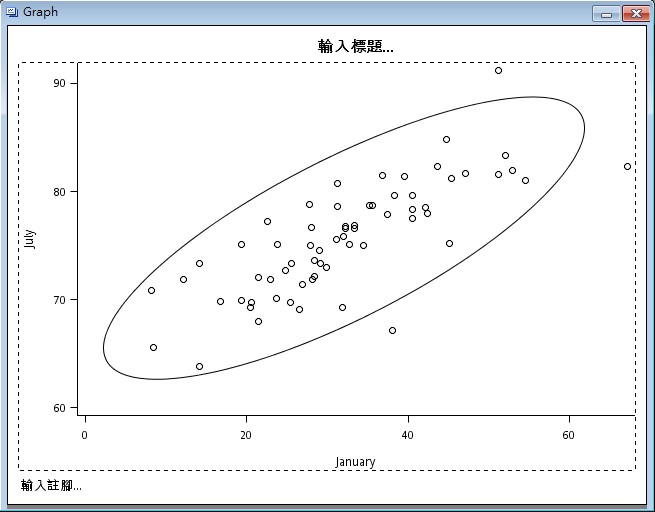
下圖是資料中一月和七月的日平均氣溫所繪製的散佈圖，由圖中可觀察到各城市一月和七月之日均溫的關係。

在工作的快捷選單中選擇<分析>→<多變量>→<主成分(P)>

於左側的選單中選擇<資料>，將要指派的變數(A)中的和變數拖曳至右側工作角色(T)中的分析變數欄中

在左側的選單中選擇<分析>，在分析(A)中選擇<共變異數>。

在左側的選單中選擇<標繪圖>，勾選<建立主成分計分的散佈圖(M)>及<建立模型成分圖(C)>選項，按一下<執行>

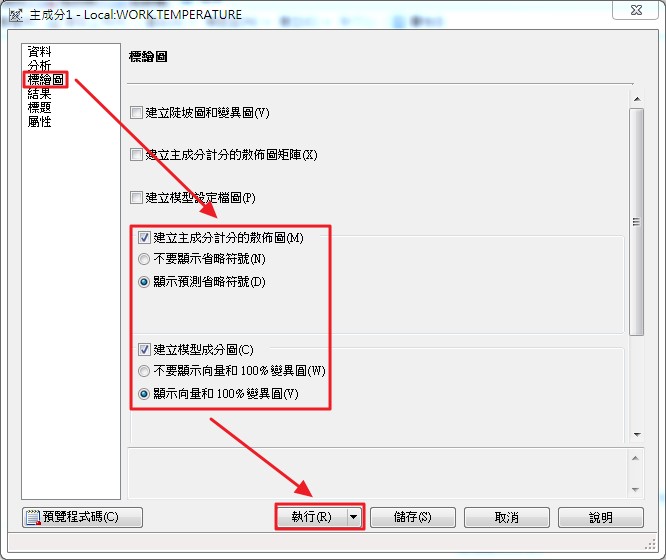
結果如下表所示：

總變異數為163.474，其中第一主成分解釋了約94％的總變異，而第二主成分解釋的變異約只有6％。在特徵向量表中，PRIN1中一月(January)所占的比例比較高，因為一月的資料比七月的資料有更高的標準差(Std)11.7124。

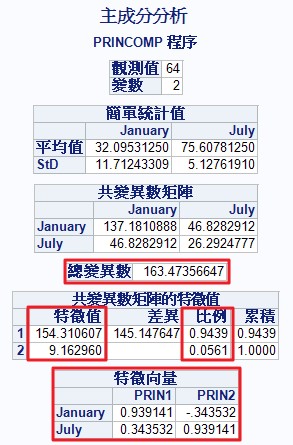
由模型成分圖可以看出原始變數和對應的主成分變數之間的關係。

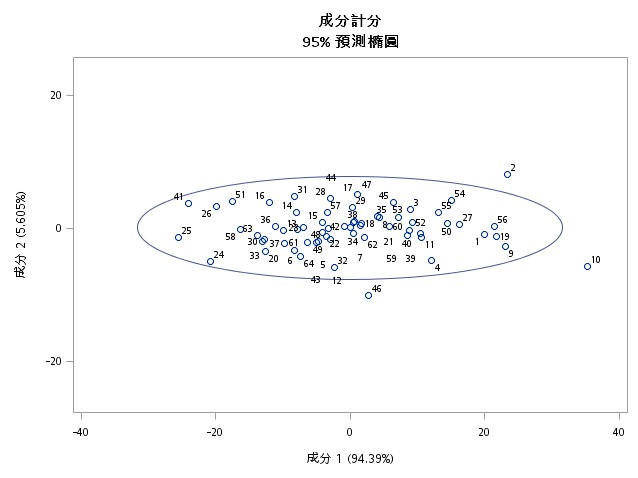
由成分計分圖中可看出主成分是原始變量的和，第一主成分具有比所述第二主成分較大的方差正交旋轉。

實際上，第一主成分比各自原始變量(七月和一月)有較大的變異。另外，我們可觀察到落在橢圓外的3筆資料為可能的離群值。