Lo que llamamos azar es nuestra ignorancia de la compleja maquinaria de la casualidad...
Jorge Luis Borges
Los éxitos de la ciencia en su alianza con la tecnología son indudables. Nos han proporcionado una gran capacidad para explicar, controlar y transformar el mundo.
La importancia de la ciencia y la tecnología aumenta en la medida en la que el mundo se adentra en lo que se ha dado en llamar "la sociedad del conocimiento".
Es así, como en esta entrega del “Sommelier del riesgo” hablaremos de dos técnicas analíticas que, combinadas con la tecnología, son de suma utilidad. Estos métodos matemáticos son la “Simulación de Monte Carlo” y el “Análisis bayesiano”.
Pasemos a hablar de los mismos…
Simulación Monte Carlo:
El nombre y el desarrollo sistemático del método de Monte Carlo data aproximadamente de 1944. Se entiende por tal al sistema en el cual se generan números de forma aleatoria pero condicionado a que los datos resultantes sigan un cierto patrón estadístico de comportamiento.
La clave de este método está en entender el término “simulación”. Realizar una simulación consiste en repetir las características y comportamientos de un sistema real. Así pues, el objetivo principal de la simulación de Monte Carlo es intentar imitar el comportamiento de variables reales para, en la medida de lo posible, analizar o predecir cómo van a evolucionar.
El método fue llamado así por el principado de Mónaco por ser ``la capital del juego de azar'', al tomar una ruleta como un generador simple de números aleatorios. La llegada de las computadoras y el conocimiento del método por parte de universidades hicieron que el desarrollo de la metodología de Monte Carlo tuviera una velocidad vertiginosa y se convirtiera en una herramienta imprescindible para resolver problemas matemáticos a través de la generación de variables aleatorias.
Actualmente Monte Carlo es una metodología sumamente útil para resolver problemas no sólo de naturaleza estocástica sino también determinista, que no son solubles de forma analítica.
En el terreno actuarial y financiero, algunas de las posibles aplicaciones son:
- Determinación de pérdidas en un determinado riesgo
- Diseño de productos y estudio de su precio-tarificación
- Modelización de seguros de vida y rentas actuariales
- Análisis de inversión en activos
- Gestión de activos y pasivos
- Contrastación de la solvencia dinámica de una compañía
- Modelación del riesgo colectivo
SAS proporciona diversas técnicas de simulación de una variedad de modelos estadísticos, en donde las distribuciones puedes ser discretas, continuas, mixtas o multivariadas. En el siguiente vínculo web se pueden visualizar algunos ejemplos de aplicaciones SAS, con 10 técnicas que le permiten escribir simulaciones eficientes: https://support.sas.com/resources/papers/proceedings15/SAS1387-2015.pdf
Ahora bien, veámoslo aplicado a un caso sencillo de la vida real para entender cómo correr una simulación en SAS.
Sabemos que los bancos comúnmente usan modelos para hacer evaluaciones sobre los riesgos de una cartera de crédito en términos de distribuciones de probabilidad de pérdidas crediticias potenciales.
Los enfoques utilizados en la industria, para resolver el cálculo de evaluación de riesgo, incluyen modelos actuariales y matemáticos, así como modelos que utilizan simulaciones por computadora para generar la distribución de pérdidas.
Una forma flexible de obtener la distribuciones de pérdidas crediticias es a través de simulaciones de Monte Carlo utilizando el procedimiento de SAS denominado PROC IML (https://go.documentation.sas.com/?docsetId=imlug&docsetTarget=imlug_imlstart_sect012.htm&docsetVersion=15.1&locale=en).
Para tal ejemplo de simulación de Monte Carlo, se empleará un modelo de tipo unifactorial en su versión “default-mode”[1], es decir considerando la posibilidad binaria de default vs. cumplimiento normal, el cual es de amplio uso en la práctica bancaria de modelización del riesgo de crédito.
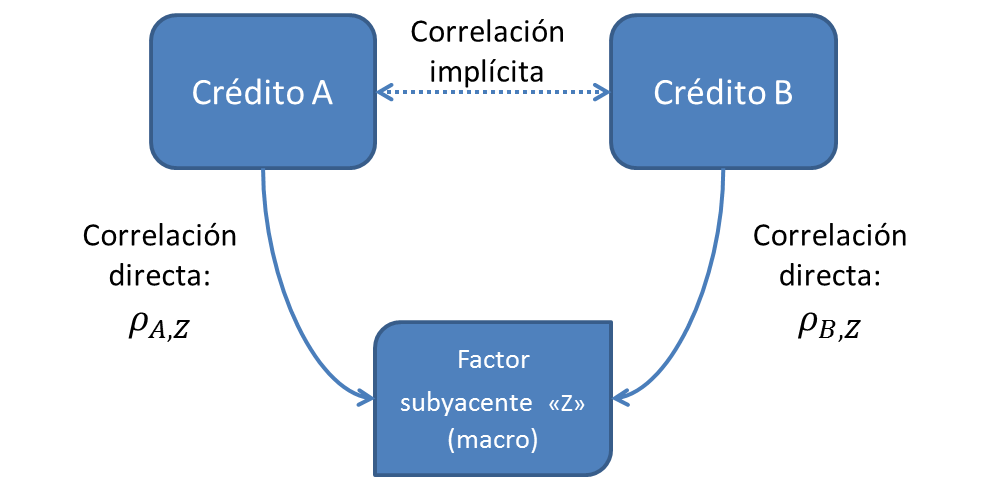
La ventaja de los modelos de tipo factoriales reside en que la correlación entre los créditos no necesita ser modelizada una a una, sino que cada crédito se correlacionará con un componente o “factor” exógeno (en este caso único). Así, la correlación entre cualquier par de créditos en la cartera se torna indirecta, a través de la correlación de cada uno de ellos con el factor en cuestión, como se puede apreciar en la figura que sigue:
El modelo además tiene fuerte razón económica ya que dicho factor bien podría representar el estado de la economía, el cual en mayor o menor medida afectará a todos los componentes de la cartera crediticia.
En línea con la propuesta de Merton (1974), el enfoque asume que el default de un crédito individual se producirá siempre que el valor de los activos financiados (A) caiga por debajo del valor de un punto crítico asociado a la deuda (C). Es decir:
Default ↔ A ≤ C (3)
No Default ↔ A > C
Específicamente, se asume que el rendimiento de los activos del deudor sigue una distribución log-normal, de modo que la trayectoria de los activos se puede asumir normal, según la siguiente especificación:
Contemplando lo mencionado, en el siguiente código SAS las variables aleatorias del modelo son establecidas por un generador de números aleatorios de acuerdo con una distribución especifica. En el precedente modelo establecido, los parámetros del modelo tienen que ser dados, y con una distribución normal estándar se simulan variables aleatorias a partir de las cuales va a dar lugar a la distribución de pérdidas. Luego se procede a que los datos se almacenen adecuadamente y puedan ser analizados por el PROC UNIVARIATE (utilizado principalmente para examinar la distribución de datos, incluida una evaluación de la normalidad y el descubrimiento de valores atípicos).
El siguiente es el procedimiento que ejemplifica cómo simular con SAS:
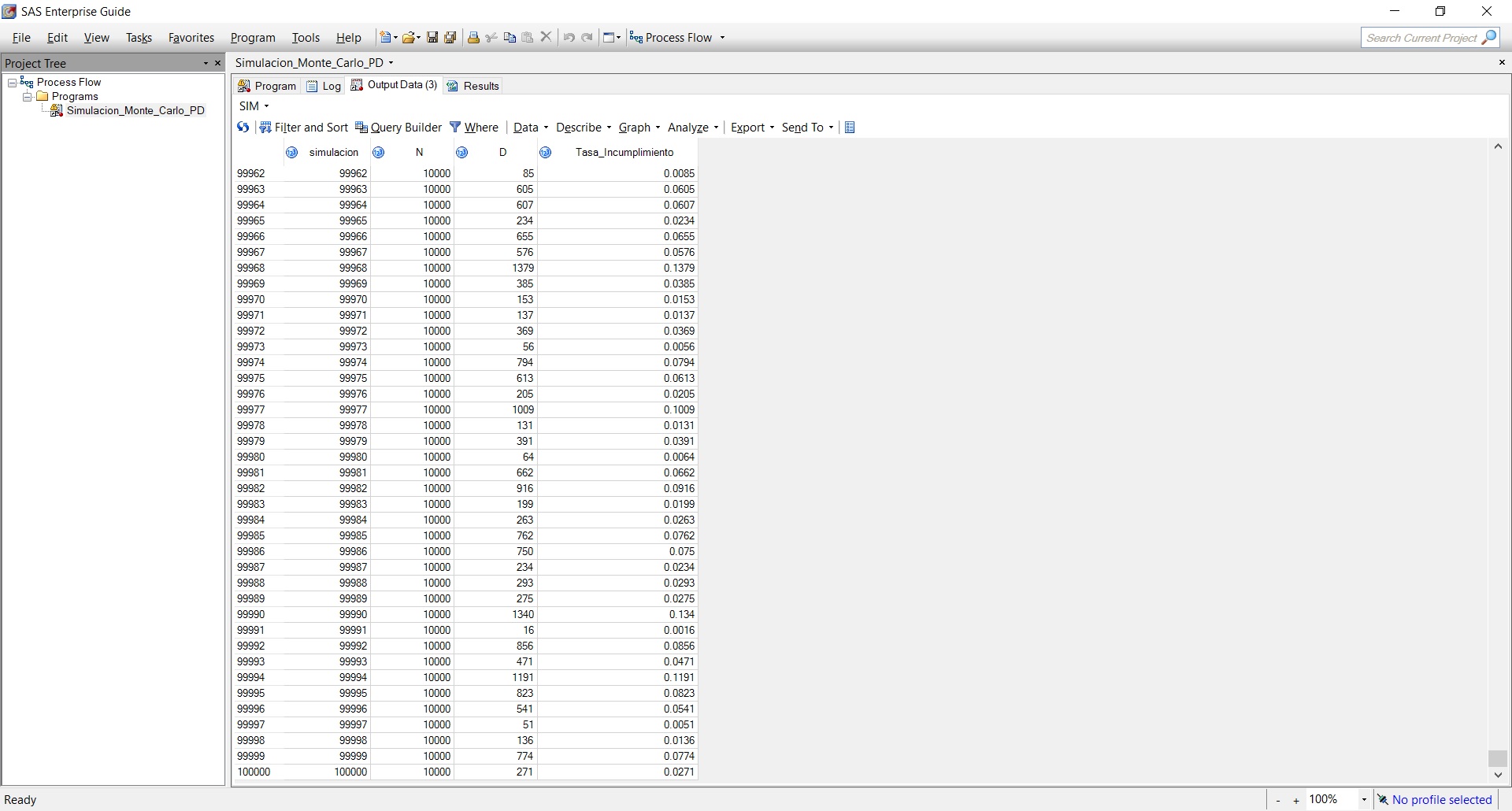
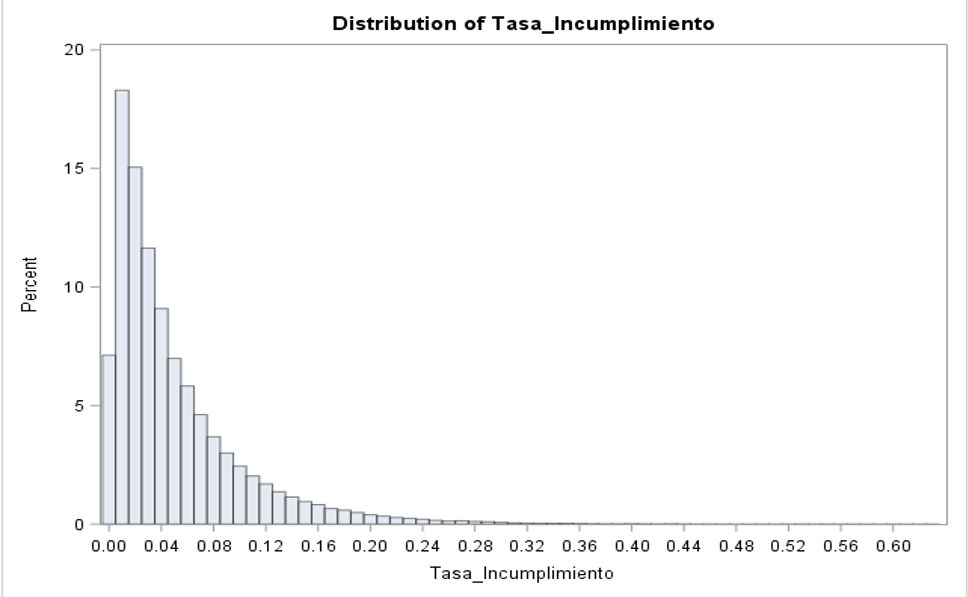
Una vez que corrió el proceso, obtenemos 100.000 simulaciones de la tasa de incumplimiento (default_rate). La tasa de incumplimiento puede interpretarse como una tasa de pérdida bajo el supuesto de una EAD (exposure at default) y una LGD (Loss given default) única.
Luego, generamos un histograma usando PROC UNIVARIATE para el número de observaciones en nuestro conjunto de datos de salida:
Y obtenemos lo siguientes estadísticos:
Y el siguiente gráfico de distribución:
Análisis Bayesiano:
Entendido el Concepto de Simulación de Monte Carlo, hablemos ahora del análisis bayesiano.
Les cuento que el primer gran tratado sobre probabilidad que combina la teoría acerca de esa materia con el cálculo es la “Teoría analítica de las probabilidades”, del matemático y astrónomo francés Pierre Simon Laplace. La teoría de la probabilidad se centra en los fenómenos aleatorios. El simple fenómeno de un dado puede considerarse un suceso aleatorio, pero después de muchas repeticiones se hace patente la existencia de una padrón estadístico que puede utilizarse para hacer predicciones.
Dentro de las aplicaciones de la teoría de la probabilidad es válido enunciar el uso de métodos bayesianos, que se ha vuelto cada vez más popular en el análisis estadístico moderno, con aplicaciones en una amplia variedad de campos científicos.
En términos de probabilidad, el Teorema de Bayes hace referencia a aquella información que es empleada para saber cuál es la probabilidad condicional que tiene un suceso. Este teorema fue desarrollado por el matemático Thomas Bayes. Su intención era determinar la probabilidad de un suceso con respecto a la probabilidad de otro suceso diferente.
Una vez que ya sabemos la definición del Teorema de Bayes debemos tener en cuenta qué pasos debemos seguir para calcular y determinar la probabilidad que nos interesa. La fórmula de dicho teorema es la siguiente:
En esta fórmula, A y B forman parte de los sucesos probables que se deben interpretar. Para calcular el Teorema de Bayes, deberemos tener en cuenta los siguientes datos. Por un lado, P(A) será la probabilidad a priori. Por otro lado, P(B|A) será la probabilidad que tenga B con respecto a la hipótesis dada de A, que son las verosimilitudes. Por último, P(A|B) serán las probabilidades a posteriori.
Cabe destacar que todo el mundo emplea “conceptos bayesianos” para navegar por su vida cotidiana, tal vez sin ser consciente de que lo está haciendo. Usted confía en experiencias pasadas para evaluar el riesgo, asignar causa probable, navegar por la incertidumbre y predecir el futuro. Esta forma de procesar información y tomar decisiones es lo que refleja el razonamiento bayesiano, una construcción matemática que permite la posibilidad de incorporar conocimiento previo o información existente (basada en opinión experta, estudios pasados, etc.) al análisis de datos actual. Esta información existente está representada por una distribución previa, y la probabilidad de los datos se pondera efectivamente por la distribución previa, a medida que se calculan los resultados del análisis de datos. En otras palabras, la inferencia bayesiana combina la experiencia pasada con la información actual para asignar motivo probable, permitiendo contemplar la probabilidad como una forma de conocimiento en función de la experiencia que se va adquiriendo.
Hay varias ventajas asociadas con este enfoque para inferencia estadística. Algunas de las ventajas de adoptar métodos bayesianos incluyen su capacidad de utilizar información previa e interpretar las inferencias de una manera más estrechamente alineada con la toma de decisiones naturales.
Ahora bien, en esencia la estadística bayesiana trata los parámetros como variables aleatorias desconocidas, y hace inferencias basadas en las distribuciones posteriores de los parámetros. En todos los casos, excepto en los más simples, es muy difícil obtener la distribución posterior de manera directa y analítica. A menudo, los métodos bayesianos se basan en simulaciones para generar muestras a partir de la distribución posterior deseada y usan los valores simulados para aproximar la distribución y hacer las inferencias.
SAS cuenta con un procedimiento denominado PROC MCMC, que es un procedimiento flexible basado en simulación que es adecuado para adaptarse a una amplia gama de modelos bayesianos.
Para usar PROC MCMC, se debe especificar una función de probabilidad para los datos y una distribución previa para los parámetros. Es posible encontrar información acerca de este procedimiento en https://support.sas.com/documentation/onlinedoc/stat/142/mcmc.pdf.
Veámoslo con un ejemplo. Supongamos los siguientes datos hipotéticos de reclamos de seguro de automóviles.
La variable “n” representa el número de titulares de pólizas de seguro y la variable “c” representa el número de reclamos de seguro. La variable “automóvil” es el tipo de automóvil involucrado (clasificado en tres grupos). La variable “edad” es el grupo de edad del titular de la póliza (clasificado en dos grupos).
Adicionalmente, supongamos que el número de reclamos de seguros (variable “c”) tiene una distribución de probabilidad de Poisson y que su media está relacionada con los factores “edad” y “automóvil”.
Luego, procedemos a correr el procedimiento PROC MCMC. Hay cuatro parámetros en el modelo: alpha es la intersección; beta_automovil1 y beta_automovil2 son coeficientes para la variable automóvil, que tiene tres niveles; y beta_edad es el coeficiente para la variable edad. La instrucción PRIOR determina la distribución previa de los parámetros del modelo, en donde se especificó que el valor predeterminado de los coeficientes sigue una distribución normal con media 0, mientras que la declaración MODEL establece la distribución condicional de los datos dados los parámetros.
Corriendo el “PROC MCMC” obtenemos un resumen para la simulación de la distribución posterior de los parámetros, como se puede apreciar en la siguiente imagen:
Ahora bien, también se puede ajustar el mismo modelo usando el procedimiento GENMOD, el cual hemos mencionado en la entrega número 5 del Sommelier del riesgo, agregando la instrucción Bayes.
Obteniendo:
Las estimaciones posteriores son similares, pero no exactamente iguales, al PROC MCMC. Esto es debido a la naturaleza de la simulación y los diferentes algoritmos que utilizan los procedimientos comparados.
Hemos finalizado en el día de hoy una mínima explicación de estas dos técnicas. ¡Los espero en la próxima entrega!




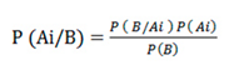







2 Comments
Gracias por las explicaciones y los ejemplos. En particular, me gusta mucho el PROC IML para las simulaciones pues con pocas líneas de código se pueden obtener resultados rápidamente, además de que las matrices son muy prácticas para este tipo de problemas.
Gracias por tus comentarios!