Advanced Analytics Archives

Advanced Analytics

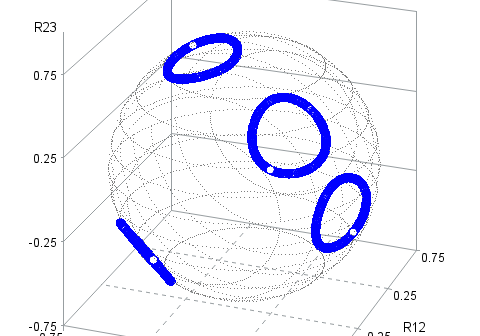
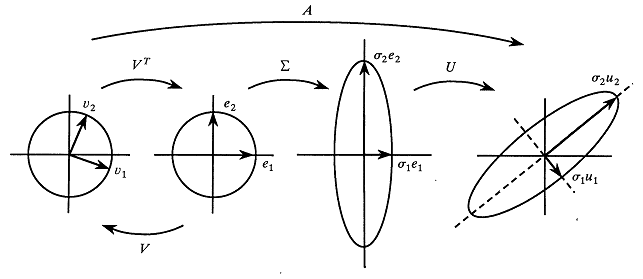
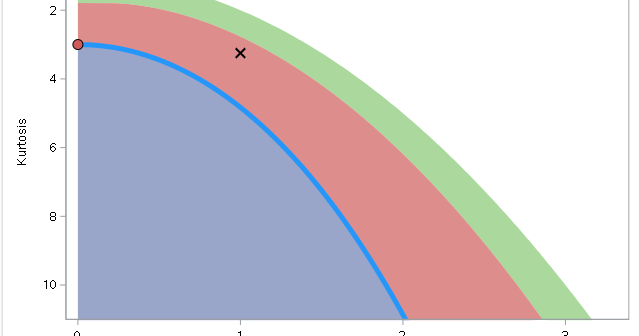
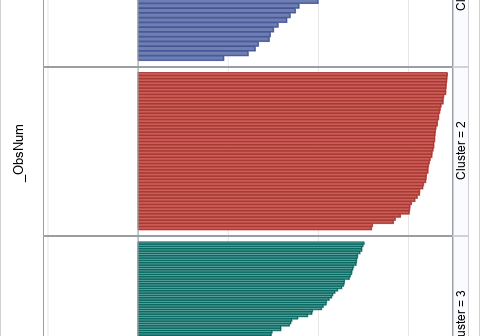
Move beyond spreadsheets to data mining, forecasting, optimization – and more

Advanced Analytics | Learn SAS | Machine Learning

Rick WicklinJune 30, 2025 0

An application of Latin hypercube sampling to optimization

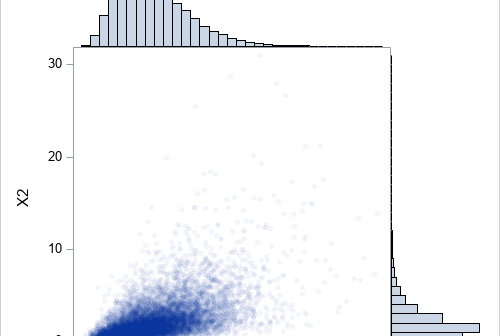
A previous article discusses a "Catch-22" paradox for fitting nonlinear regression models: You can't estimate the parameters until you fit the model, but you can't fit the model until you provide an initial guess for the parameters! If your initial guess for the parameters is not good enough, the nonlinear

English

Advanced Analytics | Data Visualization | Learn SAS

Rick WicklinJune 23, 2025 0

How to add a curve to a moment-ratio diagram

I have previously written about the moment-ratio diagram as a graphical tool for modeling univariate distributions and also as a tool for examining the distribution of the skewness and kurtosis statistics for distributions. The simple moment-ratio (M-R) diagram from my book (Wicklin, 2013, Simulating Data with SAS, Chapter 16) is

English

Advanced Analytics | Machine Learning

Rick WicklinMay 5, 2025 0

Implement a SMOTE simulation algorithm in SAS

A recent article describes the main features of simulation by using the Synthetic Minority Over-sampling Technique (SMOTE). SMOTE was created to oversample from a set of rare events prior to running a machine learning classification algorithm. However, at its heart, the SMOTE algorithm (Chawla et al., 2002) provides a way

English

Advanced Analytics | Data Visualization

Rick WicklinJanuary 15, 2025 0

Visualize correlation matrices that have the same eigenvalues

A colleague asked me an interesting question: Suppose you have a structured correlation matrix, such as a matrix that has a compound symmetric, banded, or an AR1(ρ) structure. If you generate a random correlation matrix that has the same eigenvalues as the structured matrix, does the random matrix have the

English

Advanced Analytics

Geometric interpretation of the singular value decomposition (SVD) as the product of a rotation/reflection, followed by a scaling, followed by another rotation/reflection.

Rick WicklinJanuary 8, 2025 3

Matrix norms and spectra

A previous article discusses covariance matrices that have the same set of eigenvalues. The set of eigenvalues is called the spectrum of the matrix. For symmetric matrices, the spectrum contains real numbers. For covariance matrices, which are positive semidefinite, the eigenvalues are nonnegative. It turns out that two symmetric matrices

English

Advanced Analytics | Programming Tips

Rick WicklinDecember 9, 2024 0

Latin hypercube sampling in SAS

While researching the topic of Latin hypercube sampling (LHS), I read an article by Emily Gao (2019) that shows how to use PROC IML in SAS to perform the algorithm. It is possible to simplify Gao's implementation of Latin hypercube sampling in SAS while also making the computation more efficient.

English

Advanced Analytics | Learn SAS

Rick WicklinNovember 11, 2024 0

Introducing PROC SIMSYSTEM in SAS Viya

When the SAS Global Forum 2020 conference was cancelled by the global COVID-19 pandemic, I felt sorry for the customers and colleagues who had spent months preparing their presentations. One presentation I especially wanted to attend was by Bucky Ransdell and Randy Tobias: "Introducing PROC SIMSYSTEM for Systematic Nonnormal Simulation".

English

Advanced Analytics | Data Visualization | Programming Tips

Rick WicklinMay 17, 2023 1

Compute the silhouette statistic in SAS

A previous article defines the silhouette statistic (Rousseeuw, 1987) and shows how to use it to identify observations in a cluster analysis that are potentially misclassified. The article provides many graphs, including the silhouette plot, which is a bar chart or histogram that displays the distribution of the silhouette statistic

English

Advanced Analytics

Rick WicklinJuly 5, 2021 18

An introduction to simulating correlated data by using copulas

Do you know what a copula is? It is a popular way to simulate multivariate correlated data. The literature for copulas is mathematically formidable, but this article provides an intuitive introduction to copulas by describing the geometry of the transformations that are involved in the simulation process. Although there are

Advanced Analytics | Learn SAS

Rick WicklinSeptember 14, 2020 0

Video: How to Write a Custom Parallel Program in SAS Viya

My 2020 SAS Global Forum paper was about how to write custom parallel programs by using the iml action in SAS Viya 3.5. My conference presentation was canceled because of the coronavirus pandemic, but I recently recorded a 15-minute video that summarizes the main ideas in the paper. One of

English

Blogs

Blogs

Advanced Analytics