A previous article discusses covariance matrices that have the same set of eigenvalues. The set of eigenvalues is called the spectrum of the matrix. For symmetric matrices, the spectrum contains real numbers. For covariance matrices, which are positive semidefinite, the eigenvalues are nonnegative.

It turns out that two symmetric matrices that have the same spectrum also have the same matrix norm. This is obvious for the L2 matrix norm, but less obvious for the Frobenius norm. This article shows that if A and B are two symmetric matrices that have the same spectrum, then || A || = || B ||, where the norm is either the L2 norm or the Frobenius norm.

Two matrix norms

Two popular matrix norms are the L2 norm and the Frobenius norm:

• The L2 norm (also called the spectral norm) is the magnitude of the largest eigenvalue. For positive definite matrices, the L2 norm is the largest eigenvalue.
• The Frobenius norm is the square root of the sum of the squared elements in the matrix. Equivalently, the squared Frobenius norm is the sum of squares of the matrix elements. That is, for the matrix A,
  $\|A\|_{\text{F}}^2 = \sum _i \sum _j A_{ij}^2.$
  As shown in Wikipedia, this quantity is also equal to the trace of the crossproducts matrix, A`*A:
  $\|A\|_{\text{F}}^2 = \text{trace} \left(A^{\prime}A\right)$

The Frobenius norm does not seem to be related to eigenvalues, but in fact it is! As shown below, the squared Frobenius norm equals the sum of the squared elements of the spectrum.

The spectrum determines the L2 norm

By definition, any two matrices that have the same spectrum must have the same L2 norm. Because they have the same spectrum, the largest eigenvalue is the same.

The spectrum determines the Frobenius norm for symmetric matrices

Given a spectrum, every symmetric matrix with that spectrum has the same Frobenius norm. By the spectral decomposition theorem, every symmetric matrix can be decomposed as A = Q*diag(L)*Q`, where L is the spectrum vector and Q is an orthogonal matrix. As shown in the Appendix, the orthogonal matrices do not change the Frobenius norm. Therefore, $\|A\|_F = \|\text{diag}(L)\|_F$.

Not only does every symmetric matrix with a given spectrum has the same Frobenius norm, but we know exactly what the value of the norm is! The squared Frobenius norm equals the sum of the squared elements of the spectrum: $\|A\|_F^2 = \sum_i \lambda_i^2$, where $L=\{\lambda_1, \lambda_2, ..., \lambda_n\}$ is the spectrum of A. Equivalently, the Frobenius norm equals the Euclidean length of the vector L.

Example: Two covariance matrices that have the same eigenvalues

A previous article shows how to generate random covariance matrices that have the same set of eigenvalues. The following 4 x 4 symmetric matrices are from that article. You can use the SAS IML language to show that they have the same set of eigenvalues:

proc iml;
S1 = {
1.6777914558 -0.387406153 -0.443734244 0.0068766222 ,
-0.387406153 0.9137286028 -0.01915772 -0.058629084  ,
-0.443734244 -0.01915772 0.842547134 -0.348769043   ,
0.0068766222 -0.058629084 -0.348769043 0.5659328073 };
 
S2 = {
0.7912845768 0.0216179596 -0.193768339 -0.350178629 ,
0.0216179596 0.7775696813 -0.039066959 -0.295580783 ,
-0.193768339 -0.039066959 1.7418846881 0.4392865998 ,
-0.350178629 -0.295580783 0.4392865998 0.6892610538 };
 
eval1 = eigval(S1);
eval2 = eigval(S2);
print eval1 eval2;

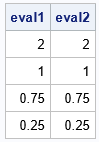
Today's article proves that these matrices also have the same L2 norm and Frobenius norms. The following statements use the NORM function in SAS IML to compute the norms for each matrix:

L2Norm1 = norm(S1, "L2");
L2Norm2 = norm(S2, "L2");
print L2Norm1 L2Norm2;
 
FrobNorm1 = norm(S1, "Frob");
FrobNorm2 = norm(S2, "Frob");
print FrobNorm1 FrobNorm2;

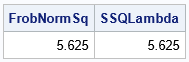
In addition, the squared Frobenius norm equals the sum of the squares of the spectrum:

FrobNormSq = FrobNorm1**2;
SSQLambda = SSQ(eval1);
print FrobNormSq SSQLambda;

What about other matrix norms?

Other matrix norms, such as the L₁ and L_∞ norms, do not have this property. That is, if A and B have the same spectrum, they do not necessarily have the same L₁ and L_∞ norms. For example, the 4 x 4 symmetric matrices in the previous section do not have the same L₁ or L_∞ norms.

Summary

The squared Frobenius norm is the sum of the squares of the elements in a matrix. This quantity seems to be unrelated to eigenvalues. Nevertheless, this article shows that for symmetric matrices, the squared Frobenius norm equals the sum of the squares of the eigenvalues.

Appendix: The Frobenius norm is unchanged by orthogonal transformations

Theorem 1: If A and Q are square matrices and Q is orthogonal, then $\|QA\|_F = \|A Q\|_F = \|A\|_F$ for the Frobenius norm.

If Q is an orthogonal matrix, then Q`*Q = I. To prove the theorem, the following lemmas are helpful:

• Lemma 1: The trace of a product. If A is an m x n matrix and B is an n x m matrix, then tr(AB) = tr(BA).
• Lemma 2: The cyclic property. If A, B, and C are square matrices, then tr(ABC) = tr(BCA) = tr(CAB). That is, the trace is invariant if you move the first matrix to the end of the multiplication chain. The proof follows from Lemma 1. Although stated for three matrices, it obviously extends to a chain of arbitrarily many matrices.
• Lemma 3: If Q is an orthogonal matrix, then $\text{tr}(QAQ^{\prime}) = \text{tr}(A)$. This is an application of Lemma 2 (the cyclic property) and the fact that Q`*Q=I for an orthogonal matrix.

To prove Theorem 1, use the trace definition of the Frobenius norm.

First, consider B = Q*A. Then
$\|B\|_F^2 = \text{tr}(B^{\prime}B) = \text{tr}((QA)^{\prime}(QA)) = \text{tr}(A^{\prime} Q^{\prime} Q A) = \text{tr}(A^{\prime} A) = \|A\|_F^2$.
This proves the first half of the theorem.

Next, consider B = A*Q. Then
$\|B\|_F^2 = \text{tr}(B^{\prime}B) = \text{tr}((AQ)^{\prime}(AQ)) = \text{tr}(Q^{\prime} A^{\prime} A Q)$.
Apply Lemma 3 to the crossproducts matrix, A`*A:
$\text{tr}(Q^{\prime} A^{\prime} A Q) = \text{tr}(A^{\prime}A) = \|A\|_F^2$.

This theorem shows that orthogonal transformations such as rotations, reflections, and their compositions do not affect the Frobenius norm of a matrix.