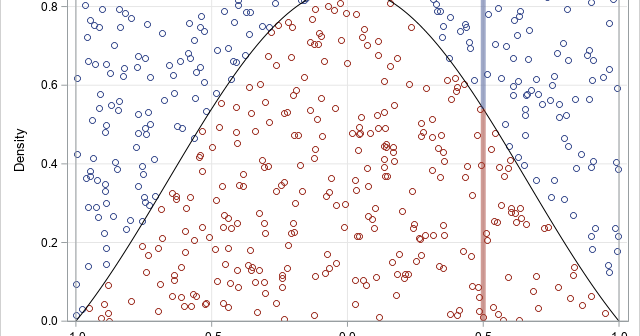
The acceptance-rejection method (sometimes called rejection sampling) is a method that enables you to generate a random sample from an arbitrary distribution by using only the probability density function (PDF). This is in contrast to the inverse CDF method, which uses the cumulative distribution function (CDF) to generate a random