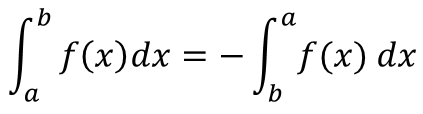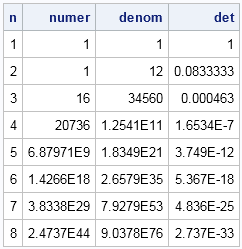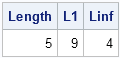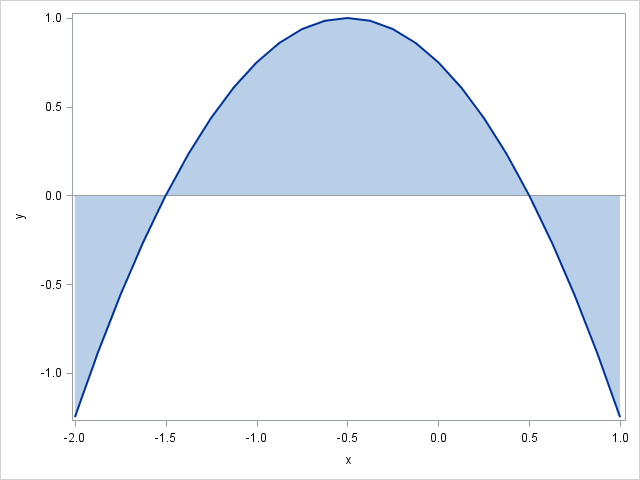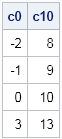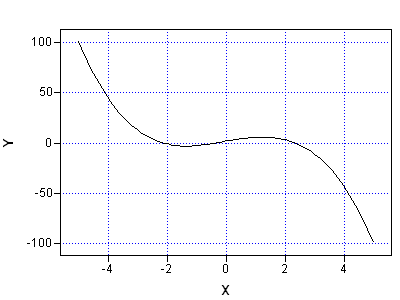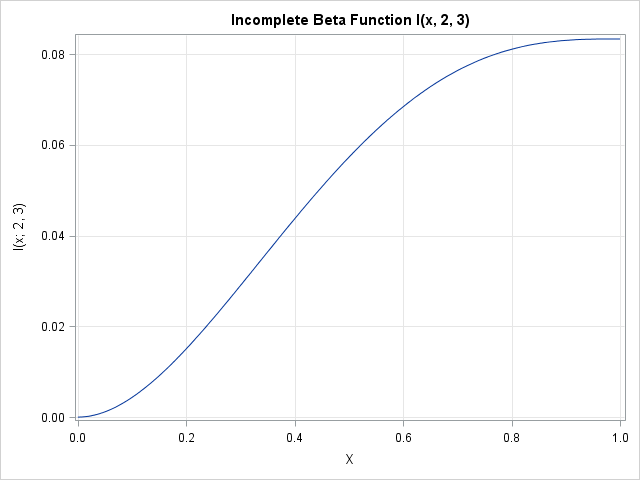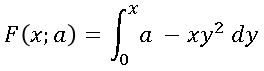
The SAS/IML language is used for many kinds of computations, but three important numerical tasks are integration, optimization, and root finding. Recently a SAS customer asked for help with a problem that involved all three tasks. The customer had an objective function that was defined in terms of an integral.