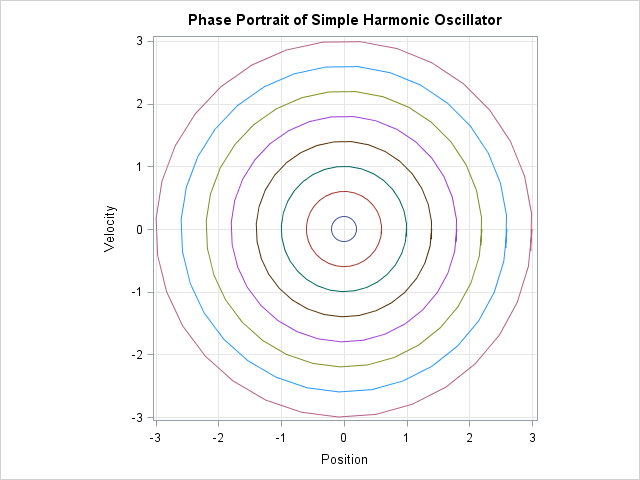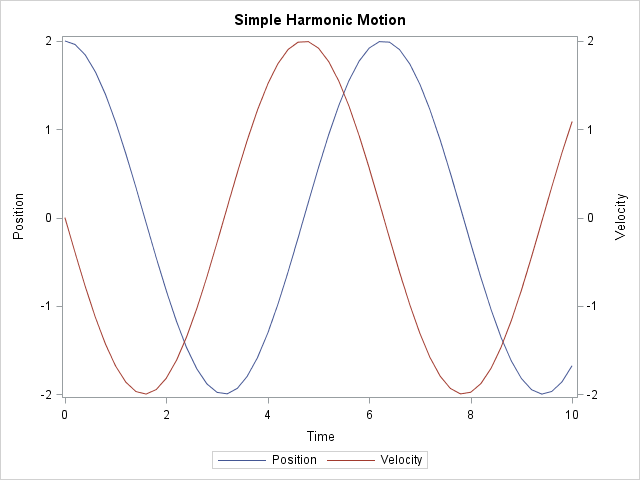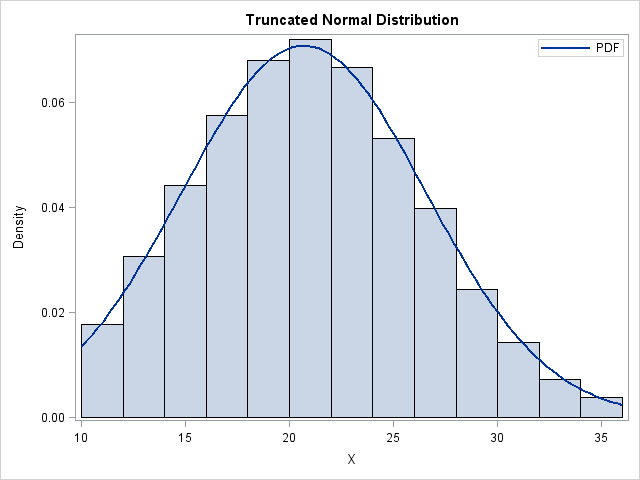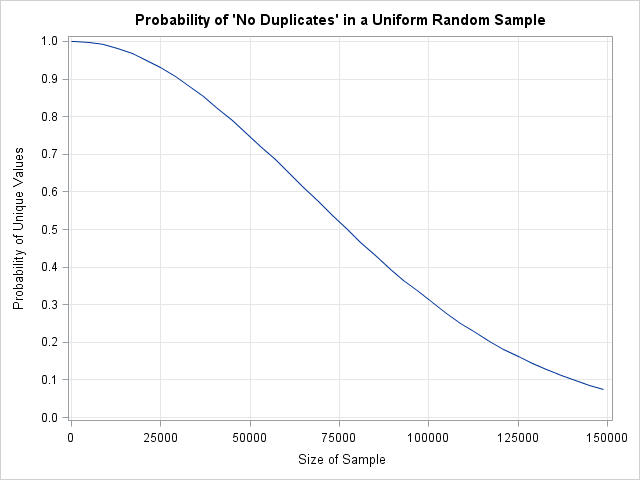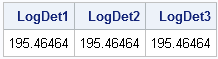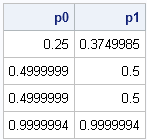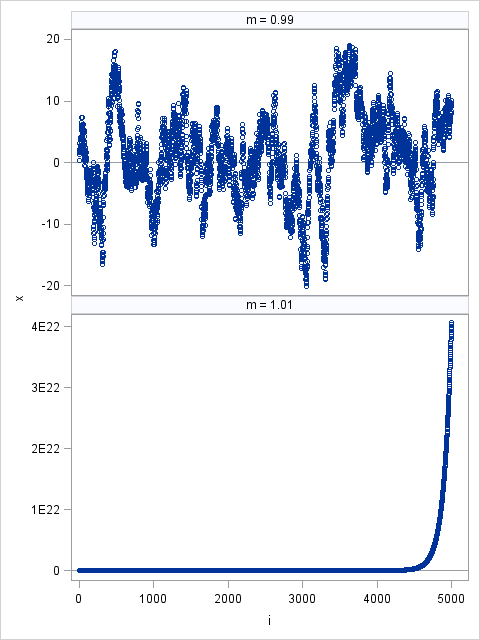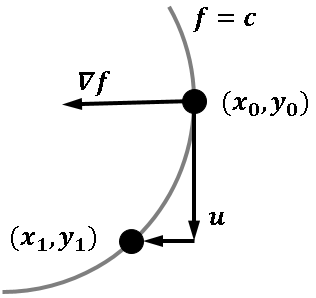
Like many other computer packages, SAS can produce a contour plot that shows the level sets of a function of two variables. For example, I've previously written blogs that use contour plots to visualize the bivariate normal density function and to visualize the cumulative normal distribution function. However, sometimes you