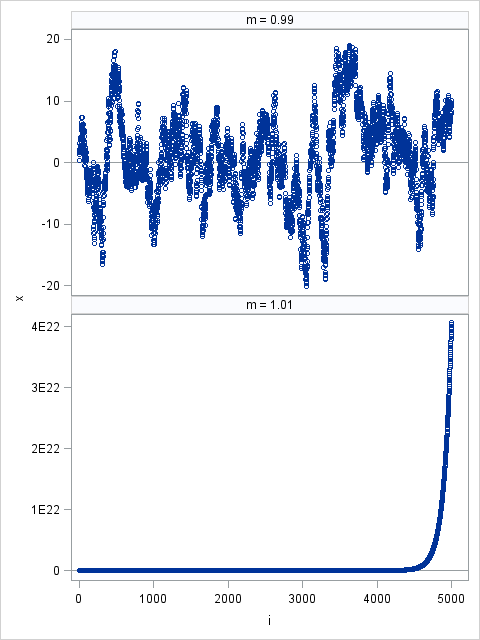
A collegue who works with time series sent me the following code snippet. He said that the calculation was overflowing and wanted to know if this was a bug in SAS: data A(drop=m); call streaminit(12345); m = 2; x = 0; do i = 1 to 5000; x = m*x
I've been a fan of statistical simulation and other kinds of computer experimentation for many years. For me, simulation is a good way to understand how the world of statistics works, and to formulate and test conjectures. Last week, while investigating the efficiency of the power method for finding dominant
When I was at SAS Global Forum last week, a SAS user asked my advice regarding a SAS/IML program that he wrote. One step of the program was taking too long to run and he wondered if I could suggest a way to speed it up. The long-running step was
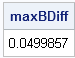
To a statistician, the DIF function (which was introduced in SAS/IML 9.22) is useful for time series analysis. To a numerical analyst and a statistical programmer, the function has many other uses, including computing finite differences. The DIF function computes the difference between the original vector and a shifted version
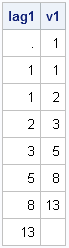
To a statistician, the LAG function (which was introduced in SAS/IML 9.22) is useful for time series analysis. To a numerical analyst and a statistical programmer, the function provides a convenient way to compute quantitites that involve adjacent values in any vector. The LAG function is essentially a "shift operator."
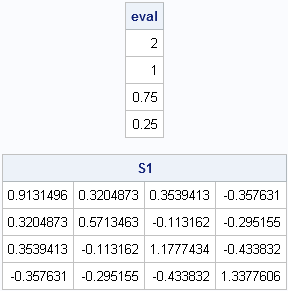
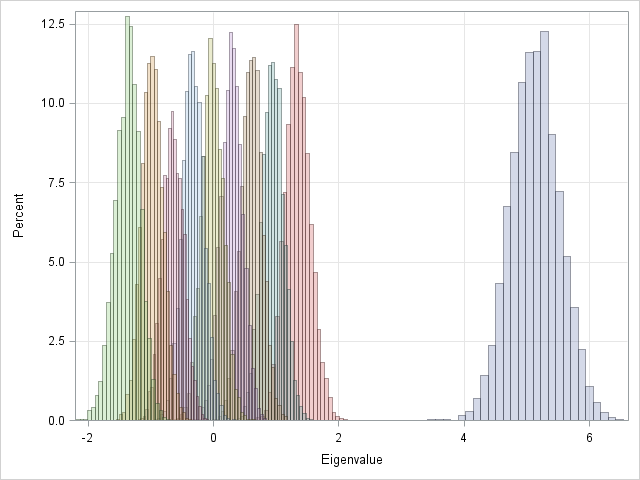
In a previous post I showed how to implement Stewart's (1980) algorithm for generating random orthogonal matrices in SAS/IML software. By using the algorithm, it is easy to generate a random matrix that contains a specified set of eigenvalues. If D = diag(λ1, ..., λp) is a diagonal matrix and
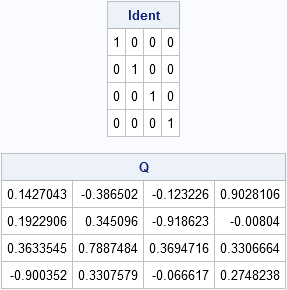
Because I am writing a new book about simulating data in SAS, I have been doing a lot of reading and research about how to simulate various quantities. Random integers? Check! Random univariate samples? Check! Random multivariate samples? Check! Recently I've been researching how to generate random matrices. I've blogged
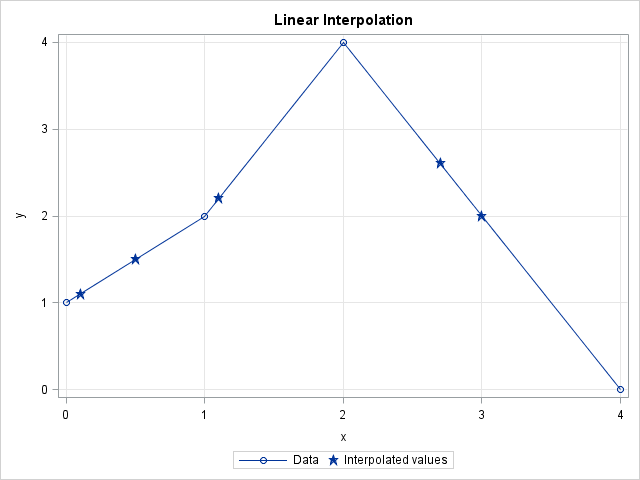
A recent discussion on the SAS-L discussion forum concerned how to implement linear interpolation in SAS. Some people suggested using PROC EXPAND in SAS/ETS software, whereas others proposed a DATA step solution. For me, the SAS/IML language provides a natural programming environment to implement an interpolation scheme. It also provides
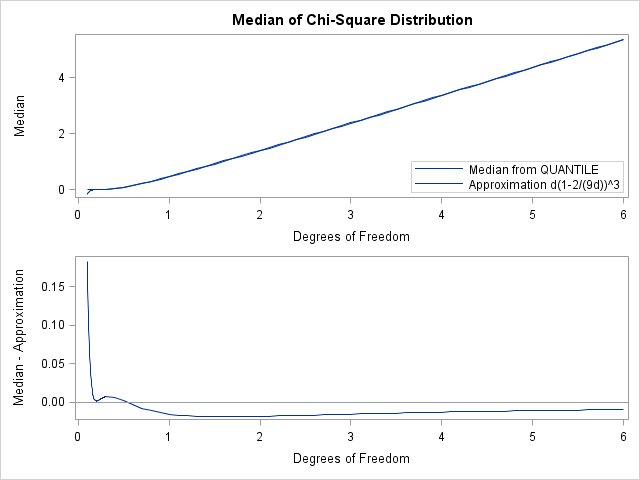
I was at the Wikipedia site the other day, looking up properties of the Chi-square distribution. I noticed that the formula for the median of the chi-square distribution with d degrees of freedom is given as ≈ d(1-2/(9d))3. However, there is no mention of how well this formula approximates the
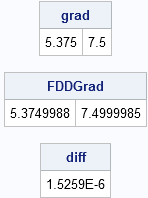
I previously wrote about using SAS/IML for nonlinear optimization, and demonstrated optimization by maximizing a likelihood function. Many well-known optimization algorithms require derivative information during the optimization, including the conjugate gradient method (implemented in the NLPCG subroutine) and the Newton-Raphson method (implemented in the NLPNRA method). You should specify analytic
