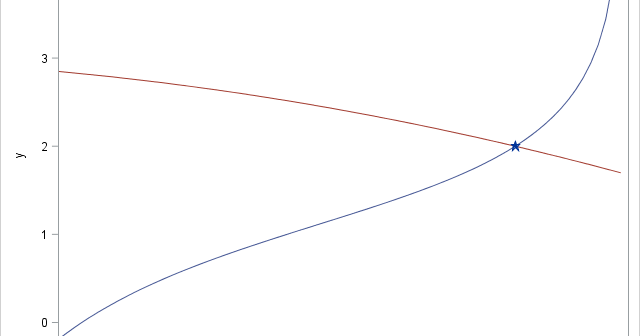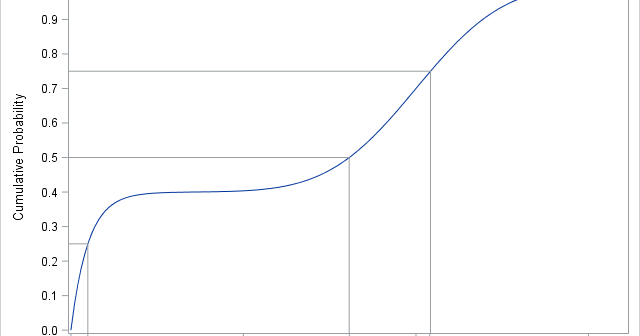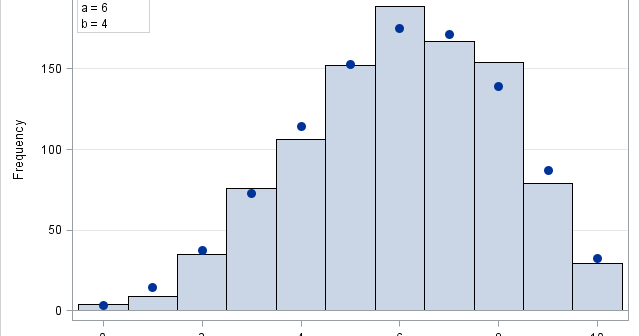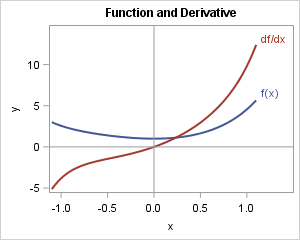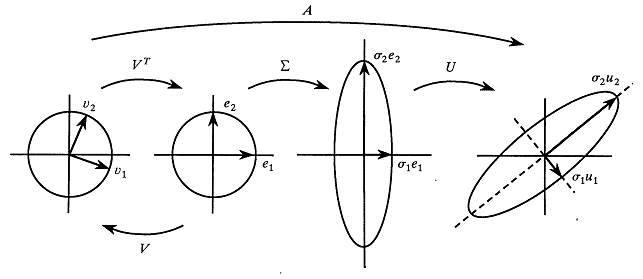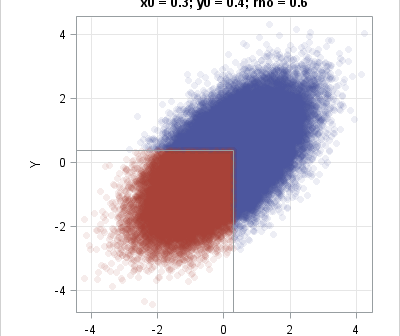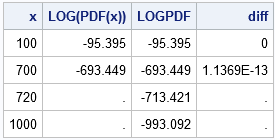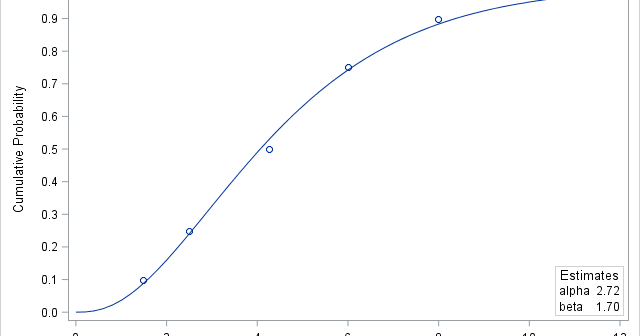
Data analysts often fit a probability distribution to data. When you have access to the data, a common technique is to use maximum likelihood estimation (MLE) to compute the parameters of a distribution that are "most likely" to have produced the observed data. However, how can you fit a distribution