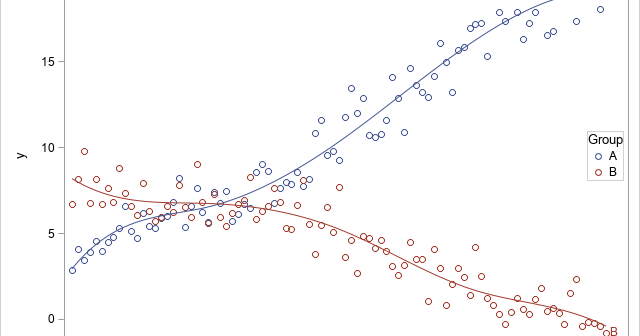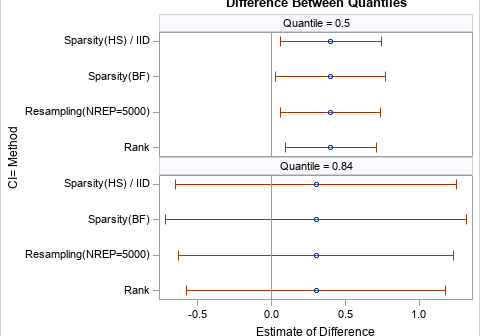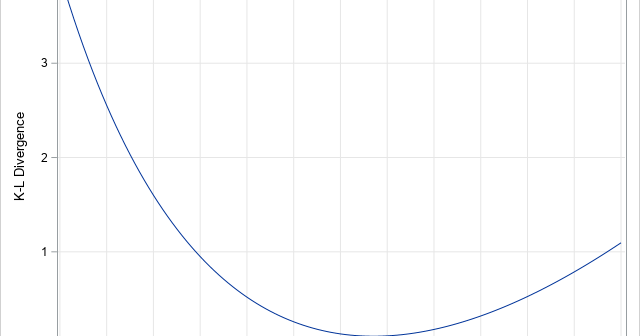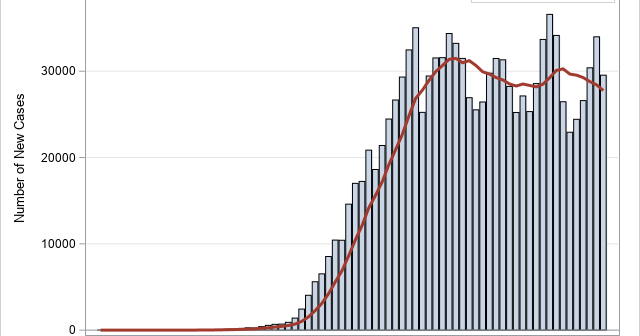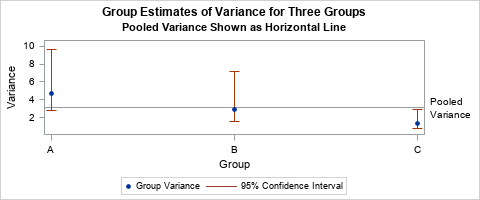
The first time I saw a formula for the pooled variance, I was quite confused. It looked like Frankenstein's monster, assembled from bits and pieces of other quantities and brought to life by a madman. However, the pooled variance does not have to be a confusing monstrosity. The verb "to