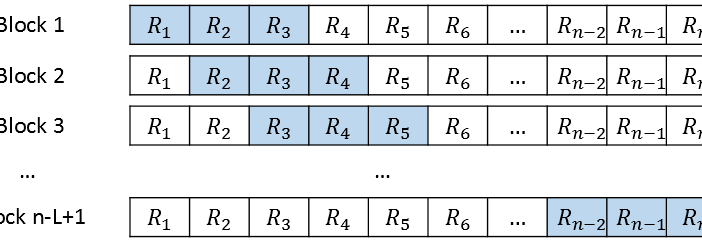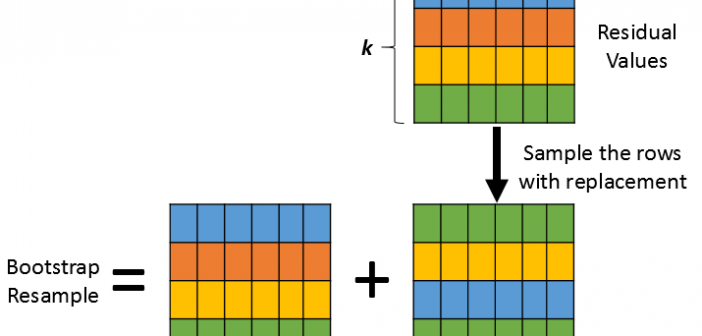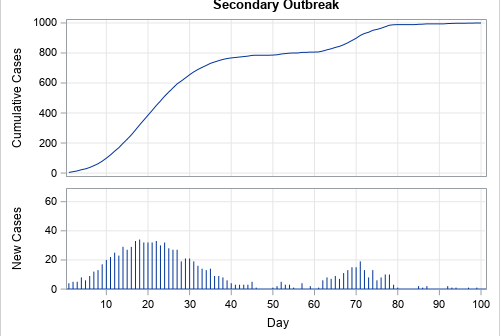
This is the third and last introductory article about how to bootstrap time series in SAS. In the first article, I presented the simple block bootstrap and discussed why bootstrapping a time series is more complicated than for regression models that assume independent errors. Briefly, when you perform residual resampling