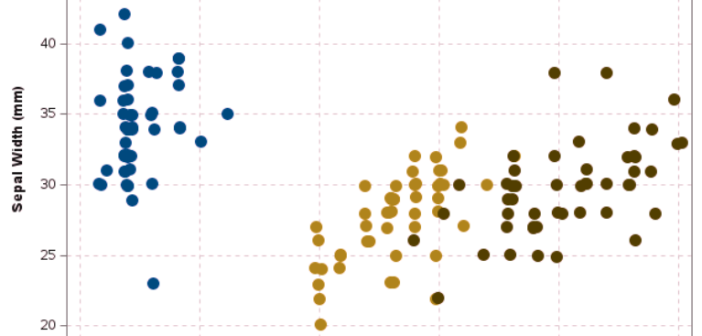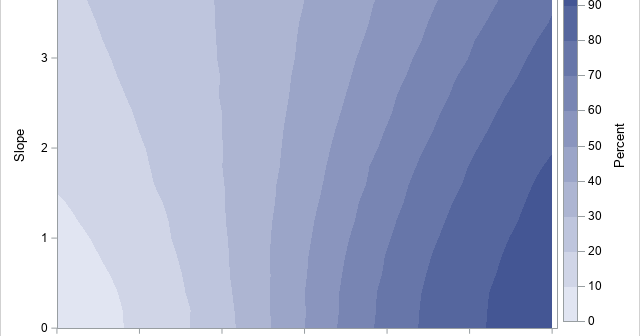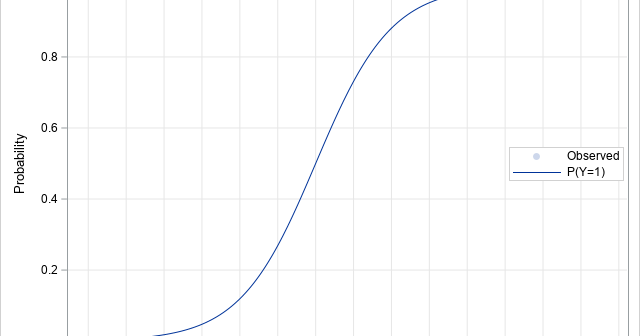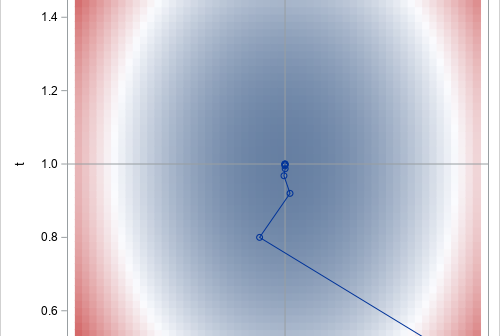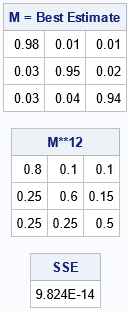
You can use a Markov transition matrix to model the transition of an entity between a set of discrete states. A transition matrix is also called a stochastic matrix. A previous article describes how to use transition matrices for stochastic modeling. You can estimate a Markov transition matrix by using