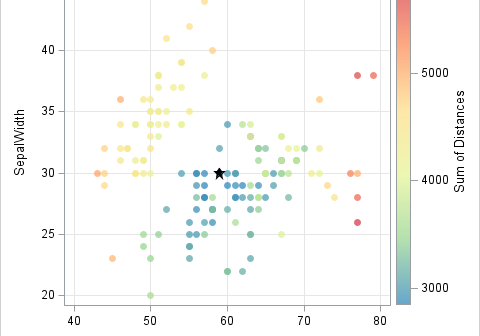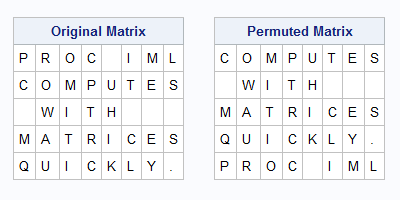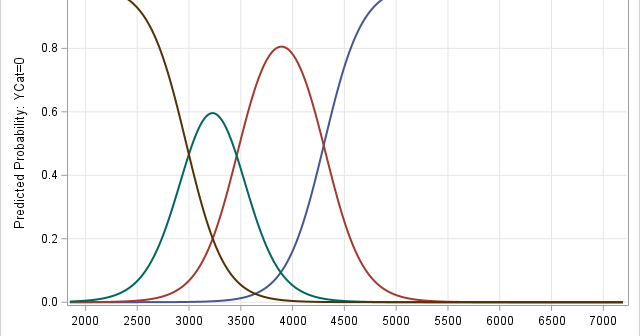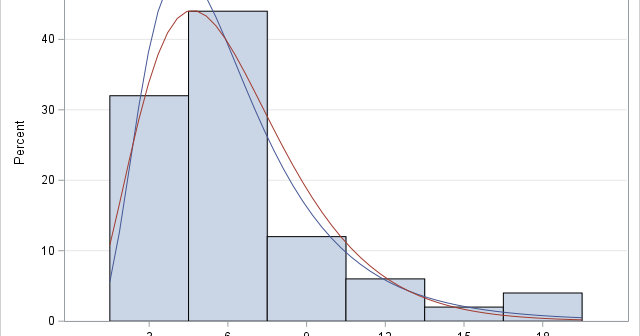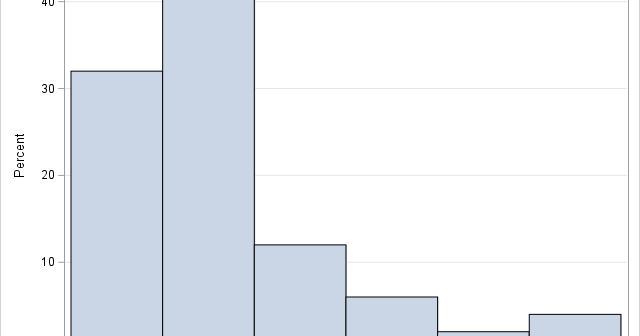
Rockin' around the Christmas tree, Have a happy holiday – Brenda Lee An internet search for "How many lights do I need for my Christmas tree," returns many opinions. A popular answer is that you need "one strand of lights for each foot of your tree." Another common answer is