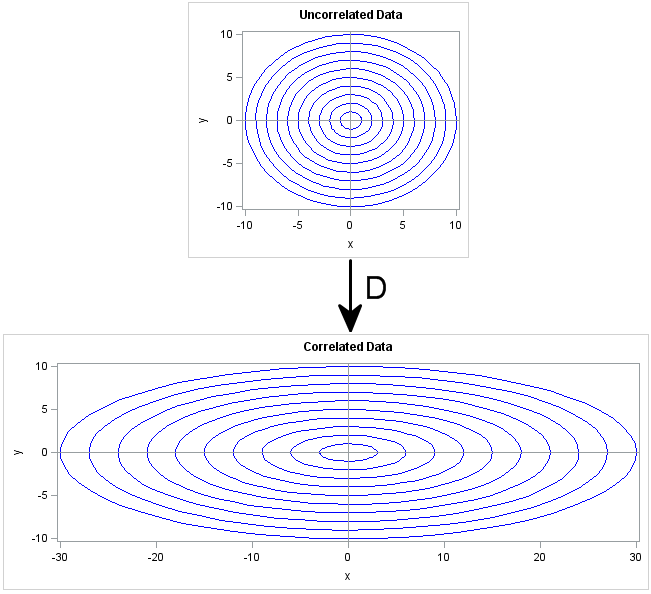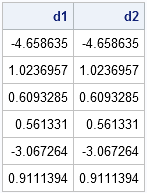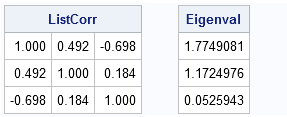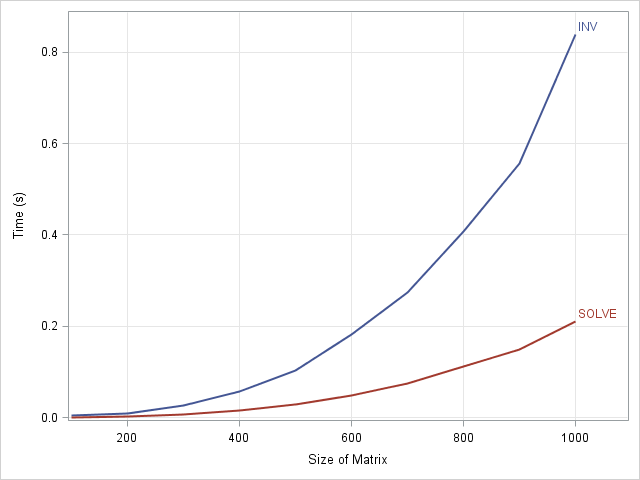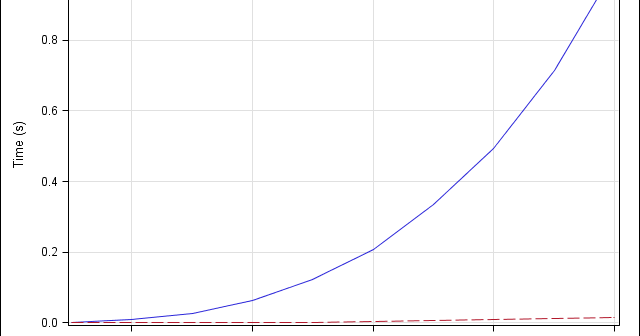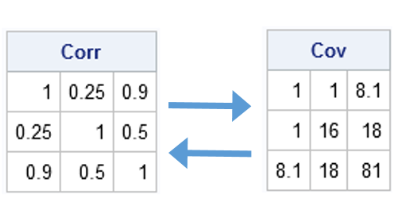
I have previously blogged about how to convert a covariance matrix into a correlation matrix in SAS (and the other way around). However, I still get questions about it, perhaps because my previous post demonstrated more than one way to accomplish each transformation. To eliminate all confusion, the following SAS/IML
A variance-covariance matrix expresses linear relationships between variables. Given the covariances between variables, did you know that you can write down an invertible linear transformation that "uncorrelates" the variables? Conversely, you can transform a set of uncorrelated variables into variables with given covariances. The transformation that works this magic is
Once again I rediscovered something that I once knew, but had forgotten. Fortunately, this blog is a good place to share little code snippets that I don't want to forget. I needed to compute the diagonal elements of a product of two matrices. In symbols, I have an nxp matrix,
It is "well known" that the pairwise deletion of missing values and the resulting computation of correlations can lead to problems in statistical computing. I have previously written about this phenomenon in my article "When is a correlation matrix not a correlation matrix." Specifically, consider the symmetric array whose elements
Birds migrate south in the fall. Squirrels gather nuts. Humans also have behavioral rituals in the autumn. I change the batteries in my smoke detectors, I switch my clocks back to daylight standard time, and I turn the mattress on my bed. The first two are relatively easy. There's even
I've previously described ways to solve systems of linear equations, A*b = c. While discussing the relative merits of the solving a system for a particular right hand side versus solving for the inverse matrix, I made the assertion that it is faster to solve a particular system than it
The SAS/IML language provides two functions for solving a nonsingular nxn linear system A*x = c: The INV function numerically computes the inverse matrix, A-1. You can use this to solve for x: Ainv = inv(A); x = Ainv*c;. The SOLVE function numerically computes the particular solution, x, for a
I've previously discussed how to find the root of a univariate function. This article describes how to find the root (zero) of a function of several variables by using Newton's method. There have been many papers, books, and dissertations written on the topic of root-finding, so why am I blogging
Recently I had to compute the trace of a product of square matrices. That is, I had two large nxn matrices, A and B, and I needed to compute the quantity trace(A*B). Furthermore, I was going to compute this quantity thousands of times for various A and B as part
Both covariance matrices and correlation matrices are used frequently in multivariate statistics. You can easily compute covariance and correlation matrices from data by using SAS software. However, sometimes you are given a covariance matrix, but your numerical technique requires a correlation matrix. Other times you are given a correlation matrix,
